Лекции по метрологии / Лекция №9

Лекция №9

Грубые погрешности и методы их исключения.

Грубая погрешность или промах – это погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.

Источником грубых погрешностей нередко бывают резкие изменения условий измерения и ошибки, допущенные оператором.

Корректная статистическая обработка выборки возможна только при её однородности, т. е. в том случае, когда все её члены принадлежат к одной и той же генеральной совокупности. В противном случае обработка данных бессмысленна.

Существует ряд критериев для оценки промахов.

Критерий 3σ. В этом случае считается, что результат, возникающий вероятностью , малореален и его можно квалифицировать промахом, т. е. сомнительный результат отбрасывается, если

.

Величины и σ вычисляют без учета .

Данный критерий надежен при числе измерений .

Если число измерений не велико (до 10), то можно использовать критерий Шовине. В этом случае промахом считается результат , если разность превышает значения σ, приведенные ниже в зависимости от числа измерений:

Методы обработки результатов измерений.

1. Многократные прямые равноточные измерения.

Равноточными называют измерения, которые проводятся средствами измерений одинаковой точности по одной и той же методике при неизменных внешних условиях.

Последовательность обработки результатов измерений включает следующие этапы:

• Исправляют результаты наблюдений исключением (если это возможно) систематической погрешности;

• Вычисляют среднее арифметическое значение ;

• Вычисляют выборочное с.к.о. от значения погрешности измерений;

• Исключают промахи;

• Определяют закон распределения случайной составляющей;

• При заданном значении доверительной вероятности Р и числе измерений n по таблицам определяют коэффициент Стьюдента ;

• Находят границы доверительного интервала для случайной погрешности ;

• Если величина сравнима с абсолютным значением погрешности СИ, то величину считают неисключенной системататической составляющей и в качестве доверительного интервала вычисляют величину:

Если в результате измерительного эксперимента можно чётко выделить составляющие НСП, то определяется:

по приближенной формуле;

где ; - граница i – той составляющей НСП; к – коэффициент, определяемый принятой доверительной вероятностью Р.

• Окончательный результат записывается в виде:

, при вероятности Р.

2. Неравноточные измерения.

При планировании измерительных операций и обработке их результатов зачастую приходится пользоваться неравноточными измерениями (т. е. измерениями одной и той же физической величины, выполненными с различной точностью, разными приборами, в разных условиях, различными исследователями и т. п.).

Для оценки наиболее вероятного значения величины по данным неравноточных измерений вводят понятие «веса измерения»:

,

где и - объём и дисперсия i-й серии равноточных измерений.

Тогда, если неравноточные измерения привели к результатам ( - среднеарифметическое ряда равноточных измерений; ), то наиболее вероятным значением величины будет её средневзвешенное значение:

.

Вероятность Р того, что лежит в пределах равноточных измерений , определяется вышеприведенным методом для равноточных измерений.

3. Однократные измерения.

Прямые статистические измерения в большей степени относятся к лабораторным (статистическим).

Для производственных процессов более характерны однократные технические прямые или косвенные измерения. Здесь процедура измерений регламентируется заранее, с тем чтобы при известной точности СИ и условиях измерения погрешность не превзошла определённое значение, т. е. значения и Р заданы априори. Поскольку измерения выполняются без повторных наблюдений, то нельзя отделить случайную от систематической составляющей погрешности. Поэтому для оценки погрешности дают лишь её границы с учетом возможных влияющих величин. Последние лишь оценивают своими границами, но не измеряют.

В принципе, однократные измерения достаточны, если неисключенная систематическая погрешность (например, класс точности СИ) заведомо больше случайной. Практически это достигается при . Тогда результат измерения записывают в виде:

, при вероятности Р=0,95,

где - результат, зафиксированный СИ;

- суммарная погрешность измерения, определяемая классом точности СИ и методической погрешностью.

Пример. Оценить погрешность результата однократного измерения напряжения U=0,9 В на входном сопротивлении R=4 Ом, выполненного вольтметром класса точности 0,5 с верхним пределом диапазона измерений U_N=1,5 В и имеющим сопротивление R_v=1000 Ом. Известно, что дополнительные погрешности показаний СИ из-за влияния магнитного поля и температуры не превышают соответственно и допускаемой предельной погрешности.

Решение.

1. Предел допускаемой относительной погрешности вольтметра на отметке 0,9 В составляет:

.

Действительно:

2. При подсоединении вольтметра исходное напряжение изменяется из-за наличия и составит:

.

Тогда методическая погрешность, обусловленная конечным значением , в относительной форме составит:

.

3. Данная методическая погрешность является систематической составляющей погрешностью измерения и должна быть внесена в результат в виде поправки или в абсолютной форме на отметке 0,9 В:

Тогда результат измерения с учетом поправки будет равен:

.

4. Поскольку основная и дополнительные погрешности заданы своими граничными значениями, то они могут рассматриваться как неисключенные систематические.

При доверительной вероятности Р=0,95 доверительная граница неисключенной систематической составляющей будет:

.

Для Р=0,95 к=1,1.

А абсолютной форме:

.

5. В виду того, что , окончательный результат измерения записывается в виде:

.

4. Косвенные измерения.

Косвенные измерения предполагают наличие функциональной связи:

,

где - подлежащие прямым измерениям аргументы функции .

Очевидно, что погрешность в оценке зависит от погрешностей при измерениях аргументов.

Косвенные измерения при линейной зависимости между аргументами.

В этом случае:

;

где - постоянные коэффициенты.

Предполагается, что корреляция между погрешностями измерений отсутствует. Результат измерения вычисляют по формуле:

;

где - результат измерения с введенными поправками.

Оценку с.к.о. результата измерений вычисляют по формуле:

,

где - оценка с.к.о. результата измерений .

Доверительные границы случайной погрешности при нормальном распределении погрешностей вычисляют по формуле:

,

где - коэффициент Стьюдента, соответствующей доверительной вероятности Р и эффективному числу наблюдений – m.

,

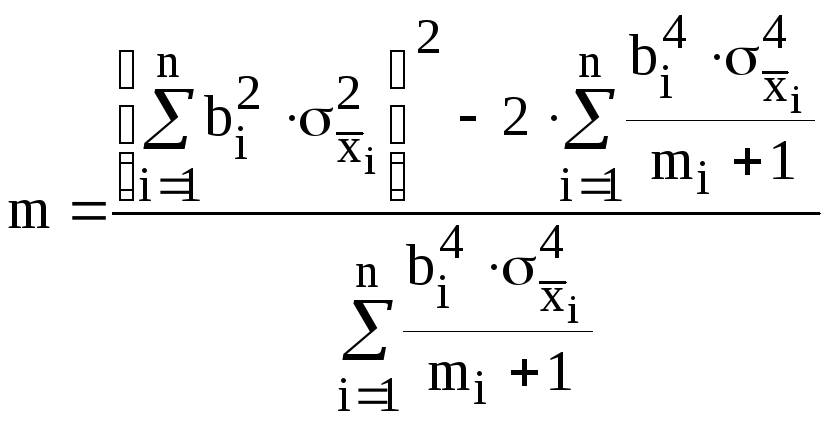где - число наблюдений при измерении .

При наличии корреляционной связи между аргументами с.к.о. результата косвенного измерения, с.к.о. рассчитывают по формуле:

.

Здесь - несмещенная оценка корреляции между погрешностями аргументов и :

,

где - i-е результаты прямых измерений k-го и l-го аргументов, m – число прямых измерений аргументов.

Корреляция между аргументами чаще всего возникает в тех случаях, когда их измерения проводятся одновременно и подвергаются одинаковому влиянию внешних условий (температуры, влажности, напряжению питающей сети, помех и т. п.).

Косвенные измерения при нелинейной зависимости.

При некоррелированных погрешностях измерений используется метод линеаризации путем разложения функции в ряд Тейлора:

,

где - отклонение отдельного результата наблюдения от ; - остаточный член разложения.

Остаточным членом пренебрегают, если:

,

,

где - оценка с.к.о. случайной погрешности результата измерения .

Результат измерения вычисляют по формуле:

.

Оценку с.к.о. случайной составляющей погрешности результата такого косвенного измерения вычисляют по формуле:

.

Доверительные границы:

.

Абсолютная погрешность косвенного измерения равна:

.

Пример.

Получить выражение для расчета абсолютной погрешности плотности твердого тела.

- формула для определения плотности.

Здесь - масса и объём твердого тела.

- оценки массы и объёма, полученные в результате опыта.

Разложим в ряд Тейлора это выражение в окрестности точки :

.

Пренебрегая остаточным членом и учитывая, что

;

,

получим:

.