Лекции по метрологии / Лекция №14

Лекция № 14

Классы точности средств измерений.

Класс точности – это обобщенная метрологическая характеристика СИ.

Рассмотрим, как формируются классы точности.

1. Рассмотрим СИ имеющие только аддитивную погрешность.

Вспомним, что аддитивная погрешность не зависит от измеряемой величины.

Графически это можно представить следующим образом:

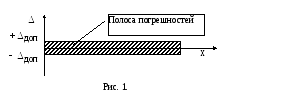
Т. е. погрешность СИ в основном находится в полосе, ограниченной прямыми параллельными оси абсцисс .

Здесь - максимально допустимая погрешность СИ.

Иными словами, погрешность лежит в этой полосе, но возможны случаи, когда погрешность и выходит из этой полосы, но это событие практически невозможно.

Структурную схему такого прибора (т. е. прибора, имеющего аддитивную погрешность) можно представить следующим образом:

Здесь:

x – измеряемая физическая величина (входная величина), неслучайная величина;

Y – выходная величина СИ (это может быть показание – стрелка, табло, либо сигнал измерительной информации – ток, напряжение и т. п.) с учетом помехи измерения, т. е. случайная величина;

y - выходная величина СИ без учета помехи измерения (истинное значение), неслучайная величина;

f – аддитивная помеха, за счет которой и возникает погрешность измерения, случайная величина;

K – коэффициент передачи СИ, const.

.

Мы рассматриваем измерения в статике, т. е. когда входная величина x не изменяется во времени. Поэтому СИ можно охарактеризовать коэффициентом К.

Для простоты:

K=const.

Помеха f является в общем случае случайной величиной (с. в.).

Как и любую с. в. помеху f можно охарактеризовать следующими характеристиками:

• Математическое ожидание

;

Если , это означает, что СИ имеет систематическую погрешность и её необходимо исключить из результатов измерения (коррекцией самого прибора);

• С.к.о.

.

Запишем уравнение, связывающее выходную величину СИ с входной:

.

Определим погрешность измерения:

;

т. е. погрешность - это с. в. Она не зависит от измеряемой величины x.

Как и любая с. в. характеризуется:

;

.

Для определения полосы погрешности необходимо определить .

Для этого необходимо знание закона распределения с. в. (или f).

Зная закон распределения и задаваясь доверительной вероятностью Р (Р=0,9 и больше, в основном Р=0,95) определяем квантильный множитель и далее доверительный интервал:

это абсолютная допустимая погрешность (аддитивная).

Для таких СИ класс точности определяется через относительную приведенную погрешность:

,

где - истинное значение выходной величины (нормирующее значение, равное конечному значению, т. е. максимальному значению).

Значение выбирается из ряда предпочтительных чисел:

;

где А=1; 1,5; (1,6); 2; 2,5; (3); 4; 5; 6,

1,6; 3 – допускаются, но не рекомендуются; n=1; 0; - 1; - 2; …

Класс точности обозначается для данной погрешности:

0,5.

Определим погрешность через с.к.о.:

;

т. е.

.

Здесь:

- относительное с.к.о. аддитивной погрешности.

2. Рассмотрим СИ имеющее только мультипликативную погрешность.

Вспомним, что мультипликативная погрешность линейно зависит от измеряемой величины.

Графически это можно представить следующим образом.

Структурную схему такого прибора можно представить следующим образом.

Здесь - случайная величина, изменяющая коэффициент передачи.

Величина имеет следующие характеристики:

;

.

Запишем уравнение связи:

.

Определим погрешность измерения:

.

Случайная величина имеет следующие характеристики:

;

.

Необходимо определить .

Определяем квантильный множитель и далее допустимую погрешность отклонения.

.

Это абсолютная допустимая погрешность (мультипликативная).

Для таких СИ класс точности определяется через относительную погрешность:

.

Значение определяется из того же ряда предпочтительных чисел.

Обозначение класса точности таких СИ несколько отличается. Например:

Отметим особенность такого определения класса точности:

.

Т. е. не зависит от измеряемой величины, в отличие от абсолютной погрешности.

Обозначим:

- относительное с.к.о. мультипликативной погрешности.

Тогда относительную погрешность можно представить в следующем виде:

.

3. Рассмотрим СИ имеющее как аддитивную, так и мультипликативную составляющие погрешности.

Структурную схему такого СИ можно представить следующим образом.

Запишем уравнение связи:

.

Определим погрешность измерения:

.

Случайная погрешность имеет следующие характеристики:

.

Найдем дисперсию с. в. .

Для этого вспомним, что дисперсия суммы случайных независимых величин равна сумме дисперсий этих величин.

.

Тогда с.к.о. этой величины:

.

Определим .

Аналогично, как и ранее:

.

Построим график этой погрешности.

Как видно из графика, нелинейно зависит от x.

На практике эту зависимость аппроксимируют следующим образом.

Введем обозначения.

- погрешность начала диапазона измерений (х=0):

- погрешность конца диапазона измерений (x=x_к=x_N).

Тогда аппроксимирующую зависимость можно представить следующим образом.

.

Эта зависимость представлена на рис. 6 прямой линией.

Преобразуем эту зависимость к следующему виду.

.

Найдем относительную погрешность.

.

Введем следующие обозначения.

.

Т.е.

- приведенная погрешность СИ для начала диапазона измерения.

.

Т. е.

- приведенная погрешность СИ для конца диапазона измерения.

Тогда относительную погрешность можно представить в следующем виде:

.

Для таких приборов класс точности нормируется в следующем виде:

.

Например: .

Отсюда , , а относительная погрешность СИ запишется в виде:

.

Рассмотрим конкретный пример на применение класса точности для оценки погрешностей измерения.

Пример.

Отчет по шкале прибора с пределами измерений 0-50 А и равномерной шкалой составил 25 А. Пренебрегая другими видами погрешностей измерения, оценить пределы допускаемой абсолютной погрешности этого отсчета при использовании различных СИ классов точности: 0,5; ; .

Решение.

1. Для СИ класса точности 0,5.

.

.

.

.

2. Для СИ класса точности

.

.

.

.

3. Для СИ класса точности .

.

.

.

.

С другой стороны:

.

Отсюда

.