Лекции.Сопромат / Лекция 4

Л е к ц и я 4

ОСНОВЫ РАСЧЕТА ТИПОВЫХ ЭЛЕМЕНТОВ,

РАБОТАЮЩИХ НА РАСТЯЖЕНИЕ, КРУЧЕНИЕ И ИЗГИБ.

СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ

Определение напряжений и расчет на прочность при плоском чистом изгибе. Расчет на прочность при плоском поперечном изгибе. Расчет статически неопределимых систем, работающих на растяжение.

Определение напряжений и расчет

на прочность при плоском чистом изгибе

При изгибе происходит искривление оси стержня. Продольные волокна, расположенные на выпуклой стороне стержня, растягиваются, а на вогнутой стороне – сжимаются. Слой, разделяющий области растяжения и сжатия и не испытывающий деформаций, называется нейтральным. Линия пересечения нейтрального слоя с плоскостью поперечного сечения называется нейтральной линией. Нейтральная линия перпендикулярна плоскости изгиба. Примем, что плоскости изгиба и внешних сил совпадают с плоскостью YZ, а нейтральная линия – с осью X (рис. 4.1).

В результате растяжения (сжатия) продольных волокон в поперечном сечении стержня при изгибе возникают нормальные напряжения σ, равнодействующей которых является изгибающий момент M. При определении нормальных напряжений используются гипотеза плоских сечений и гипотеза об отсутствии надавливания продольных слоёв стержня друг на друга.

Рассмотрим деформирование элемента стержня длиной dz (рис. 4.2). Ввиду малости деформаций продольные волокна, являющиеся в деформированном состоянии частями окружностей, изображены в виде прямых отрезков.

Деформация волокна ab, расположенного на расстоянии y от нейтрального слоя, равна

где ρ – радиус кривизны нейтрального слоя;

(4.1)

Используя закон Гука (3.1) и (4.1), находим

(4.2)

Изгибающие моменты в сечении при изгибе в плоскости YZ связаны с нормальными напряжениями зависимостями (рис. 4.3)

(4.3)

(4.4)

Из (4.3) и (4.2) получаем

(4.5)

Выразив из (4.5) отношение и подставив в (4.2), будем иметь

(4.6)

При изгибе продольная сила в сечении равна нулю. Из данного факта и формул (3.4) и (4.2) находим

Это означает, что ось X (нейтральная линия) является центральной осью сечения ( проходит через центр тяжести сечения). Отсюда следует, что ρ представляет собой радиус кривизны изогнутой оси стержня.

Из соотношений (4.4) и (4.2) получаем

Д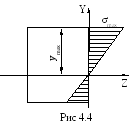анный результат показывает, что оси X и Y являются главными осями сечения.

Согласно формуле (4.6), эпюра нормального напряжения при изгибе имеет вид (рис. 4.4). Из эпюры следует, что максимальное напряжение возникает в точках, наиболее удаленных от оси стержня

(4.7)

Если стержень имеет постоянное по длине поперечное сечение, то опасным является сечение, в котором действует максимальный изгибающий момент. В этом случае условие прочности при изгибе имеет вид

(4.8)

Расчет на прочность при плоском поперечном изгибе

При поперечном изгибе в поперечном сечении стержня возникают и нормальные и касательные напряжения. В результате действия касательных напряжений поперечные сечения искривляются, а продольные волокна оказывают давление друг на друга. Использование в данном случае формулы (4.6) будет приводить к ошибке Δσ. Можно показать, что

где k₁, k₂ – коэффициенты пропорциональности;

h, l – высота и ширина поперечного сечения балки.

Для большинства балок . Поэтому ошибкой Δσ и касательными напряжениями можно пренебречь, а расчет на прочность выполнять с использование условия (4.8), полученного для чистого изгиба.

Расчет статически неопределимых систем,

работающих на растяжение.

Система, состоящая из стержней, соединенных между собой в единую конструкцию, называется стержневой. Будем рассматривать стержневые системы, стержни которых соединены между собой по краям шарнирами. Шарнирные соединения стержней называются узлами системы. При действии внешней нагрузки в узлах системы стержни будут испытывать деформацию растяжения или сжатия (в дальнейшем эту деформацию будем называть растяжением).

При растяжении в поперечном сечении стержня возникают нормальные напряжения, которые равномерно распределены по плоскости сечения и определяются по формуле (3.6)

В результате растяжения происходит изменение длины стержня. Абсолютная деформация (удлинение или укорочение) стержня вычисляется по формуле

(4.9)

где l – длина стержня; Е – модуль Юнга материала стержня.

Произведение ЕА называется жесткостью стержня при растяжении. Если продольная сила и жесткость не изменяются по длине стержня, то (4.2) принимает вид

(4.10)

Стержневая система может быть статически определимой и статически неопределимой. Если с использованием уравнений равновесия и метода сечений можно определить реакции опор и продольные усилия в стержнях, то система называется статически определимой. В статически неопределимых системах найти из уравнений равновесия все неизвестные параметры нельзя. Разность между числом неизвестных величин и числом уравнений равновесия, которые можно составить для системы, называется степенью статической неопределимости n

(4.11)

где n₁ – число неизвестных параметров; n₂ – число возможных уравнений равновесия.

Для расчета статически неопределимых систем в дополнение к уравнениям равновесия необходимо составить n соотношений между абсолютными деформациями стержней, которые называются уравнениями совместности деформаций. После этого, используя (4.10), преобразовать эти уравнения в дополнительные соотношения между внутренними силами. Неизвестные параметры находятся в результате решения системы, состоящей из уравнений равновесия и n дополнительных уравнений связи между внутренними силами. Для того, чтобы составить уравнения совместности деформаций, необходимо рассмотреть одно из возможных деформированных состояний системы.

Определение продольных сил в статической неопределимой системе, работающей на растяжение (сжатие), выполняется в следующей последовательности.

1. Разрезать стержни системы плоскостями, перпендикулярными к осям стержней. В результате этого система будет разделена на несколько частей. Отбросить части системы, не содержащие внешней нагрузки. Заменить отброшенные части стержня неизвестными продольными силами. Полученная схема называется схемой сил. По формуле (4.11) определить степень статической неопределимости системы.

2. Изобразить одно из возможных деформированных состояний системы, допускаемое внешними связями и упругими свойствами стержней. Полученная схема называется схемой деформаций. Схема деформаций может не соответствовать внешней нагрузке. Из схемы деформаций получить n уравнений совместности деформаций. Используя (4.10), из уравнений совместности деформаций найти n дополнительных уравнений связи между продольными силами.

3. Выполнить проверку и при необходимости корректировку схемы сил. Необходимо проверить, что если на схеме деформаций стержень растянут, то на схеме сил на него действует продольная сила, соответствующая растяжению. В том случае, когда на схеме деформаций стержень сжат, на схеме сил на него должна действовать продольная сила, соответствующая сжатию.

4. Используя схему сил, составить уравнения равновесия. Решив систему, состоящую из уравнений равновесия и дополнительных уравнений связи между продольными силами, определить значения продольных сил.

Пример

Жёсткий брус AD прикреплен к неподвижной шарнирной опоре A и двум упругим стержням 1 и 2, имеющим площадь поперечного сечения A (рис 4.5). Определить продольные усилия в стержнях N₁ и N₂.

1. Разрезаем стержни 1 и 2 плоскостями, перпендикулярными к их осям, и оставляем нижнюю часть системы, содержащую шарнир A (рис. 4.6). Действие верхней отброшенной части заменяем продольными силами N₁ и N₂. Для определения четырех неизвестных X, Y, N₁ и N₂ можно составить три уравнения равновесия. Степень статической неопределимости данной системы равна

2. Наложенные на брус AD связи разрешают его поворот относительно шарнира A. Изображаем схему деформаций системы (рис. 4.7). Ввиду малости упругих деформаций на рис. 4.Х перемещения точек B и C по дуге заменены на перемещения по касательной к дуге. Составляем уравнение совместности деформаций

Применяя соотношение (4.11), получаем дополнительное уравнение взаимосвязи между продольными силами

(4.12)

3. Выполняем проверку схемы сил. На схеме деформаций стержни 1 и 2 растянуты. Поэтому на схеме сил изображены продольные усилия N₁ и N₂, соответствующие растяжению.

4. Используя схему сил, составляем уравнения равновесия. Так как по условию задачи не требуется определение реакций X и Y, то составляем одно уравнение в виде

(4.13)

Решая систему (4.12) и (4.13), получаем

5