4. Базис и ортогонализация системы векторов

4.1. Базисы системы векторов

Базисом системы векторов a₁, a₂, …, a_n называется такая ее часть b₁, b₂, …, b_r (каждый из векторов b_r является одним из векторов a₁, a₂, …, a_n), которая удовлетворяет следующим условиям:

1) b₁, b₂, …, b_r – линейно независимая система векторов;

2) любой вектор системы a₁, a₂, …, a_n разлагается по векторам b₁, b₂, …, b_r.

Замечание 1.

В линейном пространстве, вообще говоря, бесконечное множество базисов, но если пространство n-мерное, то число векторов в каждом базисе одно и то же и равно n.

Замечание 2.

Если к любому базису добавить ненулевой вектор, то мы получим уже линейно зависимую систему.

Замечание 3.

Если диагональная система векторов является частью системы m–мерных векторов a₁, a₂,…,a_n, то диагональная система является базисом системы векторов.

Замечание 4.

Каждую линейно независимую часть a₁, a₂, …, a_к системы векторов можно дополнить до базиса этой системы.

Замечание 5.

Каждый вектор системы a₁, a₂, …, a_n единственным образом разлагается по векторам ее базиса.

Теорема. Пусть дана система векторов a₁, a₂,…, a_n.

Рассмотрим систему уравнений

a₁x₁+a₂x₂+…+a_nx_n=0

и ее общее решение

a₁^'x₁+a₂^'x₂ +…+a_n^'x_n=0.

Тогда:

1) векторы, соответствующие диагональной части системы a₁^', a₂^', …, a_n^', образуют базис системы векторов a₁, a₂, …, a_n.

2) вектор a_j разлагается по найденному в первом пункте базису с теми же координатами, с которыми вектор a_j^' разлагается по диагональной части системы a₁^', a₂^', …, a_n^'.

Данная теорема позволяет сформулировать алгоритм построения базиса данной системы векторов a₁, a₂,…, a_n:

1) выписать систему уравнений

a₁x₁+a₂x₂+…+a_nx_n=0

и методом Гаусса найти ее общее решение

a₁^'x₁+a₂^'x₂ +…+a_n^'x_n=0;

2) найти диагональную часть системы векторов a₁^', a₂^', …, a_n^';

3) векторы системы a₁, a₂, …, a_n, соответствующие диагональной части системы a₁^', a₂^', …, a_n^', образуют базис данной системы векторов a₁, a₂, …, a_n.

Пример. Найти базис системы векторов

a₁ = (1, 1, 2), a₂ = (3, 1, 2), a₃ = (1, 2, 1), a₄ = (2, 1, 2)

и все векторы разложить по базису.

Рассмотрим систему уравнений

a₁x₁ + a₂x₂ + a₃x₃ + a₄x₄ = 0

и методом Гаусса найдём её решение

(-1) (-2)

x1	x2	x3	x4
1	3	1	2
1	1	2	1
2	2	1	2
1	3	1	2
0	-2	1	-1
0	-4	-1	-2
1	3	1	2
0	1	-0.5	0 (-3) (4) .5
0	-4	-1	-2
1	0	2.5	0.5
0	1	-0.5	0.5
0	0	-3	0
1	0	2.5	0.5
0	1	-0.5	0.5
0	0	1	0 (0.5) (-2.5)
1	0	0	0.5
0	1	0	0.5
0	0	1	0

Общее решение системы имеет вид:

a₁^'x₁+a₂^'x₂ +a₃^'x₃+a₄^'x₄=0,

; ;;,

где a^'₁, a^'₂ и a^'₃ образуют диагональную систему векторов, следовательно, a₁, a₂ и a₃ являются базисом системы векторов a₁, a₂, a₃, a₄.

Разложим теперь a₄ по базису a₁, a₂, a_3.

Для этого сначала разложим соответствующий вектор a^'₄ по диагональной системе a^'₁, a^'₂, a^'₃, имея в виду, что коэффициентами разложения векторов по диагональной системе являются их координаты:

Вектор a₄ разлагается по базису a₁, a₂ и a₃ с теми же коэффициентами, что и вектор a^'₄.

a₄=0,5 a₁+0,5 a₂+0 a₃.

Вектор a^'₁ разлагается по диагональной системе a^'₁, a^'₂, a^'₃ следующим образом

a₁=1 a₁+0 a₂+0 a₃

Вектор a₁ разлагается по базису a₁, a₂ и a₃ с теми же коэффициентами, что и вектор a^'₁.

a₁=1 a₁+0 a₂+0 a₃

Векторы a₂, и a₃ разлагаются аналогично.

Пример. Найти базис системы векторов

a₁ = (5, 2, -3, 1); a₂ = (4, 1, -2, 9); a₃ = (1, 1, -1, 2);

a₄ = (3, 4, -1, 2); a₅=(13, 8, -7, 4)

и все векторы, не вошедшие в базис, разложить по базису.

Рассмотрим систему уравнений

a₁x₁ + a₂x₂ + a₃x₃ + a₄x₄ + a₅x₅ = 0

и методом Гаусса найдём её решение

(-11) (3) (-5)

(3)

X1	X2	X3	X4	X5
5	4	1	3	1 (-1) (1) (2) 3
2	1	1	4	8
-3	-2	-1	-1	-7
1	3	-2	2	4
5	4	1	3	13
-3	-3	0	1	-5
2	2	0	2	6
11	11	0	8	30
0	-1	1	-2	-2
0	0	0	4	4
1	1	0	1	3
0	0	0	-3	-3
0	-1	1	0	0
0 (2) (-1)	0	0	1	1
1	1	0	0	2

Так как после выполнения преобразований система не содержит 4 уравнения, она является разрешенной.

Общее решение системы имеет вид:

a₁^'x₁+a₂^'x₂ +a₃^'x₃+a₄^'x₄+a₅^'x₅=0,

где

; ;;;

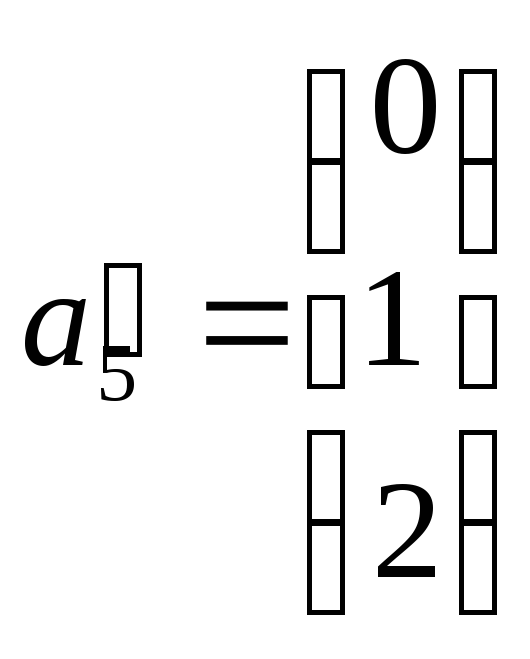
где a^'₁, a^'₃ и a^'₄ образуют диагональную систему векторов, следовательно, a₁, a₃ и a₄ являются базисом векторов a₁, a₂, a₃, a₄, a₅.

Разложим теперь a₂ и a₅ по базису a₁, a₃, a_4.

Для этого сначала разложим соответствующие вектора a^'₂ и a^'₅ по диагональной системе a^'₁, a^'₃, a^'₄, имея в виду, что коэффициентами разложения векторов по диагональной системе являются их координаты:

Вектора a₂ и a₅ разлагается по базису a₁, a₂ и a₄ с теми же коэффициентами, что и вектора a^'₂ и a^'₅.

a₂=a₁–a₃; a₅=2a₁+a₄