2.5. Разложение вектора по системе векторов

Пусть дана система n -мерных векторов выбираемn – произвольных чисел .

Вектор называетсялинейной комбинацией векторов с коэффициентами.

Пусть теперь наряду с векторами дан ещеn-мерный вектор . Будем говорить, что векторлинейно выражается через векторы, если он равен некоторой линейной комбинации векторов, т.е. найдется такой набор чисел, что

. (5)

В этом случае будем говорить также, что вектор разлагается по векторам. Числаназываются коэффициентами разложения векторапо системе.

Разложение считается отличным от разложения (5), если различна хотя бы одна пара соответствующих коэффициентов разложения (т.е. хотя бы один).

Справедливы следующие утверждения:

1. Нулевой вектор разлагается по каждой системе векторов

.

2. Если вектор разлагается по части системы векторов, то он разлагается и по всей системе векторов.

Предположим, что

, где ,

тогда .

3. Каждый -мерный векторразлагается по диагональной системе- мерных векторов:

с коэффициентами, которые равны координатам вектора .

В самом деле

.

4. Если вектор разлагается по системе векторов, а каждый вектор этой системы разлагается по системе векторов, то векторразлагается по системе векторов.

Из условия следует, что

После подстановки получаем:

Т.е. вектор разлагается по векторам.

2.6. Векторная форма записи системы линейных уравнений

Используя введенные операции над векторами, запишем систему линейных уравнений:

(1)

в векторной форме. Обозначим столбцы коэффициентов при неизвестных

, ,…,;.

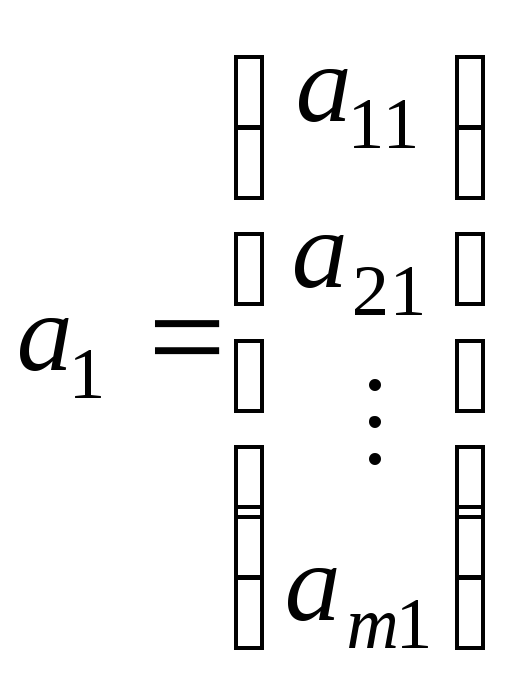Тогда систему (1) можно представить в виде:

(2)

Уравнение (2) называется векторной формой системы линейных уравнений (1).

Последовательность чисел называют решением системы (2), если– верное векторное равенство.

Пусть n-мерный вектор () является решением системы (1). Тогда ясно, что для разложения векторапо системедостаточно найти решение системы линейных уравнений (2).

Пример. Дана система векторов и вектор

;;;;.

Пример. Выяснить разлагается ли вектор по системе векторов.

Для этого необходимо решить систему уравнений

.

Имеем:

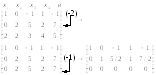
Получили систему уравнений:

,

которая эквивалентна исходной (т.е. имеет то же множество решений). Выразим главные неизвестные ичерез свободные.. Получим общее решение:

.

Достаточно положить свободным неизвестным ипроизвольные значения и получить разложение векторапо системе векторов.

Пример. , тогда,.

Следовательно:

.

Если же , тогда,

и .

2.7. Задания

1. Найти разложение вектора В по диагональной системе (упражнение 1).

2. Найти разложение вектора В по системе А1, А2, А3 (упражнение 2).

3. Найти разложение вектора В по векторам А1, А2, А3 (упражнение 3).

4. Разложить каждый вектор системы А1, А2, …, Аn по векторам этой системы.

5. Доказать, что если векторы В1 и В2 разлагаются по системе векторов А1, А2, …, Аn, то векторы В1+В2, kB1, t1B1+t2B2 также разлагаются по системе векторов А1, А2, …, Аn (k, t1, t2 – константы).

6. Вектор В разлагается по системе векторов А1, А2, …, Аm. Доказать, что каждый вектор системы В+А1, В+А2,…, В+Аm разлагается по системе А1, А2, …, Аm.

Упражнения 1, 2, 3 выполняются по вариантам, остальные – без вариантов.

Таблица 1

№ варианта	Векторы А1, А2, А3, В
	Упражнение 1	Упражнение 2		Упражнение 3
	В	A1 A2 A3	B	A1 A2 A3	B
	7 5 -3 4	0 0 1 1 0 1 0 1 1	1 3 0	-1 -1 0 2 2 2 8 2 1 2 1 2	1 1 1 4
	-2 0 3 1	1 0 1 0 1 0 1 1 0	-2 1 1	-3 -1 5 5 2 3 5 2 1 2 1 2	-5 5 1 4
	5 6 -3 2	1 -1 1 0 2 0 -2 2 0	0 4 1	-2 -2 -2 0 2 3 0 2 1 2 1 2	-3 3 1 4
	-5 7 -1 0	1 -1 1 0 1 0 -2 1 0	0 4 1	-1 0 -4 3 2 3 0 2 1 2 1 2	-2 3 1 4

Окончание таблицы 1

№ варианта	Векторы А1, А2, А3, В
	Упражнение 1	Упражнение 2		Упражнение 3
	В	A1 A2 A3	B	A1 A2 A3	B
	4 -5 1 1	1 0 1 1 1 1 0 1 1	-2 5 1	-1 0 0 1 2 5 1 2 1 2 1 2	0 4 2 4
	9 -10 3 1	1 0 1 0 0 1 0 1 0	-8 4 6	-1 0 0 1 2 3 0 2 1 2 1 2	0 1 2 4
	0 5 -12 8	1 0 1 1 1 2 0 1 0	0 6 2	-1 -1 -2 0 2 3 0 2 1 2 1 2	-3 3 1 4
	9 -10 3 1	1 0 1 0 0 1 0 1 0	-8 4 6	-1 0 0 1 2 3 0 2 1 2 1 2	0 1 2 4
	1 2 -3 7	1 0 1 1 2 2 1 2 0	0 2 4	4 2 0 0 2 3 0 0 1 3 0 0	0 0 1 1
	0 0 -1 8	1 0 1 1 1 3 0 1 3	-1 1 2	-1 0 0 0 0 2 2 0 2 2 1 0 3 1 2 1	0 3 1 4
	-3 5 5 -4	2 0 1 1 4 2 0 5 0	6 6 0	-1 0 -2 0 2 3 0 2 2 2 1 2	-3 3 2 4
	-2 0 -5 -1	5 0 1 1 4 3 0 5 1	10 2 0	1 4 4 0 1 3 2 1 4 0 1 0	-1 2 1 1
	5 -6 -1 4	3 0 1 2 1 1 0 1 0	-1 0 2	-2 1 -2 0 1 2 0 2 3 2 2 1	0 2 1 1