2.N-мерные векторы

2.1. Линейные операции надn-мерными векторами

В геометрии векторомв пространстве называется направленный отрезок. В фиксированной системе координат каждый вектораоднозначно определяется своими координатами:

, (1)

где называются координатами вектораa.

Если – какой-либо другой вектор, то

(2)

, (3)

где – число.

Сложение векторов и умножение вектора на число называются линейными операциями над векторами.

Обобщим понятие вектора следующим образом: назовем последовательность n чисел n-мерным вектором. Число называется первой координатой вектора;– второй координатой и т.д., а числоn (количество координат) называется размерностью вектора а.

Если ,, то

, .

Два n-мерных вектора:

, ,

считаются равными только тогда, когда равны их соответствующие координаты ,,…,.

Очевидно, что для любого вектора а:

, где .

Вектор называетсянулевым.

Вектор (-1)называетсяпротивоположным вектору и обозначается, т.е.. Ясно, чтои.

Так как операции над n-мерными векторами определяются через операции над их координатами, то свойства арифметических операций справедливы и для операций над векторами.

1. (сложение коммутативно).

2. (сложение ассоциативно).

3. ; (сложение дистрибутивно, где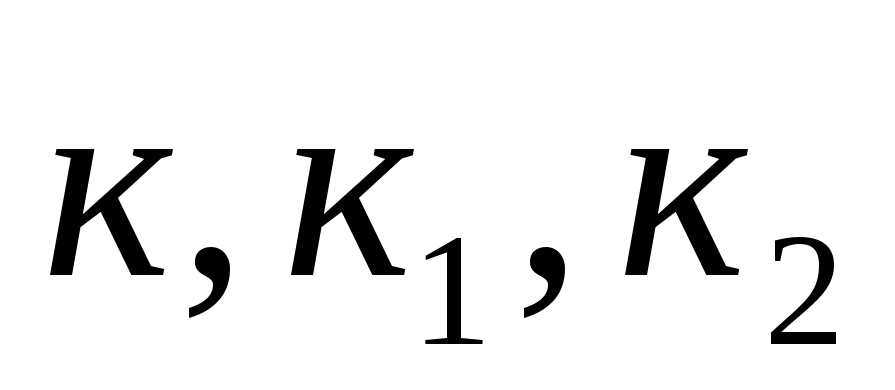– некоторые вещественные числа).

2.2. Скалярное произведение и длинаn-мерных векторов

Как известно из геометрии, если векторы а и заданы своими координатамии, то их скалярное произведениеопределяется по формуле:

.

По аналогии скалярным произведением n-мерных векторов ,называется число.

Некоторые свойства произведения чисел справедливы и для скалярного произведения векторов:

1. .

2. , гдечисло.

3. .

4. причемтогда и только тогда, когда(нулевой вектор).

Длиной n-мерного вектора называется число. Длина вектораобозначается.

Из 4-го свойства скалярного произведения векторов вытекает, что каждый -мерный векторобладает длиной, причем нулевой вектор, является единственным вектором, длина которого равна нулю.

Если а и в -мерные векторы, то справедливы следующие числовые соотношения:

1) ,-число

2) (неравенство Коши-Буняковского)

3)(неравенство треугольника)

Вектор называется нормированным, если его длина равна 1. Каждый вектор можно нормировать, т.е. умножить на число, чтобы векторбыл нормированным.

В самом деле:

,

.

2.3. Угол междуn-мерными векторами

Из неравенства Коши-Буняковского

следует

,

.

Углом между -мерными векторамииназывается значение; которое получается из решения уравнения:

(4)

и принадлежит отрезку .

Причем решение единственно при любых и. Следовательно, и угол между векторамииопределен однозначно.

Перепишем соотношение (4) в виде

,

отсюда следует, что скалярное произведение векторов и равно произведению длин этих векторов на косинус угла между ними.

Геометрическая характеристика векторов – длина вектора и угол между векторами – позволяет сформулировать критерий равенства n-мерных векторов.

Теорема. Ненулевые n-мерные вектора а и равны тогда и только тогда, когда угол между ними равен нулю и длины этих векторов равны.

2.4. Коллинеарные векторы

Два ненулевыхn - мерных вектора называются коллинеарными, если угол между ними равен 0 или .

Если а,в = 0, то коллинеарные векторы считаются одинаково направленными, если же ,то коллинеарные векторы противоположно направлены.

Символическая запись означает, что векторыа и одинаково (противоположно) направлены.

Ненулевые векторы а и в коллинеарны, тогда и только тогда, когда можно подобрать такое (число), что.