5. Ранг, транспонирование и след матрицы

5.1. Ранг матрицы

Пусть дана матрица:

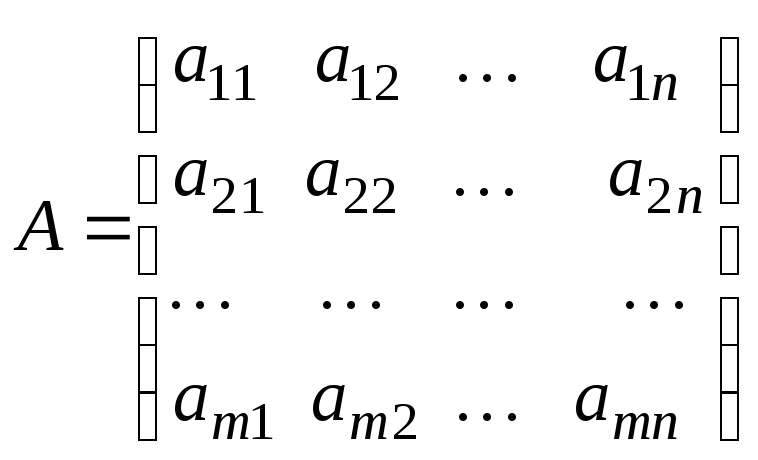
Минором kго порядка матрицы А назовем определитель матрицы с элементами, стоящими на пересечении выбранных k строк и k столбцов.

Минор обозначается так:

,

где i₁, i₂, ... i_k  номера выделенных строк;

j₁, j₂, ..., j_k  номера выделенных столбцов.

Пример:

1. .

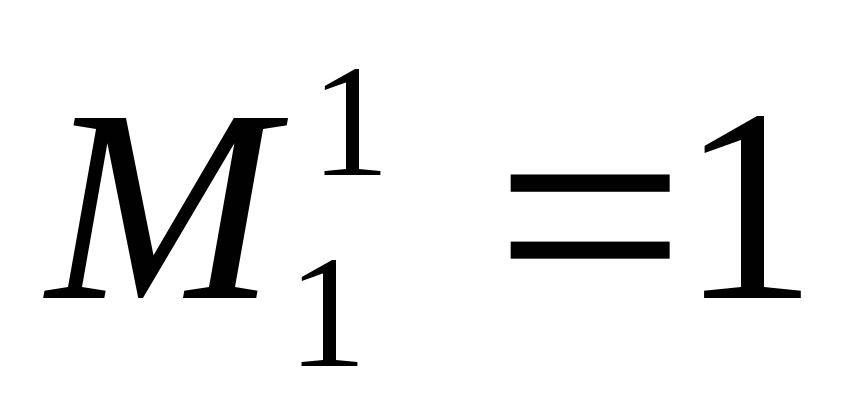2. Выпишем какой-нибудь минор второго порядка. Для этого выберем, например, 1-ю и 3-ю строки, 2-й и 4-й столбец.

3. Найдем какой-нибудь минор 3-го порядка. Для этого нужно выбрать все строки и какие-нибудь три столбца, например 2-й, 3-й и 4-й.

Получим минор:

*знак «–» означает, что 2 строки в определителе переставлены местами.

Минор называется невырожденным, если его определитель не равен нулю.

В нашем примере миноры невырожденные.

Рангом матрицы А называется наивысший порядок невырожденных миноров матрицы (обозначается rang A).

В нашем примере rang A=3, так как мы нашли невырожденный минор третьего порядка, а миноров четвертого порядка у нашей матрицы нет. Любой невырожденный минор порядка rang A называется базисным.

Для базисного минора выполняются следующие правила:

1. Столбцы, входящие в базисный минор, линейно независимы, так как в противном случае какой-то столбец из нашего минора линейно выражался бы через остальные и тогда определитель минора равнялся бы нулю.

2. Столбцы, не входящие в базисный минор, линейно выражаются через базисы.

Эти утверждения справедливы и для строк матрицы.

Существуют разные способы определения ранга матрицы. Рассмотрим метод Гаусса определения ранга. Для этого рассмотрим элементарные преобразования:

1. перестановку строк (столбцов) матрицы;

2. умножение строк (столбцов) на константу  0;

3. прибавление к i-той строке (столбцу) j-той строки (столбца), умноженной (умноженного) на некоторое число;

4. вычеркивание из матрицы нулевых строк (столбцов).

Все эти преобразования не меняют ранга матрицы.

Метод Гаусса нахождения ранга матрицы заключается в следующем. С помощью элементарных преобразований приводим матрицу А к виду:

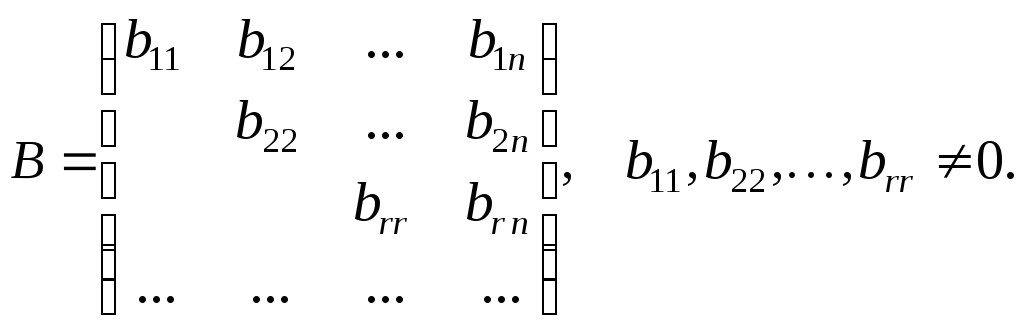
rang B = r.

Базисный минор – это минор

, rang A = rang B = 2.

Пример. Найти ранг матрицы

Решение.

rang A=2.

Рассмотрим систему уравнений система совместна тогда и только тогда, когда ранг матрицы этой системы равен рангу расширенной матрицы, т.е.

Можно доказать, что

Пример. Найти ранг и базисный минор матрицы А с помощью Mathcad.

1. Задаем системную переменную, вводящую нумерацию элементов массива с единицы.

2. Задаем элементы матрицы А.

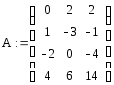
3. Задаем ранжированные переменные, определяющие изменение порядковых номеров строк (i) и столбцов (j) матрицы А.

4. Осуществляем линейные операции с элементами строк и столбцов матрицы А согласно методу Гаусса.

5. Дальнейшее преобразование бессмысленно. Ранг преобразованной матрицы А=2.

6. Осуществим проверку полученного результата с помощью встроенной функции MathCad rank().

7. Базисный минор матрицы А содержит 2 строки и 2 столбца. Его определитель не равен нулю.

5.2. Транспонирование матрицы

Пусть дана матрица:

Матрица A′=(a_ij′)_mn называется транспонированной к матрице A, если

.

Итак, чтобы получить матрицу A′_, нужно строки матрицы А сделать столбцами матрицы A′.

Пример