Все лабы по сопромату / ЛР4

Работа № 4

ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ ПЕРВОГО РОДА

Цель работы

1. Изучить экспериментальный метод определения упругих деформаций.

2. Экспериментально проверить закон Гука при растяжении.

3. Экспериментально определить для стали величину модуля Юнга.

Краткие теоретические сведения

Рассмотрим растяжение стержня под действием внешней центральной силы (рис.11).

Рис. 11. Схема растяжения стержня

Для определения напряжений в любом сечении применим метод сечений:

, .

Продольная сила является равнодействующей нормальных напряжений в поперечном сечении. Нормальные напряжения в нашем случае равномерно распределены по сечению, следовательно:

, т.к. получим .

. (7)

Зная напряжения (7) в поперечном сечении можно оценить прочность детали. Условие прочности при растяжении (сжатии) записывается в виде:

, (8)

где– допускаемые напряжения.

Определим деформации и перемещения при растяжении (рис. 12).

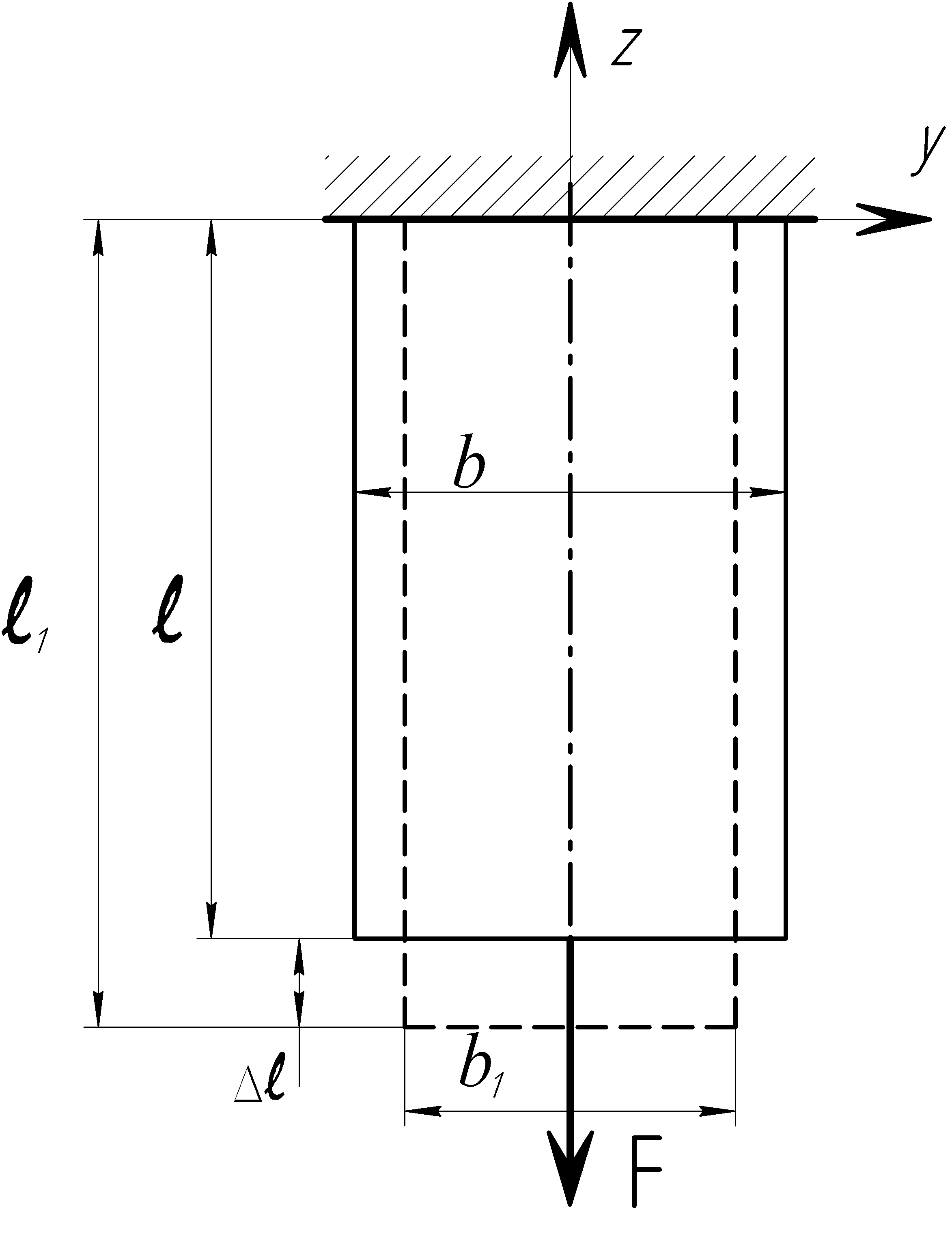
Рис. 12. Схема деформаций стержня.

- абсолютная продольная деформация,

- абсолютная поперечная деформация,

- относительная продольная деформация,

- относительная поперечная деформация.

Закон Гука при растяжении (сжатии): линейные деформации прямо пропорциональны нормальным напряжениям .

- модуль продольной упругости (модуль упругости первого рода).

Для стержня постоянного поперечного сечения:

.

Модуль упругости первого рода (модуль Юнга) является важнейшей упругой характеристикой конструкционных материалов. Он характеризует способность материала сопротивляться упругому деформированию и зависит от физических свойств материала. В законе Гука он является коэффициентом пропорциональности между действующей нагрузкой и упругими деформациями материала детали.

Закон Гука, выраженный через напряжение и относительную деформацию, имеет вид

.

Из этого соотношения ясен физический смысл модуля упругости. Его величина равна напряжению, при котором , а, следовательно, длина образца увеличивается вдвое. Это условие является воображаемым, т.к. кроме резины материалы не могут упруго деформироваться до такой большой степени.

Из относительной диаграммы растяжения (работа № 1) следует, что величина модуля упругости равна тангенсу угла наклона линейного участка диаграммы к оси деформаций . Для углеродистых и легированных сталей Е меняется в пределах 210⁵ – 2,210⁵ МПа.

Для экспериментального определения модуля Юнга необходимо располагать найденными из опыта на растяжение значениями напряжения и относительной деформации.

В качестве образца в данной работе используется брус с прямоугольным поперечным сечением.

Испытательная машина

Для испытаний используется универсальная машина УММ-5 с механическим приводом, которая развивает максимальное усилие 50 кн. Схема машины показана на рис.11. Образец 1 устанавливается в верхний 2 и нижний 3 захваты. Нижний захват перемещается с помощью ходового винта 4, который приводится во вращение двигателем 5 через коробку скоростей 6 и коническую пару 7. При движении захвата 3 вниз образец растягивается, а при движении вверх – сжимается. Переключениями в коробке 6 меняют скорость деформирования образца. Перемещение верхнего захвата 2 осуществляется вручную и служит для установки образца.

Рис. 13. Схема машины УММ-5

При испытании на растяжение движение нижнего захвата через образец 1, верхний захват 2 и систему рычагов 8 передается на маятниковый силоизмерительный механизм, принцип работы которого описан в работе № 1. Величина силы показывается на циферблате 9.

Движение нижнего захвата через тросик 10 преобразуется во вращение барабана 11, на котором намотана бумага для записи диаграммы растяжения. При растяжении образца перемещение верхнего захвата значительно меньше перемещения нижнего захвата. Поэтому угол поворота барабана пропорционален абсолютному удлинению образца.

В машине предусмотрена возможность перемещения нижнего захвата вручную с помощью рукоятки 13 и червячного редуктора 12.

Приборы для испытаний

Для измерения малых упругих деформаций в работе используются рычажные тензометры Гуггенбергера. Схема такого прибора показана на рис.12. Рамка 1 заканчивается внизу острой неподвижной ножкой 8. На рамке крепится шкала с ценой деления 0,001 мм. Подвижный рычажок 3 внизу жестко соединен с подвижной призматической ножкой 7, нижнее ребро которой врезается в образец, а верхнее опирается на треугольное гнездо рамки 1 (в точке А). В верхнем конце рамки шарнирно прикреплена стрелка 4. Она с помощью Т-образного хомутика 5 связана с верхним концом рычажка 3. Пружинка 6 стягивает это соединение. В месте прикрепления стрелки к рамке расположен винт, позволяющий регулировать начальное положение стрелки. Расстояние l между ножками называется базой тензометра – l=20 мм. С помощью специальной приставки база прибора может быть увеличена. Прибор прижимается к образцу с помощью специальной струбцинки.

Работает тензометр следующим образом. При деформировании образца расстояние между ножками (база) изменяется на величину , при этом подвижная ножка и связанный с ней рычажок 3 поворачиваются относительно т.А. Хомутик 5 толкает стрелку 4. Соотношение плеч элементов тензометра таково, что перемещение стрелки по шкале в 1000 раз больше .

В данной работе для получения точных результатов очень важно, чтобы растягивающая сила совпадала с осью образца. Даже небольшое внецентренное приложение нагрузки приводит к его дополнительному изгибу. Добиться высокой степени такой соосности практически очень трудно. Поэтому для полного исключения влияния внецентренного растяжения устанавливают два тензометра – на противоположных сторонах образца и используют среднее значение их показаний.

Порядок выполне6ния работы:

1. Измерить штангенциркулем с точностью 0,1 мм размеры поперечного сечения образца.

2. Установить с двух противоположных сторон образца два тензометра так, чтобы их база была ориентирована вдоль оси образца; мм.

3. Определить предельную нагрузку для образца:, где А – площадь поперечного сечения образца; МПа - предел текучести материала образца. Назначить допускаемую для образца нагрузку . Составить программу ступенчатого нагружения образца увеличивающейся силой с постоянным шагом до некоторого значения . Предусмотреть не менее пяти ступеней нагружения.

4. Для выборки люфтов во всей системе измерения начать не с нулевого значения силы, а с ее минимального значения, при котором показания тензометра нужно выставить на нуль.

5. Произвести ступенчатое нагружение образца, снимая показания силоизмерителя F и тензометров . Данные измерений занести в таблицу.

№ опыта	F		1-й тензометр		2-й тензометр
			мкм	мкм	мкм	мкм
	кГ	кН
1
2
3
4
5

6. Вычислить разности последующего и предыдущего показаний тензометров для каждой ступени нагружения и занести их в таблицу:

7. Вычислить средние значения разностей .

8. Вычислить среднее значение приращения абсолютного удлинения за одну ступень нагружения, выраженное в мм: .

9. Вычислить среднее приращение относительного удлинения за одну ступень нагружения и модуль Юнга .

Содержание отчета:

1. Эскиз образца с указанием размеров и схема установки тензометров.

2. Расчет предельной и допускаемой нагрузок.

3. Таблица экспериментальных данных.

4. Расчет модуля упругости Е.

Контрольные вопросы:

1. Что называют модулем упругости первого рода, и каков его физический смысл.

2. Из какого условия назначается максимальная растягивающая сила

3. Для чего применяют парное расположение тензометров.

4. Какова величина модуля Юнга для сталей.

5. Каков геометрический смысл модуля упругости первого рода при рассмотрении относительной диаграммы растяжения.

34