Все лабы по сопромату / ЛР9

Работа № 9

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ БАЛКИ

ПРИ ПРЯМОМ ИЗГИБЕ

Цель работы: экспериментально проверить теоретические формулы для определения перемещений балки при прямом изгибе.

Краткие теоретические сведения

Прямой изгиб осуществляется тогда, когда внешние силы действуют в плоскости, проходящей через одну из главных центральных осей поперечного сечения бруса. При этом плоскость изгиба (плоскость, в которой искривляется и перемещается ось бруса) совпадает с плоскостью действия внешних сил. Перемещение поперечных сечений бруса при изгибе характеризуют: прогибом и углом поворота .

Прогибом сечения называют перемещение центра тяжести сечения в направлении нормали к недеформированной оси балки.

Углом поворота сечения называют угол, на который плоскость сечения поворачивается относительно нейтральной линии.

Условие прочности при изгибе

,

1. где - максимальные нормальные напряжения при изгибе,

2. - максимальный изгибающий момент,

3. -момент сопротивления поперечного сечения,

4. -допускаемые напряжения при изгибе.

При упругом деформировании, когда справедлив закон Гука, напряжения не должны превышать предел пропорциональности , т.е. можно принять .

Кривизна изогнутой оси балки при изгибе , где - радиус изгиба балки, - жёсткость при изгибе.

Для определения прогиба сечения и угла поворота сечения можно воспользоваться методом непосредственного интегрирования:

дифференциальное уравнение изогнутой оси бруса

,

проинтегрировав которое получим уравнение углов поворота:

5. .

Проинтегрировав второй раз, получим уравнение прогибов:

6. ,

Константы интегрирования определяются из граничных условий.

При упругих деформациях перемещения и углы поворота можно определять методом начальных параметров из следующих универсальных уравнений:

7. 

8. ,

10. 

11. .

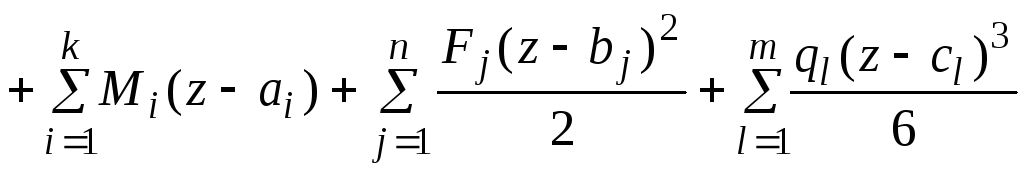Также для определения перемещений можно пользоваться интегралом Мора или способом Верещагина. При расчёте балок и рам, работающих на изгиб, в формуле Мора остаётся одно слагаемое:

12. ,

где – линейное или угловое перемещение,

- внутренние силовые факторы от действия единичной силы или единичного момента ,

- внутренние силовые факторы от действия заданных нагрузок.

Если брус состоит из участков с постоянной в пределах каждого участка жёсткостью, операцию интегрирования упрощают, пользуясь способом Верещагина (вместо аналитических выражений функций используются их эпюры):

13. ,

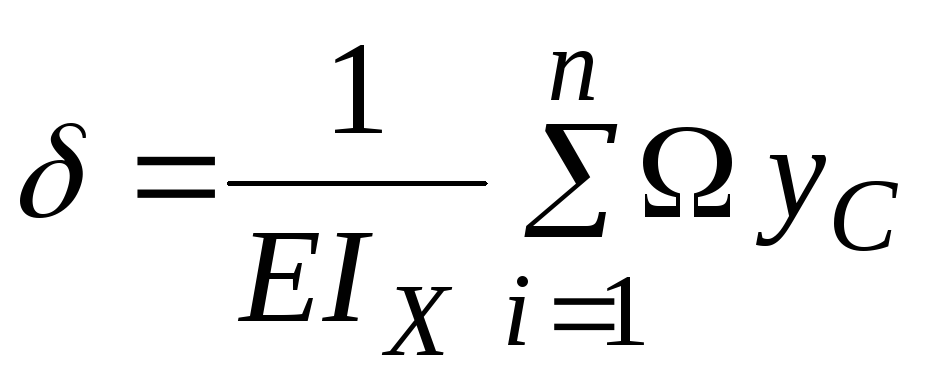14. где - линейное или угловое перемещение,

15. - площадь эпюры , т.е. грузовой от действия заданных нагрузок на участке ,

16. - высота эпюры соответствующая центру тяжести эпюры на участке , т.е. от действия единичной силы или единичного момента .

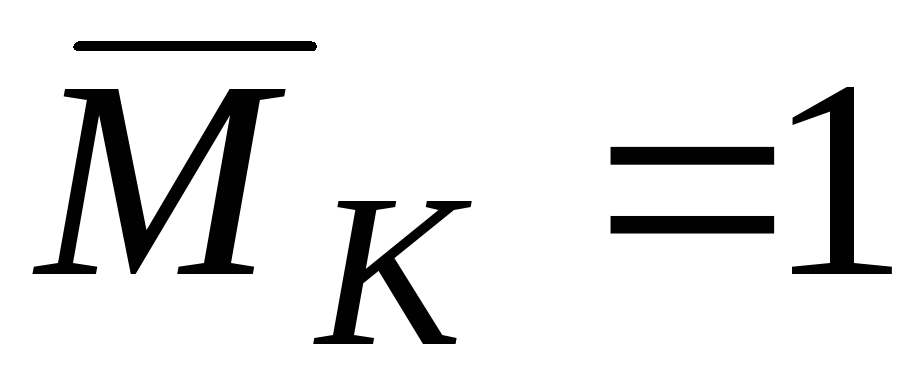Лабораторная установка

Установка для определения перемещений в балке (рис.28) состоит из основания с двумя призматическими опорами 1, на которые устанавливается стальная балка 2 прямоугольного поперечного сечения . Нагружение балки силой F производится с помощью передвигающейся по ней подвески 3 со сменными грузами.

Прогиб балки измеряют индикатором 4. Для измерения углов поворота к балке в ее опорных сечениях жестко прикреплены вертикальные стойки 5, с верхними концами которых на расстоянии Н от оси балки соприкасаются измерительные наконечники индикаторов 6. Угол поворота стойки равен углу поворота опорного сечения и определяется по формуле:

17. ,

где - перемещение измерительного наконечника индикатора 6.

Порядок выполнения работы:

1. Замерить линейкой расстояние между опорами l, высоту расположения индикаторов Н и штангенциркулем - размеры сечения балки b и h.

2. При заданном преподавателем значении размера a определить максимальную допустимую нагрузку, приняв для стали МПа:

, (20)

3. Определить экспериментально прогибы в сечениях с координатами 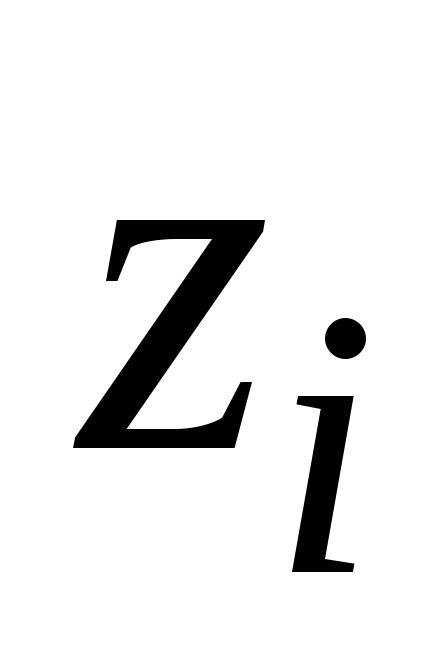, которые задаются преподавателем, и углы поворота опорных сечений.

4. Рассчитать способом Верещагина прогибы и углы поворота в этих же сечениях и сравнить теоретические и экспериментальные значения деформаций балки.

5. Результаты экспериментов и расчетов занести в таблицу.

Способ определения	,мм	… .				Углы поворота сечений, град
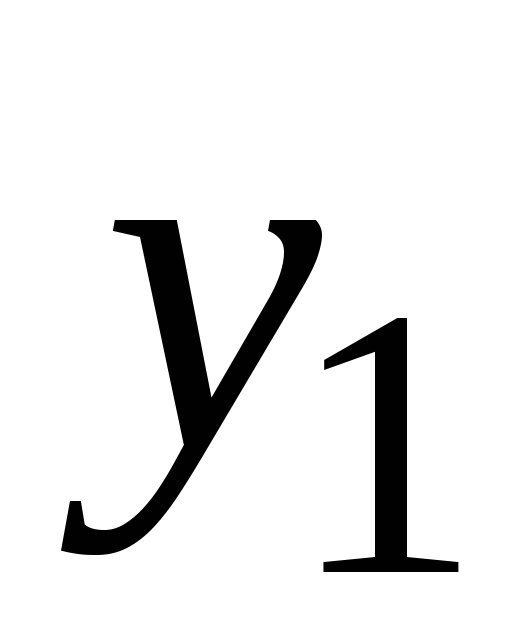	,мм	….
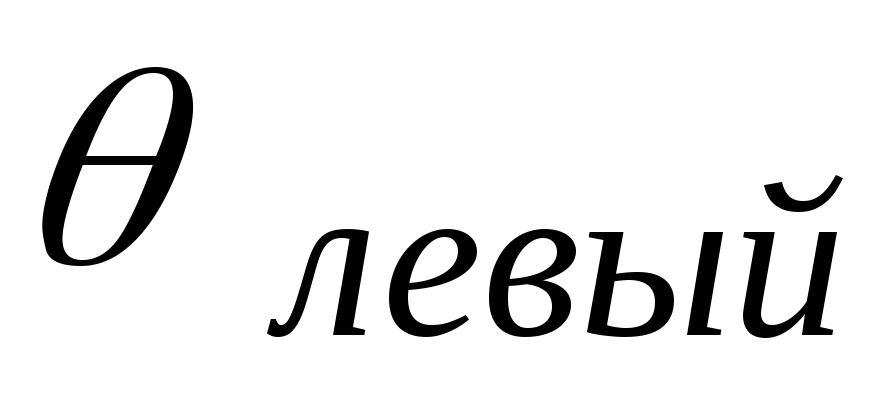
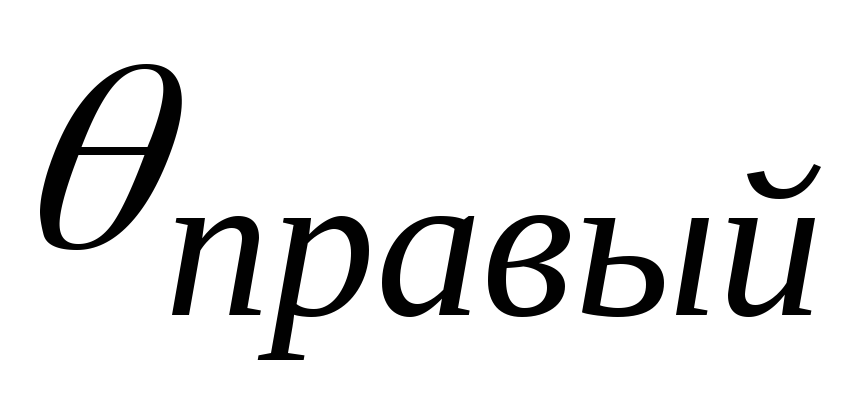
Расчет
Опыт

Содержание отчета:

1. Схема нагружения балки с необходимыми размерами.

2. Расчет перемещений по способу Верещагина.

3. Таблица экспериментальных и расчетных данных.

4. Выводы.

Контрольные вопросы:

1. Какой вид нагружения балки называется прямым изгибом?

2. Для чего определяется ? Вывести формулу (20).

3. У какой из двух балок при прочих равных условиях прогибы будут больше, у стальной или у алюминиевой? Почему?

4. Как рассчитать прогиб способом Верещагина?

5. Как рассчитать этим способом углы поворота опорных сечений?

63