Все лабы по сопромату / ЛР14

Работа № 14

ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ СИЛЫ ДЛЯ СЖАТОГО СТЕРЖНЯ

Цель работы

1. Ознакомиться с экспериментальным косвенным методом определения критической силы.

2. Экспериментально проверить формулу Эйлера для определения критической силы сжатого стержня большой гибкости.

Краткие теоретические сведения

При центральном сжатии прямого гибкого стержня его состояние равновесия может быть неустойчивым. Явление потери устойчивости сжатого стержня заключается в его переходе от прямолинейной формы равновесия к криволинейной. Наименьшая сила, при которой прямолинейная форма равновесия перестает быть устойчивой, называется критической силой.

Для стержней большой гибкости теоретическое значение критической силы рассчитывается по формуле Эйлера

, (33)

1. где Е – модуль упругости первого рода;

2. - минимальный момент инерции поперечного сечения;

3. - коэффициент приведения длины, зависящий от способа закрепления концов стержня;

4. l – длина стержня.

Формула Эйлера справедлива только при упругих деформациях, то есть когда критическое напряжение _кр (напряжение в момент потери устойчивости) не превосходит предела пропорциональности материала стержня _пц

,

5. где - гибкость стержня;

6. - наименьший радиус инерции поперечного сечения стержня.

Отсюда следует, что формулой Эйлера можно пользоваться, если гибкость стержня больше некоторой предельной гибкости, зависящей только от свойств материала

.

Непосредственно экспериментальное определение критической силы связано со значительными экспериментальными погрешностями, а значит и трудностями. Дело в том, что теоретически потеря устойчивости начинается при бесконечно малых прогибах стержня. Опытным путем фиксируются пусть и достаточно малые, но уже некоторые конечные изгибные деформации, т.е. деформации стержня уже после начала потери устойчивости. Значительная экспериментальная погрешность вызывается и начальной (пусть даже очень малой) кривизной оси бруса. Поэтому в данной работе для экспериментального определения критической силы используется так называемый косвенный метод. Метод основан на теоретическом решении задачи о продольном изгибе стержня (т.е. изгибе от действия продольной сжимающей силы), уже имеющего малую начальную кривизну. В выполняемой работе эта начальная кривизна вызвана уже наступившим явлением потери устойчивости. То есть в данном экспериментальном методе рассматривается дальнейшее развитие продольного изгиба стержня уже после потери его устойчивости.

Решение данной задачи может быть представлено в виде:

7. где f – конечное значение максимального прогиба в середине стержня от действия силы F;

8. f₀ - некоторое начальное значение прогиба в середине длины стержня;

9. F_кр – Эйлерова критическая сила для данного стержня.

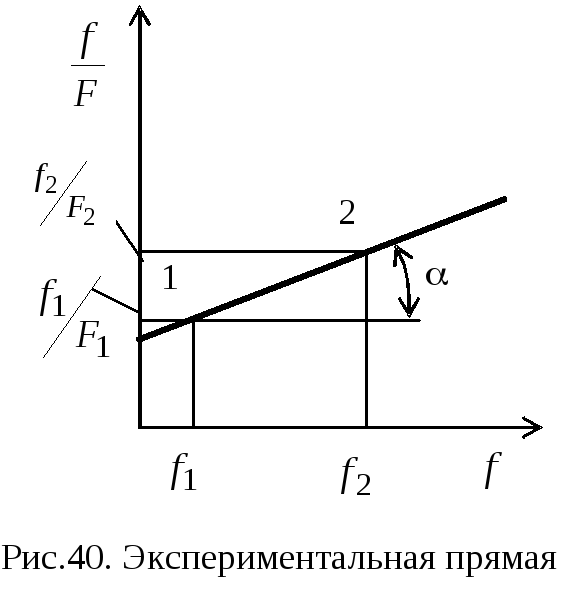
Это уравнение в координатах “ fF - f “ является уравнением прямой с угловым коэффициентом

.

Если построена экспериментальная прямая (рис.40) , то критическая сила находится как:

,

или через координаты двух экспериментальных точек 1 и 2 :

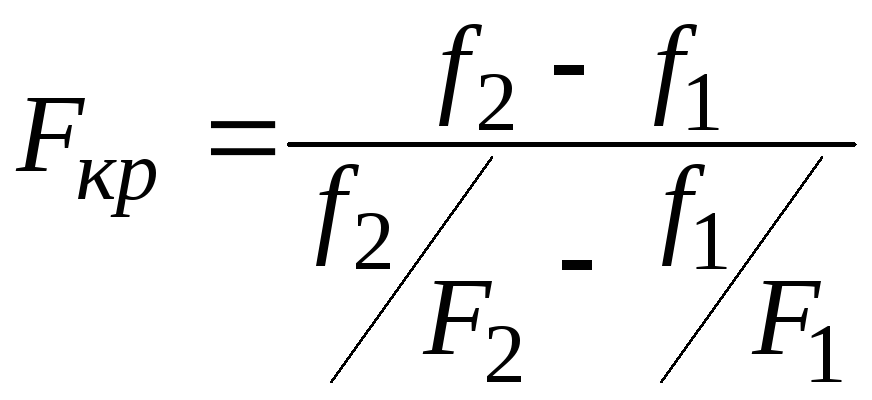. (34)

Таким образом, для экспериментального определения критической силы необходимо при двух последовательно приложенных продольных силах измерить два прогиба в середине стержня.

Лабораторная установка

Работа выполняется на установке, показанной на рис.41. Образец 1 представляет собой гибкий стержень прямоугольного сечения. Он устанавливается в два опорных гнезда верхнего 2 и нижнего 3 захватов. Винты 9 позволяют реализовывать три схемы закрепления концов стержня (рис.42).

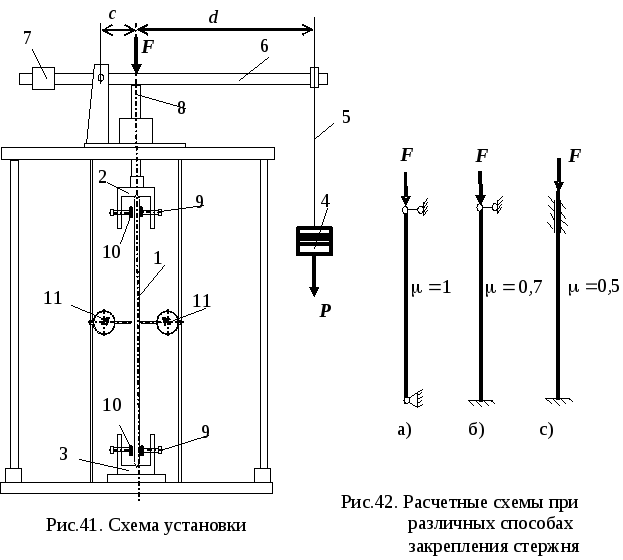
Если стержень не зажат винтами, то опирание следует считать шарнирным (рис.42,а). Закрепление одного конца соответствует схеме рис.42,б; закрепление двух концов – схеме рис.42,в. Закрепление осуществляется следующим образом. Между образцом 1 и винтами 9 устанавливают прокладки 10, после чего винты надежно затягивают симметрично с обеих сторон, чтобы избежать искривления стержня. Если конец образца закреплен, то его длина измеряется от края прокладки.

Нагрузка Р создается грузом 4 на подвесе 5. Она передается на образец через рычаг 6; поэтому сила, приложенная к образцу, равна:

.

Для того, чтобы исключить влияние веса рычага, на его свободном конце имеется противовес 7. Сила передается на стержень через толкатель 8 и верхний захват 2. Их вес нужно учесть и суммировать с силой F. Прогибы середины стержня измеряются индикаторами 11.

Порядок выполнения работы:

1. Закрепить концы стержня в соответствии с одной из схем рис.42. В дальнейшем эксперименты произвести по каждой из этих трех схем.

2. Измерить размеры образца: длину l; стороны поперечного сечения b и h и вычислить его геометрические характеристики:

.

Механические характеристики материала образца: МПа, = 390 МПа. Результаты измерений и расчетов занести в таблицу. Измерить плечи рычагов c и d.

l, мм	b, мм	h, мм	А, мм2	, мм	мм	

3. Сопоставить и . В случае применимости формулы Эйлера (33) рассчитать теоретическую величину критической силы.

4. С помощью грузов нагрузить образец продольной силой до его явного искривления за счет потери устойчивости. Определитьи измерить.

5. Нагрузить образец силой P2 и определить и .

6. По формуле (34) рассчитать экспериментальное значение критической силы. Данные экспериментов и расчетов занести в таблицу.

   № опыта		, Н	, Н	, мм	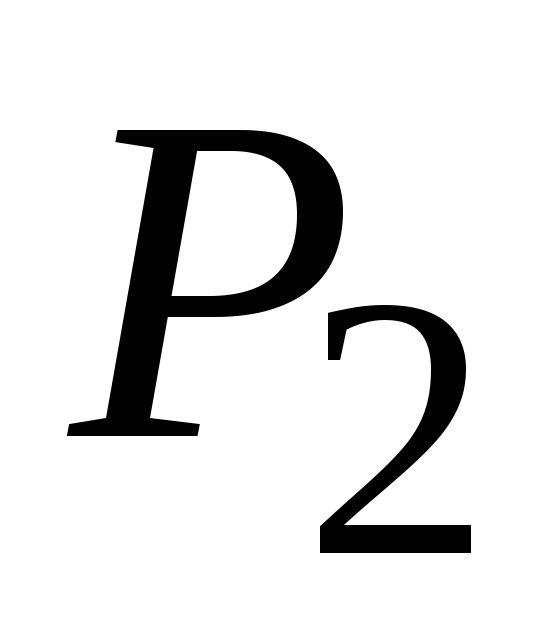, Н	, Н	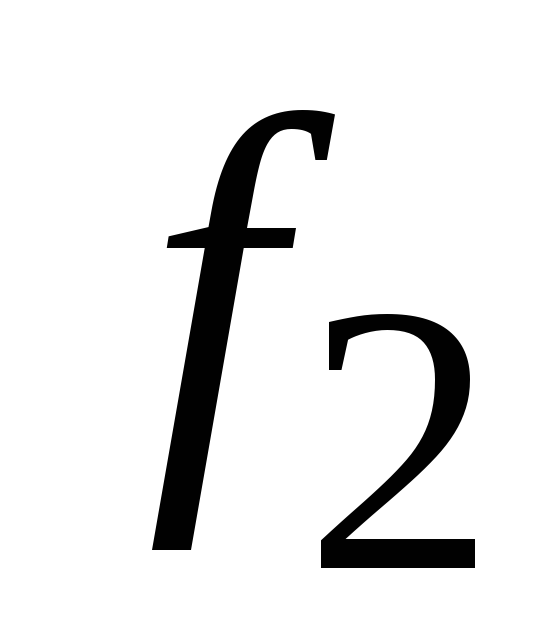, мм	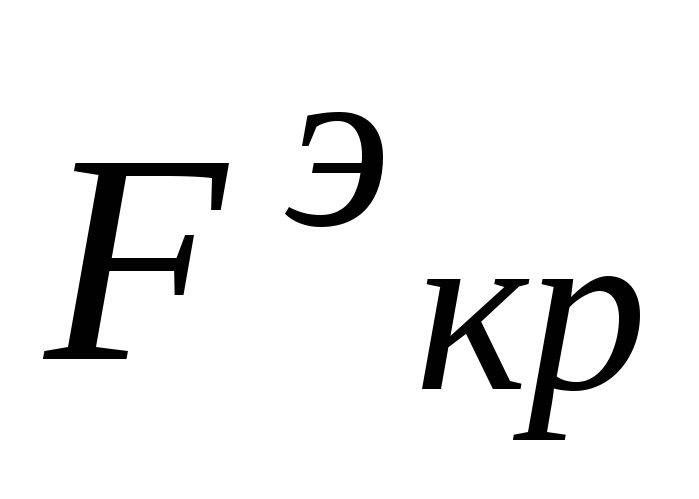, Н	, Н
   1
   2
   3

7. Сравнить экспериментальные и теоретические значения критических сил и сделать соответствующие выводы.

Содержание отчета:

1. Расчетные зависимости, по которым обрабатывались экспериментальные данные и велись теоретические расчеты.

2. Схемы закрепления и нагружения стержня.

3. Заполненные таблицы экспериментальных и расчетных данных.

4. График экспериментальной прямой (рис.40).

5. Выводы.

Контрольные вопросы:

1. Что является целью данной работы?

2. В чем заключается явление потери устойчивости сжатого стержня?

3. Что называется критической силой?

4. Как определяется теоретическое значение критической силы?

5. Каковы границы применимости формулы Эйлера и чем они обусловлены?

6. Что такое и чему равна гибкость стержня?

7. Что такое предельная гибкость стержня и как она определяется?

8. Как учитывается способ закрепление концов стержня при расчете критической силы?

9. Как экспериментально реализуются различные способы закрепления концов стержня?

10. В чем заключается косвенный метод экспериментального определения критической силы?

92