где А, В и С - заданные вещественные числа, причем из постоянных А и В хотя бы одна отлична от нуля, называется прямой на плоскости.

Постоянные А и В называются коэффициентами уравнения (1), С - свободным членом.

Уравнение (1) называется общим уравнением прямой.

Выясним геометрический смысл коэффициентов А и В. Для этого заметим, что уравнение (1) заведомо имеет хотя бы одно решение x0,y0, т.е. существует хотя бы одна точка M0(x0,y0), координаты которой удовлетворяют уравнению (1):

эквивалентное уравнению (1).

Уравнение (3) определяет прямую L, проходящую через точку M0(x0,y0) и перпендикулярно вектору n={A,B} (так как А и В одновременно не равны нулю, то вектор n ненулевой). Этот последний вектор мы будем называть нормальным вектором прямой (1).

Общее уравнение прямой (1) называется полным, если все его коэффициенты А, В и С отличны от нуля. Если хотя бы один из указанных коэффициентов равен нулю, уравнение называется неполным.

Рассмотрим все возможные виды неполных уравнений.

1)С = 0, уравнение Ax +By = 0 определяет прямую, проходящую через начало координат (поскольку координаты начала удовлетворяют этому уравнению).

2)В = 0, уравнение Ax + C = 0 определяет прямую, параллельную оси Oy (поскольку нормальный вектор этой прямой n={A,0} ортогонален оси Oy).

3)A = 0, уравнение By + C = 0 определяет прямую, параллельную оси Ox (поскольку нормальный вектор этой прямой n={0,B} ортогонален оси Ox).

4)В = 0 и С = 0, уравнение Ax = 0 определяет ось Oy (в самом деле, эта прямая параллельна оси Oy и проходит через начало координат).

5)А = 0 и С = 0, уравнение By = 0 определяет ось Ox (ибо эта прямая параллельна оси Ox и проходит через начало координат).

2.Другие формы уравнения прямой.

Рассмотрим теперь полное уравнение прямой (1) и покажем, что оно может быть приведено к следующему виду:

называемому уравнением прямой в отрезках.

Заметим, что в уравнении прямой в отрезках (6) числа a и b имеют простой геометрический смысл: они равны величинам отрезков, которые отсекает прямая на осях Ox и Oy соответственно (отрезки отсчитываются от начала координат, см. рис. 1), так как точки (a,0) и (0,b) удовлетворяют уравнению (6)

y

b

Рис. 1

Чтобы убедиться в этом, достаточно найти точки пересечения прямой, определяемой уравнением (6), с осями координат.

Уравнение прямой в отрезках удобно использовать для построения этой прямой на чертеже.

Каноническое уравнение прямой.

Любой ненулевой вектор, параллельный данной прямой, будем называть направляющим вектором этой прямой.

Поставим перед собой задачу: найти уравнение прямой, проходящей через данную точку M1(x1,y1) и имеющей заданный направляющий вектор q={l,m}.

Уравнение (7) и есть искомое уравнение прямой. Это уравнение называют обычно каноническим уравнением прямой.

Заметим, что в каноническом уравнении (7) один из знаменателей l или m может оказаться равным нулю (оба числа l и m равняться нулю не могут,

ибо вектор q={l,m} ненулевой). Так как всякую пропорцию ab = dc мы

договорились принимать как равенство ad=bc, обращение в нуль одного из знаменателей в (7) означает обращение в нуль и соответствующего числителя.

В заключении запишем уравнение прямой, проходящей через две данные точки M1(x1,y1) и M2(x2,y2) (конечно эти точки

считаются отличными друг от друга). Так как за направляющий вектор такой прямой можно взять вектор q= M1M2 ={x2 −x1, y2 − y1} и прямая проходит

через точку M1(x1,y1), то из канонического уравнения (6) получим уравнение искомой прямой в виде

Прямая с угловым коэффициентом.

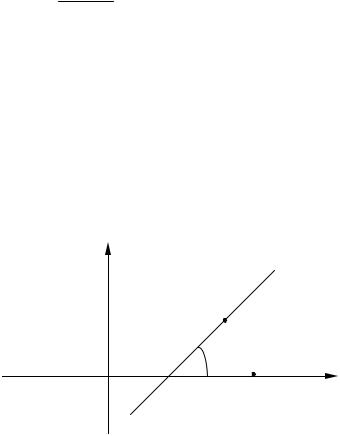
Рассмотрим любую прямую, не параллельную оси Ox. Введем понятие угла наклона прямой к оси Ox. Предположим, что рассматриваемая прямая пересекает ось Ox в точке А (рис. 2).

y

Рис. 2

Возьмем на оси Ox произвольную точку M, лежащую по ту сторону от точки A, куда направлена ось Ox, а на рассматриваемой прямой произвольную точку N, лежащую по ту сторону от точки A, куда направлена ось Oy. Угол α = NAM назовем углом наклона данной прямой к оси Ox.

Если прямая параллельна оси Ox или совпадает с ней, то угол наклона этой прямой к оси Ox мы будем считать равным нулю.

Тангенс угла наклона прямой к оси Ox назовем угловым коэффициентом этой прямой. Если обозначить буквой k угловой коэффициент данной прямой, а буквой α угол наклона этой прямой к оси Ox, то по определению можно записать k = tgα.

Заметим, что для прямой, параллельной оси Ox, угловой коэффициент равен нулю, а для прямой, перпендикулярной оси Ox, угловой коэффициент не существует (в последнем случае иногда формально говорят, что угловой коэффициент “обращается в бесконечность”).

Для того чтобы вывести уравнение прямой, проходящей через заданную точку M 1 ( x 1 , y 1 ) и имеющей данный угловой коэффициент k , умножим обе части канонического

уравнения (7) на m и учтем, что ml = k . Мы получим искомое уравнение в виде

Уравнение (11) называется уравнением прямой с угловым коэффициентом. В этом уравнении k обозначает угловой коэффициент данной прямой, а b представляет собой величину отрезка,

отсекаемого данной прямой на оси Oy, начиная от начала координат.

3. Взаимное расположение двух прямых.

а) Пусть сначала две прямые L1 и L2 заданы общими уравнениями

Aa1x + B1y + C1 = 0 и A2x + B2y + C2 = 0.

Так как нормальным вектором прямой L1 является вектор n1= {A1,B1}, а нормальным вектором прямой L2 является вектор n2= {A2, B2}, то задача об определении угла между прямыми L1 и L2 сводится к определению угла ϕ между векторами n1 и n2.

произведения получим

условию коллинеарности векторов n1 и n2, заключается в пропорциональности координат этих векторов, т.е. имеет вид

Условие перпендикулярности прямых L1 и L2 может быть извлечено из формулы (21) (при cosϕ = 0) или выражено равенством нулю

2) условие параллельности прямых L1 и L2:

3) условие перпендикулярности прямых L1 и L2:

(при этом числитель в (21′′) равен нулю, а знаменатель строго положителен). Условие перпендикулярности прямых L1 и L2 также можно получить из (21′′). Оно отвечает случаю, когда тангенс угла ϕ не существует, т.е. случаю

Прямая и плоскость в пространстве

где A, B, C, D - заданные вещественные числа, причем из постоянных A, B и C хотя бы одна отлична от нуля, называется плоскостью в

эквивалентное уравнению (1). Уравнение (3) (а стало быть и (1)) определяет плоскость π, проходящую через точку M0 (x0 , y0 ,z0 ) и перпендикулярную

вектору n ={A, B,C} (так как хотя бы одна из постоянных A, B, C не равна нулю, то вектор n ненулевой).

Этот последний вектор мы будем называть нормальным вектором плоскости (1).

2.Другие формы уравнений плоскости

Поставим перед собой цель - вывести уравнение плоскости, проходящей через три различные точки M1(x1,y1,z1), M2(x2,y2,z2) и M3(x3,y3,z3), не лежащие на одной прямой. Так как указанные три точки не лежат на одной прямой, векторы M1 M 2 = ( x2 − x1, y2 − y1, z2 − z1) и M 1 M 3 = ( x3 − x1, y3 − y1, z3 − z1) не коллинеарны, а поэтому точка M(x, y, z)

лежит в одной плоскости с точками M1, M2 и M3 тогда и только тогда, когда векторы M1 M2 , M1 M3 и M1M = (x − x1, y − y1, z − z1) компланарны,

т.е. тогда и только тогда, когда смешанное произведение этих трех векторов ровно нулю.

Используя выражение смешанного произведения в координатах, мы получим необходимое и достаточное условие принадлежности M(x, y, z) к указанной плоскости в виде

1. Способы задания прямой в пространстве.

Прямую линию в пространстве, являющуюся линией пересечения двух

При решении многих задач более удобным является специальный вид уравнений прямой в пространстве, к установлению которого и перейдем.

Договоримся называть любой ненулевой вектор, параллельный данной прямой, направляющим вектором этой прямой.

Выведем уравнения прямой, проходящей через данную точку пространства M1 (x1 , y1 ,z1 ) и имеющей заданный направляющий вектор

q ={l,m,n} . Для этого заметим, что точка M (x, y,z) лежит на указанной

Уравнение (4) суть искомые уравнения прямой, проходящей через точку M1 (x1 , y1 ,z1 ) и коллинеарной вектору q ={l,m,n} . Эти уравнения принято

называть каноническими уравнениями прямой.

Уравнения прямой, проходящей через две различные точки M1(x1,y1,z1) и M2(x2,y2,z2).

Тогда задача определения угла между этими прямыми сводится к определению угла ϕ между их направляющими векторами

q1 = {l1 ,m1 ,n1} и q2 = {l2 ,m2 ,n2}

Пользуясь определением скалярного произведения q1q2 = q1 q2 cosϕ и выражением в координатах указанного скалярного произведения и длин

извлечено из формулы (8) (при cosϕ = 0) или выражено равенством нулю

перпендикулярности векторов n и q и выражается равенством нулю

эквивалентно условию параллельности векторов n и q и выражается пропорциональностью координат этих векторов: