Var a, b : real;
begin
write ('введите a, b '); readln (a, b);
if a < b then b := b / 2;
writeln ( a:10:2, b:10:2 )
end.
В операторе ifнепосредственно за ключевыми словамиthenиelseмогут следовать любые операторы, в том числе и операторыif. В этом случае они называютсявложенными. Ниже приведены примеры, в которых используются вложенные операторыif.
Пример 3.11. Вычислить значение функции у по формуле при a > b.
Блок-схема алгоритма приведена на рис. 4.1. Здесь в линейную структуру вложена ветвящаяся, ветвь «нет» которой, в свою очередь, составляет еще одна ветвящаяся структура. Глубина вложения такой ветвящейся структуры равна 2.
Вложенная
ветвящаяся структура (глубина
вложения равна 1) Да
Да Нет
Нет
(глубина вложения
равна 2)Вложенная ветвящаяся структура
Рис.
3.1. Алгоритм с тремя ветвями
Программа имеет следующий вид.
var
X, y, a, b : real;
begin
writeln ('введите x, a, b ');
readln (x, a, b);
if x <= a then y := sqr (x)
else if x > b then y := sqr (sqr (x))
else y := x * sqr (x);
writeln ( y:10:2 )
end.
Пример 3.12. Составить программу решения следующей задачи
Схема алгоритма на рис 3.2.
Да
Нет
Да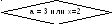
Нет
Рис.
3.2. Ветвление со сложными условиями
Программа имеет следующий вид:
Var X, a, z : real;
begin
write ('введите x,a'); readln (x, a);
if (a = 2) and (x = 1) then z := sqr (a * x)
else
if (a = 3) or (x = 2) then
z := exp (1 / 3 * ln (x*a))
else z := exp (1 / 5 * ln (x));
writeln ( z:10:2 )
end.
В отличие от предыдущих примеров, где в качестве условий в операторах if использовались выражения отношения, здесь условия представляют собой более сложные логические выражения, содержащие логические операции and и or. В большинстве случаев это делает программу более простой и понятной.
3.5. Оператор цикла с параметром
Циклическим называют вычислительный процесс, алгоритм которого представляет собой линейную структуру с вложенными в нее одной или несколькими циклическими структурами, каждая из которых имеет глубину вложения равную 1.
Для организации циклов используются специальные операторы языка, называемые операторами цикла. Познакомимся с оператором цикла с параметромFor.
Структура оператора
for переменная := начало to конец do оператор;
или
for переменная := начало downto конец do оператор;
где
- оператор - простой или составной оператор (тело цикла);
- переменная – параметр цикла;
- начало и конец – соответственно начальное и конечное значения параметра.
for ([фо] – для), to ([ту] – к), downto ([даунту] – уменьшать) – ключевые слова.
На параметр цикла в операторе for накладываются следующие ограничения:
1) в качестве параметра может использоваться только переменная порядкового типа (например, целого);
2) начальное и конечное значения параметра могут быть константами, переменными или выражениями, но должны иметь одинаковый с ним тип;
3) параметр цикла, а также его начальное и конечное значения не могут быть изменены никаким оператором в теле цикла;
4) после завершения цикла значение его параметра становится неопределенным.
Выполнение оператора с ключевым словом to. В этом варианте оператора необходимо, чтобы начало конец. В противном случае тело цикла не выполнится ни разу.
1. Вычисляются и запоминаются начальное и конечное значение параметра цикла (начало и конец).
2. Значение параметра (обозначим его i ) сравнивается с конечным значением конец. Если i конец, то выполняется тело цикла. В противном случае выполнение цикла прекращается.
3. Значение i увеличивается на 1 и повторяется шаг 2.
Выполнение оператора с ключевым словом downto. В этом варианте оператора необходимо, чтобы начало конец. В противном случае тело цикла не выполнится ни разу.
1. Вычисляются и запоминаются начальное и конечное значение параметра цикла (начало и конец).
2. Значение параметра (обозначим его j ) сравнивается с конечным значением конец. Если j конец, то выполняется тело цикла. В противном случае выполнение цикла прекращается.
3. Значение j уменьшается на 1 и повторяется шаг 2.
Пример 3.13. Вычислить значения функции y = sin (x 2) на отрезке [a, b], если шаг изменения её аргумента x.
В этой задаче количество повторений цикла равняется числу точек разбиения на отрезке [a, b] и может быть вычислено до выполнения цикла как целая часть от деления длины отрезка b – a на величину шага x плюс 1. Для вычисления целой части воспользуемся встроенной функцией trunc.