1.1. Основные сведения из теории

Диффузия представляет собой обусловленное тепловым движением перемещение атомов вещества в направлении убывания их концентрации.

Основой математического описания процессов диффузии являются два дифференциальных уравнения Фика. Первое уравнение (первый закон Фика) записывается следующим образом:

(3.1)

где J- плотность потока диффундирующего вещества, т.е. количество вещества, проходящего за единицу времени через единичную площадь поверхности, перпендикулярной направлению переноса вещества;

N - концентрация атомов примеси;

D - коэффициент диффузии.

Скорость переноса пропорциональна градиенту концентрации, а в качестве коэффициента пропорциональности вводится коэффициент диффузии. Знак минус в правой части (3.1) указывает на то, что диффузия происходит в направлении убывания концентрации. Другими словами, диффузия идет благодаря стремлению системы достичь физико-химического равновесия. Процесс будет продолжаться до тех пор, пока химические потенциалы компонентов всей системы не станут равными.

В макроскопическом представлении коэффициент диффузии определяет плотность потока вещества при единичном градиенте концентрации и является, таким образом, мерой скорости выравнивания градиента концентрации. Размерность коэффициента диффузии - м²/с (на практике чаще пользуются размерностью см²/с). В общем случае диффузия анизотропна и коэффициент диффузии зависит от кристаллографического направления.

Коэффициент диффузии при температуре диффузии определяют, используя известное выражение в форме уравнения Аррениуса

,

где предэкспоненциальный множитель D₀ (постоянная диффузии) - коэффициент диффузии при бесконечно большой температуре, см²/с;

ΔE - энергия активации диффузии, эВ;

k- постоянная Больцмана; T - температура процесса в градусах Кельвинах.

Диффузионные параметры различных элементов в кремнии, полученные различными исследователями, приведены в табл. 3.1

Таблица 3.1

Элемент	Множитель D0, см2/с	Энергия активации, эВ	Предельная растворимость при 12000С, см-3	Тип проводимости
Бор	5,1	3,7	1021	p
Алюминий	1,38	3,39	7.1018	p
Галлий	0,374	3,41	1020	p
Индий	0,785	3,63	1019	p
Фосфор	3,86	3,66	1022	n
Мышьяк	0,32	3,6	1020	n
Сурьма	5,6	3,98	1019	n
Висмут	100	4,6	1017	n
Железо	0,006	0,87	3.1016	-
Медь	0,04	0,43	1018	p
Золото	0,001	1,12	5.106	амфотерный
Литий	0,002	0,66	1019	n

Когда концентрация вещества изменяется только в одном направлении (одномерная диффузия) и при диффузии в изотропной среде (коэффициент диффузии - скаляр) первое уравнения Фика имеет следующий вид:

(3.2)

При простейшем анализе структур и в простейших моделях процессов легирования в технологии изготовления ИМС предполагаются именно такие условия диффузии.

Второе уравнение диффузии (второй закон Фика) получается путем сочетания первого закона и принципа сохранения вещества, согласно которому изменение концентрации вещества в данном объеме должно быть равно разности потоков этого вещества на входе в объем и выходе из него.

В общем случае второе уравнение диффузии имеет вид

(3.3)

Для одномерной диффузии в изотропной среде уравнение (3.3) можно записать

(3.4)

Второй закон Фика характеризует процесс изменения концентрации диффундирующей примеси во времени в различных точках среды и является математической моделью нестационарного (развивающегося) состояния системы (описывает период времени от начала процесса до установления стационарного состояния).

При постоянстве коэффициента диффузии D уравнение (3.4) упрощается

(3.5)

Допущение о постоянстве коэффициента диффузии справедливо в большинстве случаев, реализуемых в технологии ИМС.

Уравнения диффузии являются чисто феноменологическими, т.е. они не содержат никаких сведений о механизмах диффузии - о диффузионном процессе на атомном уровне. Кроме того, уравнения (3.1) - (3.5) не содержат информации о зарядовом состоянии диффундирующих частиц.

Процессы диффузии, используемые для изготовления интегральных структур, обычно анализируются с помощью частных решений уравнения (3.5) т.к., в отличие от (3.2), именно оно содержит важный параметр - время установления некоторого анализируемого состояния системы.

Основная цель решения уравнения - найти распределение примеси N(x,t) в полупроводнике после диффузии в течение определенного времени t при различных условиях осуществления процесса.

Общее решение уравнения (3.5) для бесконечного твердого тела при заданном в общем, виде начальном распределении примеси N(x,0) = f(x) может быть найдено методом разделения переменных. Оно имеет вид

, (3.6)

где ξ - текущая координата интегрирования.

Представленное выражение позволяет находить распределения примеси в твердом теле при любых начальных условиях. Решение конкретной задачи сводится к подстановке в (3.6) соответствующих ситуации начальных условий с последующими, как правило, очень громоздкими преобразованиями. Практически при создании полупроводниковых ИМС представляют интерес три частных случая: диффузии из полубесконечного пространства, диффузия из постоянного источника и диффузии из бесконечно тонкого слоя.

Диффузия из полубесконечного пространства (диффузия из концентрационного порога).

Диффундирующая примесь (диффузиант) поступает в полубесконечное тело через плоскость x = 0 из второго полубесконечного тела (источника) с равномерным распределением примеси. Концентрация примеси в источнике – N₀. Предполагается, что в принимающем диффузант теле нет рассматриваемой примеси.

Начальное распределение концентраций для этого случая задается в виде

для x < 0,

для x > 0.

Решением уравнения (3.6) для этого случая является выражение

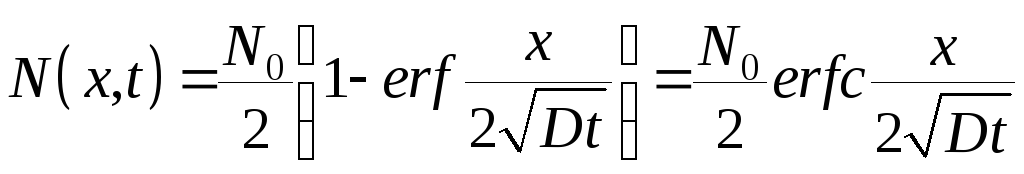, (3.7)

где erf z - называют интегралом ошибок Гаусса или функцией ошибок (error function) Гаусса аргумента z. В соответствии с сокращением это распределение называют erf – распределением:

. (3.8)

В математике часто используют как самостоятельную и другую функцию

, (3.9)

которая называется дополнением функции ошибок до единицы или дополнительной функцией ошибок - error function complement. Обе функции табулированы.

 Величинаимеет размерность длины и носит название диффузионной длины или длины диффузии. Физический смысл этого параметра - среднее расстояние, которое преодолели диффундирующие частицы в направлении выравнивания градиента концентрации за время t.

Рассмотренное решение можно использовать как простейшую модель, представляющую распределение примеси на границе эпитаксиальная пленка – подложка.

Диффузия из постоянного источника.

Диффузант поступает в полубесконечное тело через плоскость x = 0 из источника, обеспечивающего постоянную концентрацию примеси N₀ на поверхности раздела твердое тело - источник в течение любого времени. Такой источник называют бесконечным или источником бесконечной мощности. Полагается, что в принимающем диффузиант теле нет рассматриваемой примеси.

Начальное распределение концентраций и граничные условия для этого случая задаются в виде

для x = 0,

для x >0.

Решением уравнения (3.6) для данных условий является выражение

(3.10)

Если в объеме полупроводникового материала до диффузии имелась примесь противоположного типа по отношению к диффундирующей, эта примесь распределена по объему равномерно и её концентрация равна N_исх, то в этом случае в полупроводнике образуется электронно-дырочный переход. Его положение (глубина залегания) x_p-n определяется условием N(x,t) = N_исх , откуда

(3.11)

и (3.12),

где здесь запись erfc^-1 обозначает аргумент z функции erfc.

Рассмотренная модель диффузионного процесса с постоянным источником описывает процесс диффузионного легирования полупроводникового материала из газовой или паровой фазы. Этот процесс используется при создании сильно легированных диффузионных слоев (например, эмиттерных) с поверхностными концентрациями N₀ близкими к значениям предельной твердой растворимости примеси N_пред в данном полупроводниковом материале.

Твердое тело можно считать полубесконечным в том случае, если его размеры в направлении движения диффузианта много больше длины диффузии.

Диффузии из бесконечно тонкого слоя в полубесконечное тело с отражающей границей на поверхности. Примером диффузии примеси из тонкого слоя в полубесконечное тело с отражающей границей является диффузия в кремниевую пластину из эпитаксиального, имплантированного или диффузионного слоя и покрытую слоем двуокиси кремния SiO₂ или нитрида кремния Si₃N₄. Границу пластины и пленки можно с большой долей правдоподобия принять отражающей, т.к. коэффициенты диффузии большинства примесей в кремний на несколько порядков больше, чем в двуокись кремния и нитрид кремния.

Решение диффузионного уравнения при этих условиях находится в виде

(3.13)

Приведенное выражение представляет собой Гауссово распределение.

При решении этой задачи необходимо знать количество примеси Q, накопленной в твердом теле при диффузии в течение времени t. Эта величина определяется по формуле

(3.14)

где J(0,t) - поток диффузанта в объем через плоскость x = 0.

Следует обратить внимание на возрастающее со временем значение накопленной в диффузионном слое примеси при диффузии с данными граничными условиями.Диффузию из бесконечно тонкого слоя в сочетании с диффузией из постоянного источника в полуограниченное тело нашли широкое практическое применение при формировании диффузионных p-n-переходов методом двухступенчатой диффузии.

На первой стадии процесса проводится кратковременная диффузия (при пониженных температурах) из постоянного источника, распределение примеси после которой описывается выражением (3.10). Значение N_o при этом велико и определяется либо пределом растворимости данной примеси в полупроводниковом материале, либо концентрацией примеси в стеклообразном слое на поверхности полупроводника. Этот этап часто называют "загонкой".

После окончания первой стадии пластины помещают в другую печь для последующей диффузии, обычно, при более высоких температурах. В этой печи нет источника примеси, а если он создавался на первой стадии в виде стеклообразного слоя на поверхности пластин, его предварительно удаляют. Таким образом, тонкий слой легированного полупроводника, полученный на первом этапе, является источником перераспределяемой примеси при проведении второй стадии процесса. Для создания отражающей границы второй этап (часто называемый "разгонкой") проводят в окислительной атмосфере. При этом на поверхности растет слой SiO₂.

Существует заметное несоответствие между распределением примеси в источнике, сформированном при загонке, с декларируемым при выводе выражения (3.14) - ступенчатым. Это несоответствие должно отразиться на точности описания реального распределения примеси после второй стадии диффузии выражением (3.14).

При моделировании двухстадийной диффузии и анализе результатов процесса полагают, что выражение (3.14) достаточно точно соответствует реальному при условии, если величина произведения D₁t₁ для первого этапа процесса легирования значительно меньше, чем D₂t₂ для второго – D₂t₂ >> D₁t₁. Это условие быстрой истощаемости источника. В этом случае, учитывая, что количество накопленной при первом этапе примеси определяется соотношением

из (3.14) получим

(3.15)

Величины D₂ и t₂ относятся ко второй стадии диффузии.

Тонкий слой на поверхности полупроводниковой пластины является источником, который очень быстро истощается. Непрерывная диффузия в этом случае приводит к постоянному понижению поверхностной концентрации примеси в полупроводнике. Эту особенность данного процесса используют в полупроводниковой технологии для получения контролируемых значений низкой поверхностной концентрации примеси, например, для создания базовых областей кремниевых транзисторных структур дискретных приборов или ИМС.