Статистика для курсовика / 4. Статист. Метод указ Методы анализа / 2.5.1. Ан.структ

78

Анализ структурных различий в пространстве

При анализе структурных различий в пространстве (территориальных сравнений структур) используется система показателей, включающая индивидуальные и обобщающие показатели.

К индивидуальным показателям относятся:

 «абсолютный» показатель (слово «абсолютный» взято в кавычки, так как при расчете разности удельных весов этот показатель является абсолютным только по методике расчета, размерность этого показателя  %)

 относительный показатель

где  удельный вес i-й структурной группы территории А и В (объекта А и В).

При сравнении двух структур используются следующие обобщающие показатели:

 линейный и квадратический коэффициенты структурных различий Л. Казинца;

 интегральный коэффициент структурных различий К. Гатева;

 индекс структурных различий А. Салаи;

 коэффициент ранговой корреляции Спирмена.

При сравнении одновременно нескольких структур применяется коэффициент неравномерности распределения.

Линейный и квадратический коэффициенты структурных различий Л. Казинца двух структур рассчитываются следующим образом:

 при сравнении в пространстве двух структур А и В

где  удельный вес структурной группы территории А и В;  число структурных частей (групп).

Интегральный коэффициент структурных различий К. Гатева рассчитывается по формуле

Индекс структурных различий А. Салаи определяется следующим образом

Если интегральный коэффициент структурных различий К. Гатева или индекс структурных различий А. Салаи близки к нулю, то это характеризует отсутствие структурных сдвигов. Если коэффициенты равны 0,4-0,5, то наблюдаются значительные изменения структуры.

Коэффициент ранговой корреляции Спирмена характеризует изменение приоритетов в структурах и определяется по формуле

где  ранги группы в структуре территории А и В.

Чем ближе коэффициент Спирмена к нулю, тем существеннее различия в структурах. Значения коэффициента характеризуют изменения приоритетов в распределении групп.

Сравнение нескольких структур осуществляется с помощью коэффициента неравномерности распределения признака, который рассчитывается для каждой структуры по формуле

где  число доминантных групп.

Доминантными называются группы, в которых сосредоточено от 60 до 80% единиц совокупности, остальные группы – малозначимыми. Наиболее распространенный тип явления называется приоритетным.

Если коэффициент неравномерности распределения равен нулю, то признак равномерно распределен в статистической совокупности или по элементам признака, т. е. удельный вес всех групп совокупности или элементов признака одинаковый. Неравномерность распределения признака возрастает с увеличением коэффициента неравномерности распределения.

Анализ структурных сдвигов во времени

Абсолютные значения численностей совокупности и признаков могут быть моментными (на определенную дату) и интервальными (за период времени), поэтому и структуры совокупностей и признаков также могут быть моментными (например, структура населения по возрасту на начало года, структура основных фондов на начало года) и интервальными (например, структура затрат на производство продукции за год, структура среднегодовой численности персонала предприятия).

При анализе структурных сдвигов во времени (анализ динамики структуры) используется система показателей, включающая индивидуальные и обобщающие показатели. Индивидуальные показатели характеризуют изменение во времени удельного веса одной группы статистической совокупности или элемента признака. Обобщающие – показывают структурные сдвиги во времени по всем группам или элементам.

К индивидуальным показателям структурных сдвигов, характеризующим изменение i-й структурной части за два периода или момента времени относятся «абсолютный» прирост и темп роста удельного веса.

«Абсолютный» прирост удельного веса характеризует изменение удельного веса i-й структурной части в j-й период или момент времени по сравнению с (j1)-м периодом или моментом времени

Сумма «абсолютных» приростов для всех k структурных групп в j-й период или момент времени всегда равна нулю

Темп роста удельного веса i-й структурной части в j-й период или момент времени рассчитывается по формуле

где  удельный вес i-й структурной части в j-й и (j1)-й период или момент времени.

Индивидуальными показателям структурных сдвигов, характеризующими изменение i-й структурной части за несколько (больше двух) периодов или моментов времени, являются средний «абсолютный» прирост удельного веса, средний темп роста удельного веса.

Средний «абсолютный» прирост удельного веса i-й структурной части за n периодов или моментов времени

где  удельный вес i-й структурной части в последний (n-й) и первый период или момент времени.

Сумма средних «абсолютных» приростов для всех k структурных частей всегда равна нулю

Средний темп роста удельного веса i-й структурной части за n периодов или моментов времени

Обобщающими показателями, характеризующими структурные сдвиги структур за два периода или момента времени используются:

 линейный коэффициент «абсолютных» структурных сдвигов;

 квадратический коэффициент «абсолютных» структурных сдвигов;

 квадратический коэффициент относительных структурных сдвигов;

 интегральный коэффициент структурных сдвигов К. Гатева;

 индекс структурных различий А. Салаи;

 коэффициент ранговой корреляции Спирмена.

При сравнении структур за несколько периодов или моментов времени применяются

 линейный коэффициент «абсолютных» структурных сдвигов за n периодов или моментов времени;

 коэффициент неравномерности распределения.

Линейный коэффициент «абсолютных» структурных сдвигов при сравнении во времени двух структур (например, структур домохозяйств одного района в отчетном и базисном периодах) рассчитывается следующим образом:

где  удельный вес группы в отчетный и базисный период или момент времени;  число структурных частей (групп).

Линейный коэффициент «абсолютных» структурных сдвигов характеризует среднее изменение удельного веса по всем структурным группам за рассматриваемый интервал времени.

Квадратический коэффициент «абсолютных» структурных сдвигов определяется по формуле

Квадратический коэффициент относительных структурных сдвигов

показывает средний относительный прирост удельного веса по всем структурным группам за рассматриваемый интервал времени.

Интегральный коэффициент структурных различий К. Гатева рассчитывается по формуле

Индекс структурных различий А. Салаи определяется следующим образом

Коэффициент ранговой корреляции Спирмена определяется по формуле

где  ранги группы в отчетном и базисном периоде или момент времени.

Линейный коэффициент «абсолютных» структурных сдвигов за n периодов или моментов времени используется для анализа структурных сдвигов в целом по всем структурным группам и за несколько периодов времени. Коэффициент рассчитывается по формуле

Сравнение нескольких структур осуществляется с помощью коэффициента неравномерности распределения, который рассчитывается для структуры в каждом периоде или моменте времени. Коэффициент неравномерности в в j-й период или момент времени рассчитывается следующим образом

где  общее количество групп и число доминантных групп в j-й период или момент времени;  доля i-й структурной части в j-й период или момент времени.

Изменение структуры может быть с сохранением приоритетов и со сменой приоритетов. Смена приоритетов происходит либо внутри доминантных групп, что соответствует незначительным изменениям структуры, либо малозначимые группы становятся приоритетными, что соответствует значительным изменениям структуры. Значительные изменения структуры, как правило, происходят в течение длительных промежутков времени.

При анализе динамики структуры статистической совокупности или признака за два отрезка времени, состоящих из n периодов или моментов времени, рассчитывается средний удельный вес на каждом отрезке времени, а затем осуществляется сравнение средних структур.

Средний удельный вес i-й структурной части за n периодов или моментов времени рассчитывается следующим образом

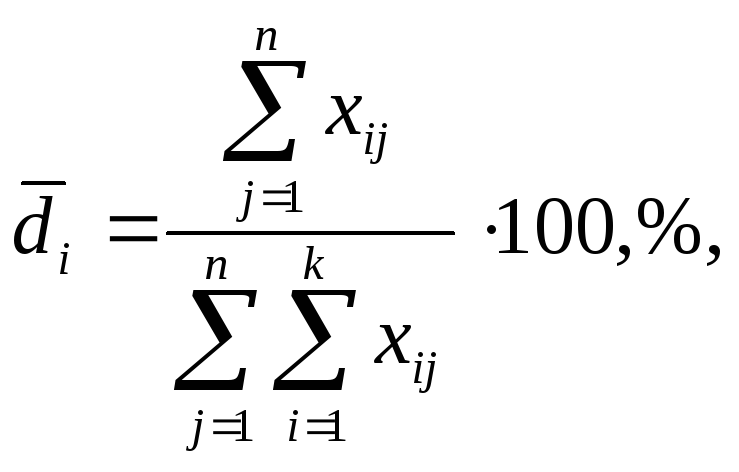
где  абсолютный размер i-й структурной части в j-й период или момент времени; n  число периодов или моментов времени;  число структурных частей.

Исключение влияния структурных изменений на величину показателя

На величину средних показателей в статистической совокупности оказывает влияние изменение структуры объекта. Для определения влияния изменения структуры на изучаемый показатель x используется индекс структурных сдвигов, который рассчитывается

 при анализе во времени

где  доля группы статистической совокупности в базисном и отчетном периодах;

 величина изучаемого показателя в базисном периоде;

 при анализе в пространстве

где  доля группы статистической совокупности на территории А и В;

 величина изучаемого показателя в статистической совокупности на территории В.

Исключить влияние структурных сдвигов можно путем использования стандартизованной структуры при расчете средних показателей.

Средний показатель в статистической совокупности, рассчитанный с использованием стандартизованной структуры, называется стандартизованный показатель и определяется следующим образом

где  средняя величина или доля изучаемого признака в i-й группе статистической совокупности;

 число единиц совокупности i-й группы в стандартизованной структуре;

 доля единиц совокупности i-й группы в стандартизованной структуре, которая рассчитывается следующим образом

В качестве стандарта при анализе динамики могут быть приняты данные по той же территории за предыдущие годы, по стране в целом и т. д., при территориальных сравнениях – средняя структура по двум территориям, по стране в целом.

Средний удельный вес i-й структурной части по всем объектам (территориям) рассчитывается по формуле

где  абсолютный размер i-й структурной части j-го объекта; J  число объектов (территорий).