71

5. АНАЛИЗ СТРУКТУРЫ СТАТИСТИЧЕСКИХ

СОВОКУПНОСТЕЙ И ПРИЗНАКОВ

2. Методические указания к решению задач

по теме «Анализ структуры статистических совокупностей

и признаков»

Структура (от лат. structura – строение, расположение, порядок) – это состав и внутренние связи объекта.

Структура статистической совокупности – это распределение единиц, образующих статистическую совокупность, по группам в соответствии со значениями того или иного признака.

Структура признака – это совокупность элементов признака, выделенных по какому-либо количественному или качественному показателю.

Изучение структуры и структурных изменений статистических совокупностей и признаков включает в себя

 расчет показателей доли и удельного веса;

 анализ дифференциации и концентрации признака в статистической совокупности;

 анализ структурных различий в пространстве;

 анализ структурных сдвигов (изменения структуры) во времени;

 анализ влияния структуры на изменение признака.

Показатели доли и удельного веса

Структура статистической совокупности и признака характеризуются абсолютным и относительным показателями.

Абсолютный показатель структуры совокупности – частота или количество единиц совокупности в i-й структурной части (группе).

Относительными показателями структуры статистической совокупности являются доля (частость) и удельный вес структурной части совокупности, которые рассчитываются по следующим формулам:

 доля i-й структурной части

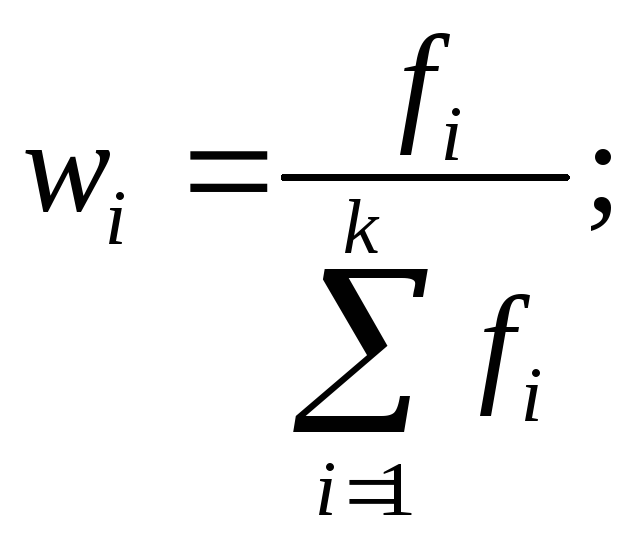
 удельный вес i-й структурной части

где  численность (частота) i-й структурной группы статистической совокупности;

k  число структурных частей (групп) совокупности.

Абсолютный показатель структуры признака – абсолютное значения показателя i-й структурной части (элемента) признака.

Относительные показатели структуры признака

 доля i-й структурной части признака

 удельный вес i-й структурной части признака

где  абсолютное значения показателя i-й структурной части признака;

k  число структурных частей (элементов) признака.

Сумма удельных весов всех k структурных частей составляет

Анализ дифференциации признака в статистической совокупности

Показатели дифференциации характеризуют распределение признака по единицам статистической совокупности и рассчитываются в том случае, когда признаки расположены в виде вариационного ряда (в порядке возрастания).

К основным показателям дифференциации, изучающим структуру вариационного ряда признака, относятся:

 медиана;

 квантили (квартили, квинтили, децили и процентили);

 децильный коэффициент дифференциации;

 коэффициент фондов.

Медиана является структурным средним показателем. Медианой называется варианта, которая находится в середине вариационного ряда по частоте. Медиана делит ряд пополам, по обе стороны от нее находится одинаковое количество единиц совокупности. Медиана показывает количественную границу варьирующего признака, которую достигла половина единиц совокупности.

В интервальном ряду распределения медиана рассчитывается следующим образом

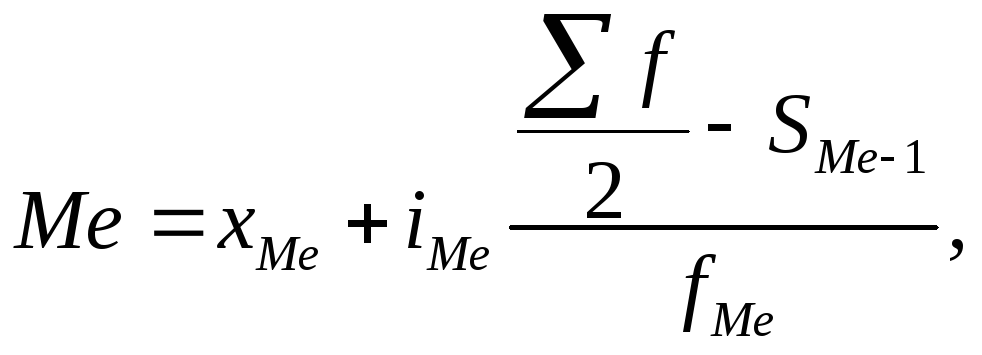
где  нижняя граница медианного интервала;

 величина медианного интервала;

 частота (или доля, или удельный вес), накопленная до медианного интервала;

 частота (или доля, или удельный вес) медианного интервала.

При анализе структуры рядов распределения кроме структурных средних величин используются квиртили, квартили, децили и процентили, формулы расчета которых аналогичны формуле расчета медианы.

Дополнительно к медиане для характеристики структуры вариационного ряда вычисляются квантили: квартили, квинтили, децили и процентили.

Квартили делят ряд распределения признака по частоте на 4 равные части; квинтили делят ряд на 5 равных частей; децили  на 10 частей; процентили  на 100 частей. Второй квартиль, пятый дециль и пятидесятый процентиль равны медиане. Формулы расчета квантилей аналогичны формуле медианы.

Квартили.

Первый и третий квартили вычисляются аналогично расчету медианы, только вместо медианного интервала берется для первого квартиля интервал, в котором находится варианта, отсекающая 1/4 численности частот, а для третьего квантиля  варианта, отсекающая 3/4 численности частот.

где  нижняя граница интервала, в котором находится k-й квартиль;

 величина интервала, в котором находится k-й квартиль;

 частота (или доля, или удельный вес), накопленная до интервала, в котором находится k-й квартиль;

 частота (или доля, или удельный вес) интервала, в котором находится k-й квартиль.

Квинтили рассчитываются по формуле

где  нижняя граница интервала, в котором находится k-й квинтиль;

 величина интервала, в котором находится k-й квинтиль;

 частота (или доля, или удельный вес), накопленная до интервала, в котором находится k-й квинтиль;

 частота (или доля, или удельный вес) интервала, в котором находится k-й квинтиль.

Децили определяются следующим образом

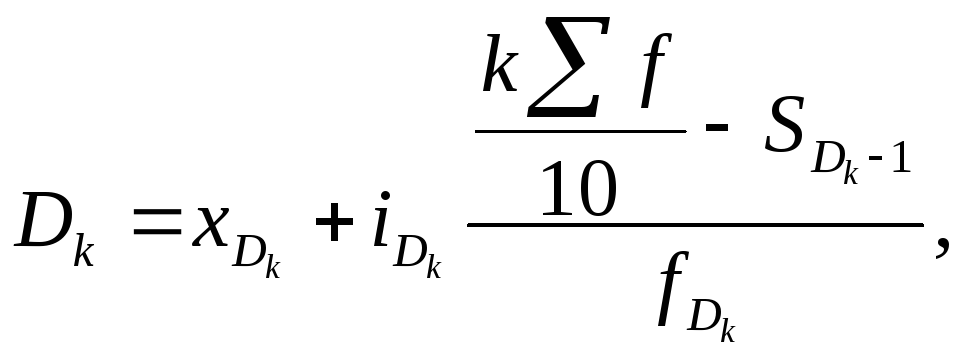
где  нижняя граница интервала, в котором находится k-й дециль;

 величина интервала, в котором находится k-й дециль;

 частота (или доля, или удельный вес), накопленная до интервала, в котором находится k-й дециль;

 частота (или доля, или удельный вес) интервала, в котором находится k-й дециль.

Процентили рассчитываются по формуле

где  нижняя граница интервала, в котором находится k-й процентиль;

 величина интервала, в котором находится k-й процентиль;

 частота (или доля, или удельный вес), накопленная до интервала, в котором находится k-й процентиль;

 частота (или доля, или удельный вес) интервала, в котором находится k-й процентиль.

Децильный коэффициент дифференциации признака определяется следующим образом

где  первый и девятый децили.

Децильный коэффициент дифференциации характеризует соотношение минимального значения признака 10% численности статистической совокупности с самыми высокими значениями признака и максимального значения признака 10% численности совокупности с наименьшими значениями признака.

Первый и девятый децили рассчитываются по формулам

где  нижняя граница первого и девятого децильного интервала;

 величина первого и девятого децильного интервала;

 частота (или доля, или удельный вес), накопленная до первого и девятого децильного интервала;

 частота (или доля, или удельный вес) первого и девятого децильного интервала.

Коэффициент фондов показывает соотношение средних значений признака в десятой и первой децильных группах

где  среднее значение признака в первом и десятом децильных интервалах, т. е. среднее значение признака 10% численности статистической совокупности с наименьшими значениями признака и 10%  с наибольшими значениями признака.

Среднее значение признака в первом децильном интервале (середина первого децильного интервала)

где  нижняя граница первого децильного интервала;

 величина первого дециля или верхняя граница первого децильного интервала.

Среднее значение признака в десятом децильном интервале (середина десятого децильного интервала)

где  нижняя граница десятого децильного интервала или величина девятого дециля;

 величина десятого дециля или верхняя граница десятого децильного интервала.

Расчет среднего значения признака в первом и десятом децилях выполняется для одинаковой численности совокупности (10%), поэтому коэффициент фондов может быть рассчитан по формуле

где  суммарное значение признака в первом и десятом децильных интервалах.

Анализ концентрации признака в статистической совокупности

К основным показателям, характеризующим концентрацию признака в статистической совокупности, относятся: коэффициенты концентрации признака Лоренца и Джини.

Коэффициент концентрации признака Лоренца определяется по формуле

где  доля суммарного значения признака в i -й группы статистической совокупности;

 доля численности единиц совокупности в i -й группе;

n  число интервалов группировки.

Коэффициент концентрации доходов Джини рассчитывается по формуле

где  кумулятивная (накопленная) доля признака.

Коэффициенты концентрации Лоренца и Джини лежат в пределах от 0 до единицы. Чем ближе к 1 значения коэффициентов, тем выше уровень концентрации признака, т.е. больше неравномерность распределения признака по единицам совокупности. При нуле получается равномерное распределение признака.

Коэффициенты концентрации Лоренца и Джини применяются в основном в социальной статистике, например, для оценки концентрации доходов населения. Для наглядного представления концентрации доходов населения строится кривая Лоренца (рис. 5.1) в прямоугольной системе координат: по оси абсцисс откладываются накопленные доли численности населения (), а по оси ординат  накопленные доли денежных доходов населения (). В случае равномерного распределения доходов по группам населения кривая Лоренца совпадает с прямой  линией равномерного распределения. Если имеется отклонение от равномерного распределения, кривая Лоренца находится ниже линии равномерного распределения. Коэффициент Лоренца соответствует площади а, расположенной между линией равномерного распределения и кривой Лоренца (см. рис. 5.1).

Рис. 5.1. Кривая концентрации доходов Лоренца

Коэффициент Джини можно рассчитать по графику концентрации доходов населения (рис. 5.1) как соотношение площадей