37

2. СРЕДНИЕ ПОКАЗАТЕЛИ

1. Методические указания к решению задач

по теме «Средние показатели»

Средняя величина является обобщенной количественной характеристикой признака в статистической совокупности. Вычисление средней величины должно осуществляться с учетом экономического содержания изучаемого показателя.

Средние величины делятся на два класса: степенные средние (средняя арифметическая, гармоническая, геометрическая, квадратическая и др.); структурные средние (мода, медиана). На рис. 2.1 приведена структура средних показателей.

Средние показатели

Степенные

средние

Структурные

средние

арифметическая

мода

гармоническая

медиана

геометрическая

квадратическая

Рис. 2.1. Структура средних показателей

Степенные средние величины

Средняя арифметическая рассчитывается следующим образом:

 средняя арифметическая простая (невзвешенная)

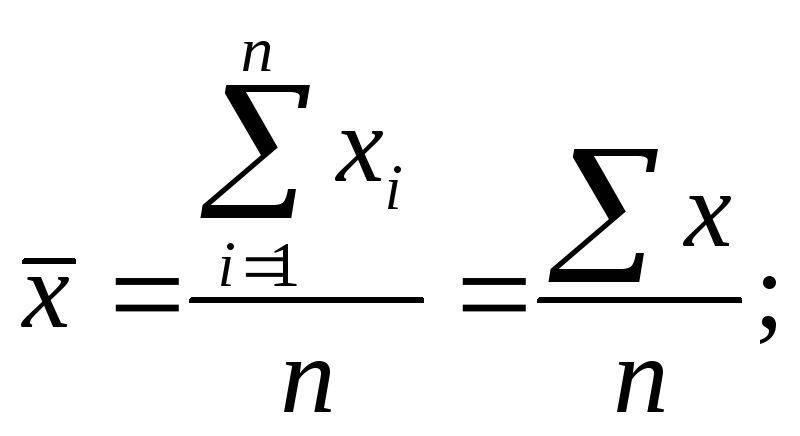
 средняя арифметическая взвешенная

где x  значения (варианты) признака;

n  число вариантов (число наблюдений), из которых рассчитывается средняя;

f  статистический вес (число повторений значения признака).

Если известны произведения , то среднюю величину можно вычислить по формуле средней агрегатной

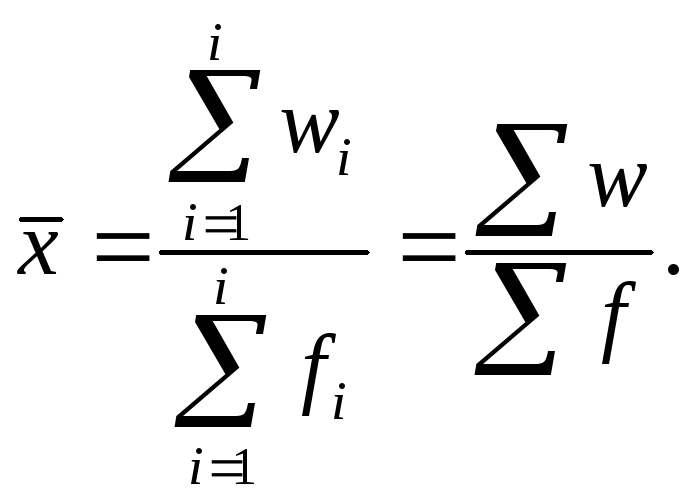
Средняя гармоническая вычисляется из обратных значений признака:

 средняя гармоническая простая (невзвешенная)

 средняя гармоническая взвешенная

где

Средняя геометрическая невзвешенная рассчитывается по формулам:

 средняя геометрическая простая (невзвешенная)

 средняя геометрическая взвешенная

Средняя геометрическая применяется, например, при вычислении средних темпов роста (см. п. 4 «Показатели рядов динамики»).

Средняя квадратическая рассчитывается по формулам:

 средняя квадратическая простая (невзвешенная)

 средняя квадратическая взвешенная

Формула средней квадратической применяется для расчета среднего квадратического отклонения (см. п. 3 «Показатели вариации»).

Выбор формулы расчета средней величины зависит от задачи исследования, содержания изучаемого явления и исходной информации.

При определении средних величин в интервальном вариационном ряду в случае открытых крайних интервалов необходимо определить нижнюю границу первого и верхнюю границу последнего интервалов. Для этого используются величины других, закрытых интервалов: величина интервала первой группы условно принимается равной величине интервала последующей, а величина интервала последней группы  величине интервала предыдущей. В интервальном ряду распределений необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается середина интервала.

Основные свойства средней арифметической величины

1. Произведение средней величины и суммы частот равно сумме произведений значений (вариант) признака на частоты

2. Если из каждой варианты вычесть какое-либо произвольное число, то новая средняя уменьшается на то же число

Тогда средняя величина исходных значений

3. Если к каждой варианте прибавить какое-либо произвольное число, то новая средняя увеличится на то же число

Тогда средняя величина исходных значений

4. Если каждую варианту разделить на какое-либо произвольное число, то средняя арифметическая уменьшится во столько же раз

Тогда средняя величина исходных значений

5. Если каждую варианту умножить на какое-либо произвольное число, то средняя арифметическая увеличится во столько же раз

Тогда средняя величина исходных значений

6. Если все частоты умножить (разделить) на какое-либо число, то средняя не изменяется

7. Если все варианты имеют одинаковую частоту (f₁ = f₂ = …= f_n = k), то средняя арифметическая взвешенная равна средней арифметической простой

8. Сумма отклонений, как от простой, так и от взвешенной средней арифметической равна нулю

Использование свойств 2 и 4 позволяет значительно упростить расчеты и вычислить арифметическую среднюю в сгруппированном ряду распределения по формуле

где m₁  момент первого порядка

Метод упрощенного расчета средней величины называется методом отсчета от условного нуля или способом моментов.

Степенные средние используются для расчета хронологических, многомерных и других средних показателей.

Средняя хронологическая является характеристикой ряда динамики и рассчитывается для интервальных и моментных рядов с равноотстоящими и неравноотстоящими уровнями (см. п. 4 «Показатели рядов динамики»).

Средняя многомерная величина рассчитывается для каждой i-й единицы статистической совокупности по формуле

где k  количество признаков, характеризующих единицу статистической совокупности;  нормированное значение j-го признака i-й единицы совокупности, определяется следующим образом

где  значение j-го признака i-й единицы статистической совокупности;  среднее значение j-го признака в статистической совокупности.

Структурные средние показатели

Средние показатели являются обобщающими характеристиками варь-ирующего признака. Вспомогательными описательными характеристиками вариационного ряда являются структурные средние показатели: мода и медиана.

Модой называется величина признака (вариант), которая чаще всего встречается в статистической совокупности. В вариационном ряду это будет значение показателя, имеющее наибольшую частоту.

Для интервального ряда распределения мода рассчитывается по следующей формуле

где  нижняя граница модального интервала;  величина модального интервала;  частота модального, предшествующего модальному и последующего за модальным интервала.

Медианой называется варианта, которая находится в середине вариационного ряда по частоте. Медиана делит ряд пополам, по обе стороны от нее находится одинаковое количество единиц совокупности. Медиана показывает количественную границу варьирующего признака, которую достигла половина членов совокупности.

В интервальном ряду распределения медиана рассчитывается следующим образом

где  нижняя граница медианного интервала;  величина медианного интервала;  частота, накопленная до медианного интервала;  частота медианного интервала.

При анализе структуры рядов распределения кроме структурных средних величин используются квиртили, квартили, децили и процентили, формулы расчета которых аналогичны формуле расчета медианы.