Примеры решения задач по теме «Средние показатели» Средняя арифметическая величина
Задача 2.1
Имеются данные о средней заработной плате и числе рабочих различной квалификации (табл. 2.1).
Таблица 2.1
Заработная плата и число рабочих
|
Квалификация рабочего |
Разряд рабочего |
Средняя заработная плата, ЗПi , тыс. р./мес. |
Число рабочих, Ni , чел. |
|
1. Низкая |
1; 2
|
6,0 6,5 6,8 |
1 1 1 |
|
2. Средняя |
3; 4 |
8,2 8,8 9,0 |
2 2 2 |
|
3. Высокая |
5; 6 |
10,5 12,0 12,6 |
3 5 2 |
|
Итого |
|
19 |
Определить среднюю заработную плату рабочих каждой квалификации и всех рабочих.
Решение
1. Средняя заработная плата j-й квалификации рабочих (групповая средняя величина) рассчитывается следующим образом
где ФЗПj фонд заработной платы рабочих j-й квалификации; Nj число рабочих j-й квалификации.
2. Средняя заработная плата рабочих низкой (первой) квалификации может быть рассчитана по формуле простой средней, т. к. значения заработной платы этой категории рабочих не повторяются
3. Для рабочих средней квалификации средняя заработная плата рассчитывается по формуле средней взвешенной
или
по формуле простой средней, т. к.
статистический вес (число рабочих)
одинаковый для различных значений
заработной платы
4. Средняя заработная платы рабочих высокой квалификации
5. Средняя заработная плата всех рабочих (общая средняя величина) по формуле
средней арифметической взвешенной с использованием всех значений заработной платы
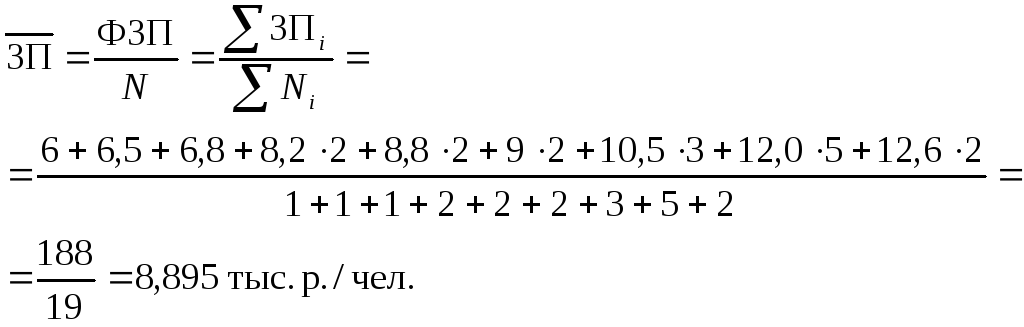
средней арифметической взвешенной с использованием средних значений заработной платы рабочих по каждой квалификационной группе
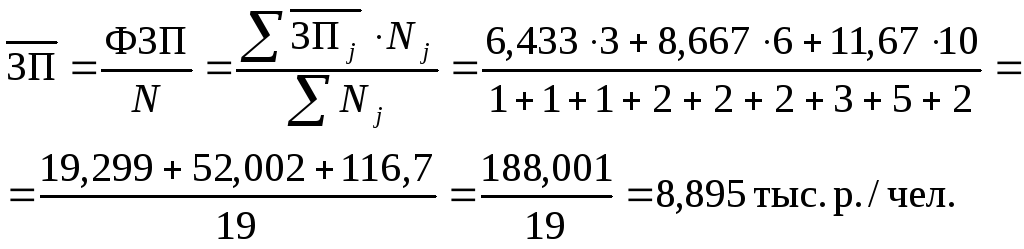
средней агрегатной с использованием величины фонда заработной платы и численности рабочих по каждой квалификационной группе
Задача 2.2
Имеются данные о возрасте работников предприятия в виде интервального ряда распределения работников по возрасту (графы 1, 2 или 1, 3 табл. 2.2).
Таблица 2.2
Распределение рабочих по возрасту
|
Номер группы работников |
Возраст рабочих, лет |
Число рабочих, Ni, чел. |
Удельный вес рабочих, di,, % |
Средний возраст рабочих в группе, Вi, лет |
|
|
|
А |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
20 25 |
200 |
10 |
22,5 |
4500 |
225,0 |
|
2 |
25 30 |
900 |
45 |
27,5 |
24750 |
1237,5 |
|
3 |
30 35 |
800 |
40 |
32,5 |
26000 |
1300,0 |
|
4 |
35 40 |
100 |
5 |
37,5 |
3750 |
187,5 |
|
Итого |
|
2000 |
100 |
|
59000 |
2950,0 |
Определить средний возраст работника предприятия.
Решение
Для расчета среднего возраста работника в интервальном ряду распределения необходимо определить середину интервала (графа 4 табл. 1.25). Средний возраст работника может быть рассчитан с использованием в качестве статистических весов
численности работников (графа 5 табл. 2.2)
удельного веса работников каждой группы в общей численности работников (графа 6 табл. 2.2)
Задача 2.3
Имеются данные о численности высоко- и низкоквалифицированных рабочих и средней месячной заработной плате по двум предприятиям (табл. 2.3).
Таблица 2.3