Организация учета фактического состояния
Фактическое состояние вводится для каждого объекта и каждого периода в тех единицах, в которых установлен объем всех работ, введенный в ячейку К10. Так, для первого периода фактическое выполнение работ для объекта А вводится в D5; для объекта Б — в D7; для объекта В — в D9. Суммарное фактическое состояние вычисляется по формуле, введенной в D11.
Определение показателей, характеризующих состояние работ
В качестве таких показателей принимаем две величины. Их значения введены в С13:С14, из которых видно, что:
к1 показывает отклонение факта от плана в абсолютных значениях;
к2 показывает отклонение факта от плана в процентах.
Формулы для вычисления этих показателей введены в ячейки D13:K14.
Для наглядного представления состояния работ удобно строить гистограммы. Например, построим диаграмму, характеризующую состояние работ по всему объекту за второй период.
Алгоритм 8.2.2. Графическое представление результатов
В таблице (рис. 8.2.2) скопировать C14, F14, G14 в C12, F12, G12 и выделить С3, С10:С12, F3:G3, F10:G12.
Мастер диаграмм:
шаг 2 — Гистограмма.
шаг 3 — Вид 2.
шаг 4 — переключатель В строках,
ввести: 1 стр., 1 столб.
шаг 5 — ввести название диаграммы.
Форматировать диаграмму по алг. 2.2.4:
убрать фон;
ввести метки значений.
На экране: рис. 8.2.4.
Рис. 8.2.4.
Аналогично по алгоритмам, приведенным в главе 2, построена диаграмма на рис. 8.2.5.
Рис. 8.2.5
Такие диаграммы, которые показывают результат распределения финансирования и фактическое состояние работ, весьма полезны как для оценки текущего состояния, так и для принятия решений.
8.2.2. Эвристическое распределение финансирования в иерархической структуре
Эвристическое распределение финансирования в иерархической структуре производится по следующему алгоритму
Алгоритм 8.2.3. Эвристическое распределение финансирования в иерархической структуре
Определить число уровней и структуру каждого уровня.
Задачу будем решать для иерархической структуры, характеристики которой приведены на рис. 8.2.6.
Рис. 8.2.6
На втором уровне принимаем, что объект А состоит из двух объектов А1 и А2. Для А1 и А2 будем распределять ресурсы, выделяемые во втором квартале, по месяцам апрель-июнь. На третьем уровне будем распределять на 4 недели ресурсы, выделяемые для объекта А1 в мае.
Сводную таблицу рис. 8.2.1 и рис. 8.2.2 скопировать для каждого уровня.
На рис. 8.2.7. приводятся формулы, на рис. 8.2.8. — данные.
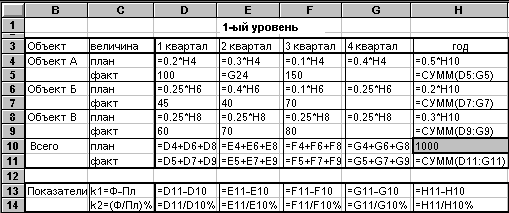
Рис. 8.2.7
Рис. 8.2.7 (продолжение)
Рис. 8.2.8
Модифицировать таблицы для 2-го и 3-го уровней в соответствии с рис. 8.2.6 с помощью удаления строк и столбцов.
Установить правила и ввести формулы для распределения ресурсов на 2-ом уровне (рис. 8.2.7):
Связь между уровнями обеспечивается вводом в ячейку G23 адреса Е4.
Ввести формулы для распределения величины, находящейся в ячейке G23, между объектами А1 и А2 в ячейки G19, G21.
Ввести формулы распределения этих величин по месяцам для А1 в ячейки D19:F19, для А2 — в D21:F21.
Аналогично ввести зависимости для 3-го уровня: в ячейку H32 = E19 и в ячейки D32:G32 — правила распределения суммарных ресурсов для объекта А1 в мае месяце по неделям.
Ввести формулы, учитывающие фактическое состояние:
Данные для 3-го уровня вводятся в ячейки D33:G33.
Переход от 3-го уровня ко 2-му производится по формуле, введенной в Е20 = Н33.
Переход от 2-го уровня к 1-му производится по формулам, введенным в Е5 = G24.
Ввести исходное значение распределяемых ресурсов для первого уровня в ячейку Н10.
Ввести фактическое состояние для третьего уровня в ячейки D33:G33.
Ввести остальные фактические значения, не входящие в третий уровень: D20, F20, D22:F22 и т. д.