Задачи оптимального проектирования
9.1. Постановка задачи оптимального проектирования
9.1.1. Основные понятия и определения
Каждый объект проектирования (ОП) обладает определенными свойствами. Эти свойства могут быть как количественными, так и качественными. Примерами количественных свойств могут быть масса, производительность, стоимость и т. д. Примерами качественных свойств — надежность, удобство эксплуатации, и, наконец, само понятие "качество".
Как правило, качественные свойства ОП непосредственно оценить числом не удается, поэтому, если надо учитывать качественные свойства, их следует выразить количественными величинами, которые можно измерить. Так, качественное понятие "надежность" можно измерить вероятностью безотказной работы, временем наработки на отказ и т. д.
В дальнейшем будем учитывать только те свойства ОП, которые могут быть измерены. Такие количественные характеристики будем называть параметрами. С точки зрения содержания параметры могут быть техническими и экономическими. Примеры технических параметров — производительность, мощность; примеры экономических параметров — стоимость изделия, трудоемкость изготовления.
Параметры делятся на заданные и искомые. Правила перехода от заданных параметров к искомым называются расчетом. Если в расчет входят только технические параметры, его называют инженерным расчетом. В том случае, когда в расчет наряду с техническими параметрами входят и экономические, расчет является технико-экономическим.
По методу проведения расчеты могут быть проверочными и проектировочными. Для иллюстрации методов расчета вернемся к задаче о баке, которую мы уже рассматривали в главе 1. Объем бака
V = abh,
где a, b — стороны основания бака, h — высота бака.
При проверочном расчете задаются некоторыми значениями всех параметров а, b, h и проверяют, равняется ли их произведение заданному значению объема V.
При проектировочном расчете устанавливают зависимость искомых параметров от заданных, которая для бака имеет вид:
.
При заданном значении V, выбирая различные a и b, определяют значение h. Расчет, в котором принимается несколько вариантов значений а и b, называется многовариантным.
Рассмотрим, что дает многовариантный расчет.
Рис.
9.1.2
Рис.
9.1.1
|
Вариант |
a |
b |
h |
|
1 |
10 |
5 |
40 |
|
2 |
10 |
20 |
10 |
|
3 |
10 |
35 |
5,7 |
Полезность многовариантного проектирования очевидна. Действительно, трудно себе представить, что первый же принятый вариант окажется наилучшим. Однако при проведении многовариантного расчета всегда возникает достаточно сложный вопрос: какой вариант выбрать?
В рассматриваемом случае сравнение различных вариантов будем производить по двум величинам:
S — полной поверхности бака, которая определяет количество необходимого материала;
L — длине сварного шва, показанного на рис. 9.1.3 штриховой линией, которая определяет потребную рабочую силу.
Полная поверхность и длина сварного шва определяются так:
|
Вариант |
S |
L |
|
1 |
1300 |
80 |
|
2 |
1000 |
110 |
|
3 |
1213 |
166 |
Значения этих величин для трех рассмотренных вариантов представлены на рис. 9.1.4.
Рис.
9.1.3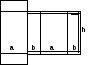
Рис. 9.1.4
Вариант может быть лучшим только в одном единственном смысле, определяемом назначенным критерием. Сравнивая эти результаты, можно сделать следующие выводы:
Наилучшим вариантом в смысле минимального расхода материала является вариант 2, для него S = 1000.
Наилучшим вариантом в смысле минимальной длины сварного шва является вариант 1, для него L = 80.
И еще одно важное замечание. Говоря о наилучшем варианте, мы имели в виду наилучший из тех вариантов, для которых был выполнен расчет, т. е. наилучший из рассмотренных вариантов. Но очевидно, что наилучший из рассмотренных совершенно не обязательно будет наилучшим из всех возможных. Даже более того. Трудно себе представить, что в число рассматриваемых вариантов, полученных традиционными методами вариантного проектирования, войдет вариант, наилучший из всех возможных. Такой вариант, наилучший в принятом смысле из всех возможных, может быть получен только в результате оптимального проектирования.