
- •Предисловие
- •Введение
- •Пример 1.
- •Пример 2.
- •Глава 1. Анализ данных
- •§1. Состав исходной информации
- •§2. Интерполяционный полином Лагранжа
- •Случай 1.
- •Случай 2.
- •Случай 3.
- •Случай n.
- •§3. Парная линейная регрессия. Метод наименьших квадратов
- •§4. Множественная линейная регрессия
- •§5. Нелинейные модели
- •§6. Системы одновременных эконометрических уравнений
- •Глава 2. Временные ряды §7. Составляющие временного ряда
- •§8. Определение составляющих временного ряда
- •При этом коэффициенты ak, bk будут равны
- •§9. Временной ряд как случайный процесс
- •§10. Модели arima
- •§11. Учет сезонных составляющих
- •Глава 3. Оценка качества спецификации модели §12. Анализ погрешностей исходной информации
- •§13. Доверительные интервалы
- •§14. Расчет погрешностей
- •§15. Коэффициент детерминации
- •§16. Средняя ошибка аппроксимации
- •§17. Принцип максимального правдоподобия. Построение регрессионных моделей при гетероскедастичности ошибок
- •§18. Статистические гипотезы
- •Список литературы
- •Оглавление
§15. Коэффициент детерминации
Коэффициент
детерминации
 характеризует качество регрессионной
модели.
характеризует качество регрессионной
модели.
Значения различных величин, полученных расчетами, будем в дальнейшем обозначать «».
Рассмотрим
случай парной регрессии
 .
Имеет место равенство
.
Имеет место равенство .
Для суммы квадратов отклоненийyi
от среднего
.
Для суммы квадратов отклоненийyi
от среднего
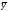
 (TSS
–
total sum of squares)
(TSS
–
total sum of squares)
имеем
TSS
= RSS+ESS,
где
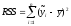 сумма
квадратов
отклонений,
объясненная
регрессией
(RSS
— regression
sum of squares),
сумма
квадратов
отклонений,
объясненная
регрессией
(RSS
— regression
sum of squares),
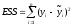 остаточная
сумма
квадратов
отклонений
(ESS
– error
sum of squares).
остаточная
сумма
квадратов
отклонений
(ESS
– error
sum of squares).
Коэффициент детерминации определяется по формуле:
.
 . (15.1)
. (15.1)
Из (15.1) видно, что R2[0,1] и чем меньше R2 отличается от 1, тем лучше регрессионная модель.
В
математической статистике вводится
выборочный коэффициент корреляции
 между данными наблюдений(xi,yi),
i=1,
2,
…, n.
Напомним, что
между данными наблюдений(xi,yi),
i=1,
2,
…, n.
Напомним, что
 ,
, ,
,
 .
.
Поскольку
 ,
величинуr
можно
представить в виде
,
величинуr
можно
представить в виде
 .
С другой стороны
.
С другой стороны ,
, ,
откуда следует, что
,
откуда следует, что
 .
.
Поэтому
 ,
т.е. коэффициент детерминации равен
квадрату выборочного коэффициента
корреляции .
,
т.е. коэффициент детерминации равен
квадрату выборочного коэффициента
корреляции .
§16. Средняя ошибка аппроксимации
Фактические значения интересующей нас величины отличаются от рассчитанных по уравнению регрессии. Чем меньше это отличие, чем ближе рассчитанные значения подходят к эмпирическим данным, тем лучше качество модели. Величина отклонений фактических и расчетных значений переменной величины по каждому наблюдению представляет собой ошибку аппроксимации. Так как отклонение может быть величиной как положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
Отклонения
( )
рассматриваются как абсолютная ошибка
аппроксимации, тогда
)
рассматриваются как абсолютная ошибка
аппроксимации, тогда – относительная ошибка аппроксимации.
– относительная ошибка аппроксимации.
Средняя
ошибка аппроксимации определяется как
среднее арифметическое:
 .
Иногда пользуются определением средней
ошибки аппроксимации, имеющим вид
.
Иногда пользуются определением средней
ошибки аппроксимации, имеющим вид .
.
§17. Принцип максимального правдоподобия. Построение регрессионных моделей при гетероскедастичности ошибок
Для нахождения неизвестных величин по результатам измерений, содержащих случайные погрешности, служит метод наименьших квадратов (МНК). Определяемые величины обычно связаны уравнениями, образующими избыточную систему.
Метод наименьших квадратов строит оценки на основе минимизации суммы квадратов остатков. Для его применения необходимо выполнение следующих пяти условий:
случайный характер остатков;
нулевая средняя величина остатков, не зависящих от независимой переменной;
гомоскедастичность – дисперсия каждого отклонения i одинакова для всех значений переменной;
отсутствие автокорреляции остатков. Значения i распределены независимо друг от друга;
остатки подчиняются нормальному распределению.
Для возможности применения МНК необходимо проверить характер остатков i по всем пяти условиям.
Если величины i являются случайными величинами, распределенными по нормальному закону - i(0,2), так что Ei = 0, Di=2 и некоррелированы - cov (i, j) = 0 (i j), а значит, и независимы, то можно применить МНК. Постоянство 2
для
всех i
означает равноточность задания величины
yi;
величины xi
мы считаем заданными точно. Свойство
равноточности измерения yi
иначе называется гомоскедастичностью.
Если же
 иi
различны, то говорят о гетероскедастичности
регрессионной
модели.
иi
различны, то говорят о гетероскедастичности
регрессионной
модели.
Пусть
эмпирические данные наблюдений (x1,
x2,
…, xn)
характеризуют случайную величину
xN(,
2),
для которой математическое ожидание
=
Ex
и дисперсия
2
= Dx
неизвестны и их требуется оценить.
Выпишем функции плотности нормального
распределения
 .
Согласнопринципу
максимального
правдоподобия
предполагаем,
что функция L=f(x1)f(x2)…f(xn)
принимает наибольшее значение при
истинных значениях параметров и 2.
Удобнее иметь дело с
.
Согласнопринципу
максимального
правдоподобия
предполагаем,
что функция L=f(x1)f(x2)…f(xn)
принимает наибольшее значение при
истинных значениях параметров и 2.
Удобнее иметь дело с
 .
.
В
нашем примере
 ,
поэтому
,
поэтому
 .
.
Выпишем необходимые условия экстремума функции ln L (и L):
 ,
,
 .
.
Решение этой системы уравнений после простых преобразований приводит к оценкам
 ,
,
 .
.
Заметим, что
 ,
,
 .
.
Пример показывает, что принцип максимального правдоподобия не обязательно приводит к несмещенной оценке искомых параметров.
Воспользуемся
принципом максимального правдоподобия
для анализа гетероскедастичности. В
этом случае модель парной линейной
регрессии имеет вид yi
=
a+bxi+i
, где Ei
=
0,
Di
=
i2,
так что i(0,
i2).
Соответствующие плотности вероятностей
 .
Логарифмическая функция правдоподобия
.
Логарифмическая функция правдоподобия
 .
.
Теперь ясно, как модифицировать МНК в случае гетероскедастичности ошибки i :
 .
.
В случае гомоскедастичности дисперсии i равны и мы получаем классическую формулировку МНК.
Часто
вводится веса наблюдений
 ,
при этом число выбирается так, чтобы
веса были целыми числами. МНК сводится
к минимизации взвешенных сумм квадратов:
,
при этом число выбирается так, чтобы
веса были целыми числами. МНК сводится
к минимизации взвешенных сумм квадратов:
 .
.
