1. Содержание отчёта

• Титульный лист.

• Цель работы.

• Результаты выполнения индивидуального задания. В отчете должен быть представлен весь порядок выполненных вычислений.

• Выводы по работе.

Литература

1. Савельев А.Я. Основы информатики: Учеб. Для вузов.- М.: Изд-во МГТУ им. Н.Э.Баумана, 2001.- 328 с.

2. Лысиков Б.Г. Арифметические и логические основы цифровых автоматов. - Мн.: Высшая школа, 1980. -336 с.

3. Савельев А.Я. Прикладная теория цифровых автоматов: Учеб.для вузов по спец.ЭВМ.- М: Высш. Шк., 1987.-272 с.

4. Приложение

Контрольный пример выполнения лабораторной лаботы

Предположим, что N группы (NGR) 4103; номер варианта (NV)13, номер бригады (NB) 9. Поэтому по табл.5 формируем числа : А1 = 453₁₀; А2 = 46₁₀; А3 = 41₁₀

W = A2, A3 = 46,41₁₀

1. Осуществляется перевод числа W = 46,41 в а) двоичную, б) восьмеричную и в) шестнадцатеричную СС. Причем обеспечить точность перевода для g=2 6 разрядов после запятой; для g=8, g=16 - два после запятой.

а) 46 2

46 23 2 0 , 41

2

0 22 11 2 0 , 82

2

1 10 5 2 0 , 64

2

1 4 2 2 1 , 28

2

1 2 1 2 0 , 56

2

0 0 0 1 , 12

2

1 0 , 24

2

0 , 48

При переводе дроби получаем 7 разрядов после запятой, и по значению 7-ого разряда округляем 6-ой.

Ответ: W=46,41₁₀ ~101110,011010₂

б)

46 8

0 , 41

40 5 8 8

3 , 28

6 0 0 8

2 , 24 W=46,41₁₀ ~56,32₈

5 8

1 , 92

Если же воспользоваться связью двоичной и восьмеричной СС и осуществить перевод по триадам, то имеем

W = 46,41₁₀ = 101110, 011010₂ = 56,32₈

Ответ: W = 46,41₁₀ = 56,32₈

б)	46	16			0	41
	32	2	16			16	W = 46,4110 = 2E,6816
	E	0	0		6	56
		2				16
					8	96

Если воспользоваться связью двоичной и шестнадцатеричной СС и осуществить перевод по тетрадам, то имеем

W = 46,41₁₀ = 101110,011010₂ =2 E,68₁₆

Ответ: W = 46,41₁₀ = 2E,68₁₆

2. Перевести число А1 в а) восьмеричную и шестнадцатеричную СС; б) полученные числа представить в формате для целых чисел с фиксированной запятой; в) перевести число +А1_8,16, -А1_8,16 в дополнительный код.

а) А1 = 453₁₀ = 705₈ = 1С5₁₆

б) Пусть имеем разрядную сетку следующего вида :

4	3	2	1	0
знак	83	82	81	80
	163	162	161	160

старший разряд отводится под знак и с 0 по 3-ый разряды цифровой части числа.

Ответ:

0

0

7

0

5

;

0

0

1

С

5

в) +А1 = +705₈

-А1 = -705₈

Если для цифровой части числа отвести 4 разряда ,то имеем

[+А1]_доп = 0,0705

[-А1]_доп = 1,7072+0,0001 = 1,7073

+А1 = +1С5₁₆

-А1 = -1С5₁₆

Если для цифровой части числа отвести 4 разряда ,то имеем

[+А1]_доп = 0,01С5

[-А1]_доп = 1,FE3B+0,0001 = 1,FE3C

3. Выполнить над числами А2 и А3 следующие операции :

а) (А2+А3); б) (А2-А3); в) (-А2+А3); г) (-А2-А3).

Число представленное в форме с фиксированной запятой, является правильными дробями (т.е. 0,А2 и 0,А3) и записывается в форме

0 знак	1	2	3	4	5	6
	2-1	2-2	2-3	2-4	2-5	2-6

0,А2 = 0,46₁₀ = 0,011101₂ 0,А3 = 0,41₁₀ = 0,011010₂

а)

[+0,А2]_доп = 0,011101

+ Ответ:[А _сумм]_пр =[А _сумм] _доп =0,110111

[+0,А3] _доп = 0,011010

[А _сумм] _доп = 0,110111

б) [+0,А2]_доп = 0,011101

+ Ответ:[А _сумм]_пр =[А _сумм] _доп =0,000011

[-0,А3]_доп = 1,100110

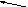
[А_сумм]_доп = 10,000011 гасится

в) [-0,А2]_доп = 1,100011

+ Ответ: [А _сумм] _доп= 1,111101

[+0,А3]_доп = 0,011010 [А _сумм]_пр= 1,000011

[А _сумм]_доп = 1,111101

г) [-0,А2]_доп = 1,100011

+ Ответ: [А _сумм]_доп = 1.001001

[-0,А3]_доп = 1,100110 [А _сумма]_пр = 1.110111

[А _сумм] = 11,001001

гасится

Ситуации переполнения разрядной сетки не были.

4. Выполнить над числами А1 и А2, которые являются целыми, беззнаковыми, представленными в шестнадцатеричной СС следующие операции в дополнительном коде:

а) (А1+А2); б) (А1-А2); в) (-А1+А2); г) (-А1-А2)

А1 = 453₁₀ = 1С5₁₆; А2 = 46₁₀ = 2Е₁₆

Если под цифровую часть чисел отводится 3 разряда, то имеем:

а) [+А1]_доп = 01С5

+ Ответ: :[А _сумм]_пр =[А _сумм] _доп =01F3₁₆

[+А2]_доп = 002Е А _сумм = 1F3₁₆

[А_сумм]_доп= 01F3

б) [+А1]_доп = 01С5

+ Ответ: :[А _сумм]_пр =[А _сумм] _доп.=0197₁₆

[-А2]_доп = 1F2 А_сумм=197₁₆

[А_сумма]_доп = 10197

гасится

в) [-А1]_доп = 1Е3В

+ Ответ: [А _сумм] _доп= 1Е69; : [А_сумм]_пр = 1197₁₆

[+А2]_доп = 002Е А_сумм = -197₁₆

[А_сумм]_доп = 1Е69

г) [-А1]_доп = 1.Е3В

+ Ответ: [А _сумм] _доп= 1Е1D₁₆; [А_сумм]_пр = 11F3₁₆

[-А2]_доп = 1.FD2 А_сумм = -1F3₁₆

[А_сумм]_доп = 11.Е1D

гасится

5. Найти произведение чисел А2 и А3 в двоичной СС, если А2 и А3 - целые числа без знака.

А2=46₁₀ = 101110₂ А3=41₁₀ =101001₂

0 0 0 0 0 0

+ 1 0 1 1 1 0

1 сумма 1 0 1 1 1 0

1 сдвиг 0 1 0 1 1 1 0

2 сдвиг 0 0 1 0 1 1 1 0

3 сдвиг 0 0 0 1 0 1 1 1 0

4 сумма + 1 0 1 1 1 0

1 1 0 0 1 1

4 сдвиг 0 1 1 0 0 1 1 1 1 0

5 сдвиг 0 0 1 1 0 0 1 1 1 1 0

5 сумма + 1 0 1 1 1 0

1 1 1 0 1 0

6 сдвиг 0 1 1 1 0 1 0 1 1 1 1 0

Ответ: А2хА3 = 11101011110₂ = 1886₁₀

6. Представить число W = 46.41₁₀ в форме с плавающей запятой в:

а) двоичной СС

б) восьмеричной СС

в) шестнадцатеричной СС,

Определить количество разрядов для представления порядка в этих СС.

а) W=46.41₁₀ = 101110,011010₂

W=0.101110011010*2⁶ = 0.101110011010 * 10^0.110

W=m*10 ^p . Для _представления р = +110 нужны 1 разряд под знак и три разряда под цифровую часть числа.

б) W=46.41₁₀ = 56.32₈

W=0.5632, (8)*8² = 0.5632*10^0.2

Для представления р = +2₈ нужен один разряд под знак и 1 разряд под цифровую часть числа

в) W=46.41₂ = 2E.68₁₆

W=0.2E68₁₆ * 16² = 0.2E68₁₆ * 10^0.2₁₆

Для представления р = +2₁₆ нужны один разряд под знак и 1 разряд под цифровую часть числа.