
Теория_КГ / Центральная Проекция_КГ
.docПЕРСПЕКТИВНЫЕ ПРОЕКЦИИ
Изображения, полученные при параллельном проецировании выглядят несколько нереально, что связано с сохранением параллельности прямых. Человек привык к перспективному изображению предметов. Эффект перспективы заключается в том, что параллельные прямые пересекаются на горизонте (рис.1). Предметы должны становиться меньше по мере их удаления от наблюдателя. Для достижения этого эффекта применяется центральное (перспективное) проецирование.

Рис. 1
Для описания перспективного изображения представим себе, что каждая видимая точка на объекте некоторой прямой линией (лучом) соединяется с глазом. При этом глаз видит лишь те предметы, что попадают в так называемый зрительный конус (на рис.1 это ABCDR ). Ось этого конуса совпадает с направлением взгляда.
Картинную плоскость мы помещаем перпендикулярно оси зрительного конуса. Чтобы построить перспективную проекцию, мы отмечаем точки пересечения лучей с этой плоскостью. Так как лучей бесконечно много, практически эта задача невыполнима. Но можно наносить на плоскость только те точки, что соответствуют важнейшим элементам объекта : вершины, концы отрезков, угловые точки граней и т. д..
Перспективное изображение получится, если мы соединим проекции этих точек таким же образом, как соединяются сами точки на объекте.
Свойства перспективной проекции:
1. Перспективная проекция прямой линии есть прямая линия.
2. Перспективная проекция грани (то есть плоской области, ограниченной замкнутой ломаной линией) есть грань. Если грань ограничена ломаной, состоящей из N сегментов, то и перспективная проекция этой грани будет гранью, ограниченной ломаной из N сегментов.
3. Проекция выпуклой грани есть выпуклая грань.
Классификация перспективных проекций определяется количеством точек схода проецирующих лучей для соответствующих осей X, Y, Z и приведена на рис.2

Точки схода образуют ребра объекта непараллельные картинной плоскости.
Рассмотрим теперь возможность описания перспективного проецирования с помощью однородных координат и матриц четвертого порядка.
Предположим для простоты, что центр проецирования лежит на оси Z в точке C(0,0,c), и плоскость проецирования (картинная плоскость) совпадает с координатной плоскостью XY (рис. 3). Возьмем в пространстве произвольную точку M(x, y, z), проведем через нее и точку C прямую. Соответствующие параметрические уравнения прямой есть:

x* = x t ; y* = y t ; z* = c + ( z - c ) t (1)
Найдем координаты точки пересечения построенной прямой с плоскостью XY. Из условия z* = 0 найдем значение параметра t:
t = 1 / ( 1 - z / c ) (2)
Тогда
x* = x / ( 1 - z / c ) ; y* = y / ( 1 - z / c ) ; ( 3 )
Заметим, что тот же самый результат можно получить, используя матрицу вида:

1 0 0 0
0 1 0 0
0 0 0 - 1 / c
0 0 0 1
А именно:

 1
0 0 0
1
0 0 0
( x y z 1 ) 0 1 0 0 = ( x y 0 1 - z / c ) (4)
0 0 0 - 1 / c
0 0 0 1
Учитывая свойства однородных координат, разделим все на
(1 - z / c):
( x / ( 1 - z / c ) y / ( 1 - z / c ) 0 1 ) (5)
То есть получили те же значения координат x* и y*, что и в формулах (3). Таким образом, вектор (5) - это однородные координаты точки (x y z 1) после выполнения операции перспективного проецирования, заданного матрицей:


1 0 0 0
Q = 0 1 0 0 (6)
0 0 0 - 1 / c
0 0 0 1
Матрица Q соответствует так называемому одноточечному перспективному преобразованию. Более сложные ( двухточечные и трехточечные) перспективные преобразования, представленные в классификации на рис.2, здесь не рассматриваются.
АЛГОРИТМ ВЫЧИСЛЕНИЯ ПЕРСПЕКТИВНОЙ ПРОЕКЦИИ
Учитывая все сказанное выше о перспективных проекциях можно отметить следующее:
1. Каждую вершину трехмерного объекта можно задать в однородных координатах в виде (x y z 1) и, следовательно, представить объект координатной моделью.
2. Перспективная проекция трехмерного объекта может быть получена с помощью матрицы Q.
3. После применения матрицы Q необходимо первую и вторую координаты разделить на последний элемент полученного вектора координат, то есть на (1 - z / c), чтобы получить координаты перспективной проекции точки на картинной плоскости.
ПРИМЕР ПОСТРОЕНИЯ ПЕРСПЕКТИВНОЙ ПРОЕКЦИИ
МНОГОГРАННИКА, ЗАДАННОГО СВОИМИ ВЕРШИНАМИ
Многогранник в трехмерном пространстве может быть задан координатами своих вершин. Эти координаты образуют матрицу координат, т.е. координатную модель многогранника.
Рассмотрим в качестве примера куб с длиной ребра, равной 2. Пусть необходимо сначала выполнить перенос куба по оси Z на величину z0 (рис.20), а затем получить перспективную проекцию этого объекта

Матрица, задающая координаты вершин исходного куба, имеет вид:

A -1 2 2 1
B 1 2 2 1
C -1 0 2 1
D 1 0 2 1
E -1 2 0 1
F 1 2 0 1
G -1 0 0 1
L 1 0 0 1
Для выполнения переноса используется матрица T , где = 0, = 0, = z0. Умножив матрицу координат вершин исходного куба на матрицу T, получим матрицу однородных координат вершин куба после переноса:
-1 2 2 1 -1 2 2+z0 1 A*
1 2 2 1 1 2 2+z0 1 B*
-1 0 2 1 1 0 0 0 -1 0 2+z0 1 C*
1 0 2 1 0 1 0 0 = 1 0 2+z0 1 D*
-1 2 0 1 0 0 1 0 -1 2 z0 1 E*
1 2 0 1 0 0 z0 1 1 2 z0 1 F*
-1 0 0 1 -1 0 z0 1 G*
1 0 0 1 1 0 z0 1 L*
Чтобы построить перспективную проекцию объекта, необходимо полученную матрицу умножить на матрицу Q:
-1 2 2+z0 1 -1 2 0 1 - (2+z0)/c
1 2 2+z0 1 1 2 0 1 - (2+z0)/c
-1 0 2+z0 1 1 0 0 0 -1 0 0 1 - (2+z0)/c
1 0 2+z0 1 0 1 0 0 = 1 0 0 1 - (2+z0)/c
-1 2 z0 1 0 0 0 -1/c -1 2 0 1 - z0/c
1 2 z0 1 0 0 0 1 1 2 0 1 - z0/c
-1 0 z0 1 -1 0 0 1 - z0/c
1 0 z0 1 1 0 0 1 - z0/c
Теперь необходимо 1-й и 2-й элементы каждой строки разделить на последний элемент этой же строки. Получим матрицу однородных координат перспективных проекций вершин куба, представленного на рис. 20 :

A* -1/ (1-(2+z0)/c) 2/ (1-(2+z0)/c) 0 1
B* 1/ (1-(2+z0)/c) 2/ (1-(2+z0)/c) 0 1
C* -1/ (1-(2+z0)/c) 0 0 1
D* 1/ (1-(2+z0)/c) 0 0 1
E* -1/ (1 - z0 / c ) 2/ (1 - z0 / c ) 0 1
F* 1/ (1 - z0 / c ) 2/ (1 - z0 / c ) 0 1
G* -1/ (1 - z0 / c ) 0 0 1
L* 1/ (1 - z0 / c ) 0 0 1
Перейдем теперь от однородных координат к обычным (для этого необходимо отбросить в матрице последний столбец), и вычислим значения элементов данной матрицы, например, при z0 = 2 и c = 8. Получим :
A* -2 4 0
B* 2 4 0
C* -2 0 0
D* 2 0 0
E* -4/3 8/3 0
F* 4/3 8/3 0
G* -4/3 0 0
L* 4/3 0 0
Это и есть координаты проекций вершин заданного куба (рис.20) на плоскость YX. Соединяя вершины прямыми, получим перспективное изображение куба (рис.21).
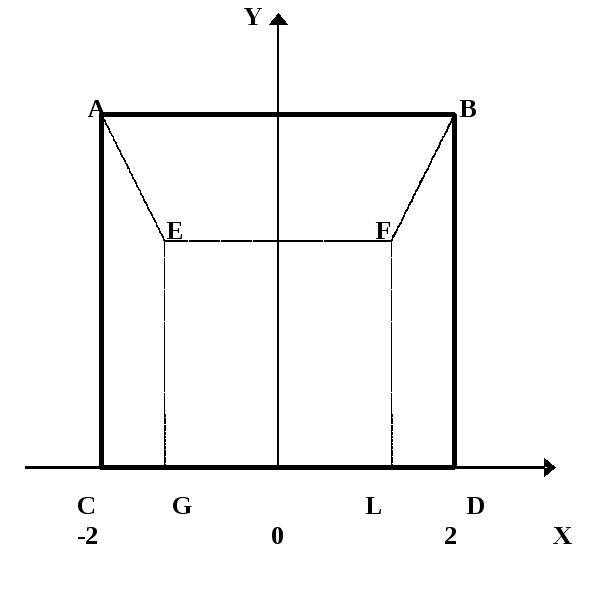
Рис. 21
