Теория_КГ / Отсечение по окну вывода_КГ

АЛГОРИТМЫ РЕШЕНИЯ ЗАДАЧИ ОТСЕЧЕНИЯ

Если изображение задано в системе координат окна видимости (физический экран дисплея, окно MS Windows, окно графического редактора), а затем масштабируется, поворачивается или сдвигается, то при выпол­нении преобразований возможен выход части изображения за пре­делы окна. Например, если изображение поворачивается на 45° по часовой стрелке относительно своего центра, то точка в верхнем правом углу окна будет преобразована в точку, расположенную несколько правее правой границы окна; отрезок, соединяющий ее с точкой в центре окна, будет располагаться частично в окне, а частично вне его.

В идеальном случае информация, подаваемая на дисплей, должна содержать лишь то, что отображается в окне видимости. Следовательно, необходимо иметь алгоритм отсечения для отбрасывания тех частей изображения, которые лежат за пре­делами окна.

ДВУМЕРНОЕ ОТСЕЧЕНИЕ

Н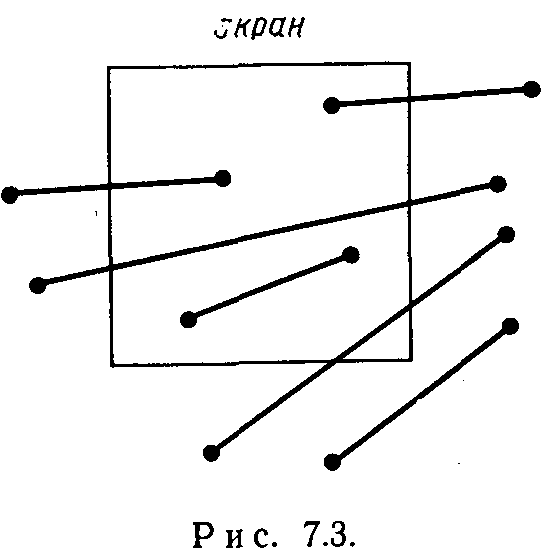а рис.7.3 показана плоская сцена и отсекающее окно регулярной формы. Регулярным отсекающим окном является прямоугольник, стороны которого параллельны осям координат мирового координатного пространства или осям координат экрана.

Целью алгоритма отсечения является определение тех точек, отрезков или их частей, которые лежат внутри окна. Эти точки, отрезки или их части остаются для визуализации, а все остальное отбрасывается.

Если бы все изображение задавалось как список точек, то от­сечение было бы весьма тривиальной задачей: всякая точка либо принималась для высвечивания, либо отбрасывалась путем срав­нения ее координат с координатами границ окна. Но не сущест­вует столь же простого способа, чтобы определить, попадает ли отрезок прямой или его часть в пределы окна. Если даже обе ко­нечные точки находятся вне окна, то отрезок может быть частично видимым: например, конечные точки могут располагаться вблизи про­тивоположных границ окна. На рис. 7.3 показан ряд различных положений, которые может занимать отрезок относительно окна. Следует заметить, что, поскольку окно имеет форму выпуклого многоугольника, при отсечении отрезка не может появиться более одного видимого участка. Видимая часть от­резка может быть однозначно определена своими двумя конечными точками; алгоритм отсечения должен лишь вычислить их координа­ты. Приводимый ниже алгоритм, разработанный Д. Коэном и А. Сазерлендом, позволяет не только очень быстро отыскивать указан­ные конечные точки, но еще быстрее отбрасывать все явно невидимые линии. В связи с этим данный алгоритм очень удобен для отсечения частей изображения, значительно выходящих за пределы экрана.

АЛГОРИТМ ОТСЕЧЕНИЯ ОТРЕЗКОВ КОЭНА-САЗЕРЛЕНДА

Алгоритм состоит из двух частей. Первая часть определяет; видим ли отрезок полностью в окне, и если нет, то можно ли его отбросить как полностью невидимый.

Если отрезок не удовлетворяет этим условиям, то он делится на две части, и прове­ряется, удовлетворяет ли каждая из этих частей этим условиям. Работа алгорит­ма основана на том, что каждый отрезок либо полностью лежит в пределах окна, либо его можно разделить так, чтобы одна из его частей могла быть отброшена .

Проверка на отбрасывание производится путем продления гра­ниц окна так, чтобы они разделили поверхность, на которой на­ходится полное изображение, на девять областей, как показано на рис.7.4

Каж­дой из этих областей присвоен четырехразрядный код, и две конеч­ные точки отрезка получают коды, соответствующие областям, в которых они находятся. Четыре разряда кода, если в них занесена единица, означают соответственно следующее:

• первый разряд: точка расположена левее окна;

• второй разряд: точка расположена правее окна;

• третий разряд: точка расположена ниже окна;

• четвертый разряд: точка расположена выше окна.

Очевидно, что если четырехразрядные коды для обоих концов отрезка равны нулю, то отрезок целиком лежит в пределах окна. Менее очевидно условие: если логическое пересечение этих двух кодов не равно нулю, то отрезок полностью располо­жен вне окна.

Если отрезок нельзя отбросить при одной из этих проверок, то его следует разделить на части. Простейший метод деления состоит в том, что находится точка пересечения отрезка с одной из границ окна и часть, лежащая вне окна, отбрасывается. Например, отрезок АВ на рис. 7.5 может быть разделен точкой С, и часть АС может быть отброшена. Получаем новый отрезок ВС, к которому применяются простейшие проверки на отбрасывание. Отрезок все еще не поддается простейшему отбрасыванию, поэтому он опять делится в точке D. Оказывается, что полученный отрезок ВD. Полностью лежит в пределах окна. Не всегда легко определить, где следует производить деление вначале - в точке С или в D, но если проверку на отбрасывание повторять, то порядок, в котором произ­водится деление, не влияет на конечный результат.

АЛГОРИТМ ДЕЛЕНИЯ СРЕДНЕЙ ТОЧКОЙ

Отрезок можно разделить средней точкой и таким путем обой­тись без непосредственного определения точек пересечения отрез­ка с границами окна. Вариант алгоритма с делением средней точкой можно свести к двоичному поиску и реализовать аппаратно или микропрограммно.

Первая часть алгоритма, определяющая видимые и тривиально невидимые отрезки остается неизменной. При выполне­нии второй части отрезок делится средней точкой пополам на два участка. Затем алгоритм применяется к каждому из этих участков со следующими ограничениями:

1. Один из концов исходного отрезка может оказаться видимым (рис. 7.6, отрезки А и В). В этом случае одна из его половин либо полностью видима (отрезок А), либо отбрасывается по простейшему правилу (отрезок В). Тогда алгоритм применяется к другой половине отрезка.

2. Если обе конечные точки исходного отрезка невидимы (рис. 7.6, отрезки С, D и Е), то каждая из половин рассматривается отдельно. Обе половины могут быть отброшены по простейшим пра­вилам (отрезок С), в этом случае невидим весь отрезок. В другом случае по простейшим правилам может быть отброшен один участок (отрезок D); в третьем случае средняя точка видима, и ни одну из половин нельзя отбросить (отрезок Е). В этом случае алгоритм при­меняется к обеим половинам.

Эффект описанного процесса деления состоит в том, что осуще­ствляется логарифмический поиск конечных точек видимой части отрезка. Поиск конечных точек прекращается, когда отбрасывают­ся обе половины или когда средняя точка совпадает с одной из границ окна. Максимально необходимое количество делений равно максимальному количеству двоичных разрядов, используемых для представления координат х и у.

ТРЕХМЕРНОЕ ОТСЕЧЕНИЕ

Двумя наиболее распространенными формами трехмерных видимых объемов являются: прямоугольный параллелепипед (полый брусок), используемый при параллельном проецировании и усеченная пирамида – при центральном проецировании. Как и при двумерном отсечении, отрезки, которые полностью видимы или тривиально невидимы, можно идентифицировать с использованием обобщения кодов концевых точек отрезка Коэна-Сазерленда.

Но в трехмерном случае используется 6-битовый код, в котором 5-й и 6-й биты учитывают положение концевых точек отрезков ближе и дальше границ видимого объема. Точно также в биты кода заносятся единицы и нули с помощью обобщения двумерной процедуры. Точно так же, если побитное логическое произведение кодов концов отрезка не равно нулю, то он полностью невидим. Если же логическое произведение равно нулю, то отрезок может оказаться как частично видимым, так и полностью невидимым. В этом случае необходимо определять пересечения отрезка с гранями видимого объема.