радиолокационные системы / Динамические характеристики линейного элемента

Динамические характеристики линейного элемента

Линейным называют элемент, обладающий следующим свойством. Если при входных воздействиях x₁(t) и x₂(t) выходная величина меняется как y₁(t) и y₂(t) соответственно, то при воздействии x₁(t) + x₂(t) выходная величина меняется как y₁(t) + y₂(t). Другими словами, реакции на любое число внешних воздействий можно складывать независимо друг от друга (свойство суперпозиции), а изменение масштаба входной величины пропорционально меняет выходную величину, не оказывая влияния на ее вид (свойство гомогенности).

Гармонический сигнал, проходя через линейный элемент, изменяет свою амплитуду и фазу, а частота сигнала сохраняется. Изменения амплитуды и фазы зависят от частоты:

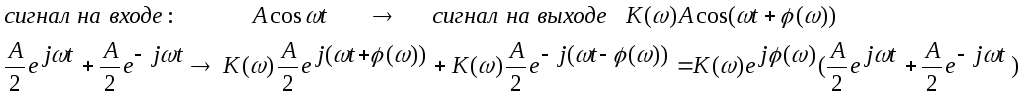В комплексном представлении гармонический сигнал на выходе элемента получается умножением входного гармонического сигнала на комплексный коэффициент передачи элемента

Это утверждение справедливо для каждой спектральной составляющей сигнала. Следовательно, спектр выходного сигнала равен спектру входного сигнала, умноженному на комплексный коэффициент передачи элемента.

Функцию К(ω), обозначаемую часто как А(ω), называют амплитудно-частотной характеристикой элемента, а функцию φ(ω) – фазочастотной характеристикой.

Реакцию элемента на δ-импульс называют импульсной характеристикой w(t), или весовой функцией. Спектр δ-импульса равномерный, поэтому спектр импульсной характеристики совпадет по форме с комплексным коэффициентом передачи элемента. Комплексный коэффициент передачи элемента является спектром импульсной характеристики.

Реакцию y(t) элемента на сигнал х(t) произвольной формы можно определить, зная импульсную характеристику w(t):

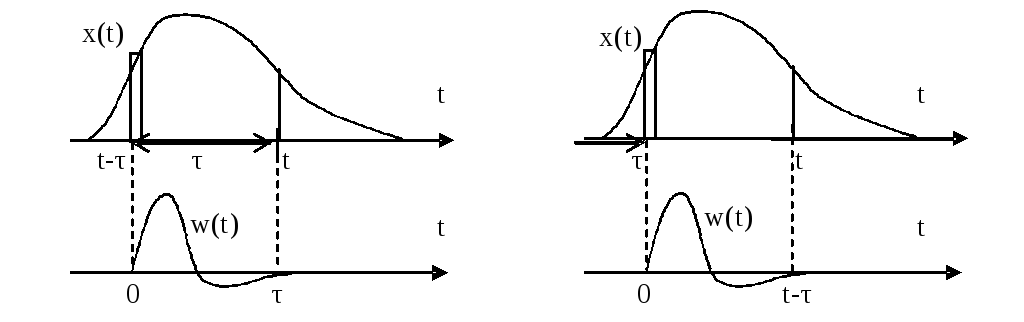
Это выражение называют сверткой функций х(t) и w(t), или интегралом Дюамеля.

Следствия преобразования Фурье

С уменьшением длительности сигнала его спектр расширяется. Это видно из примера спектра прямоугольного импульса.

П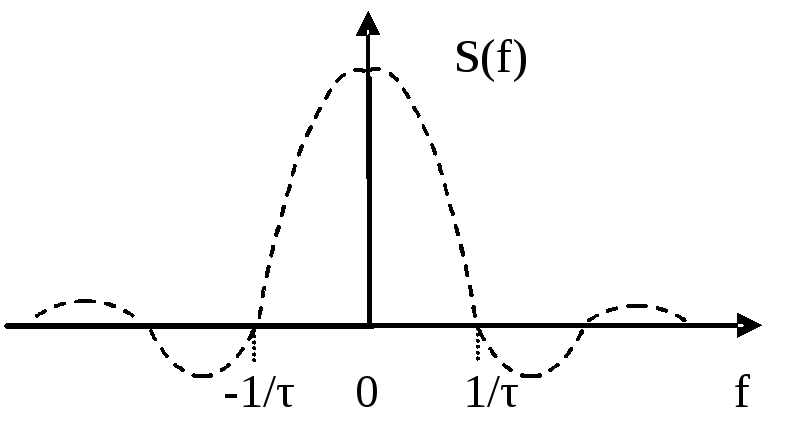роизведение длительности сигнала на ширину его частотной полосы называют базой сигнала. У видеоимпульсов база порядка 1 (ширина спектра прямоугольного импульса длительности τ, по первому лепестку в области положительных частот, равна 1/τ). Спектр прямоугольного импульса длительности τ при τ→0 становится равномерным на всех частотах от -∞ до +∞, а сам импульс превращается в δ-функцию.

Спектральная функция δ – импульса постоянна на всех частотах

В формулах прямого и обратного преобразования Фурье

п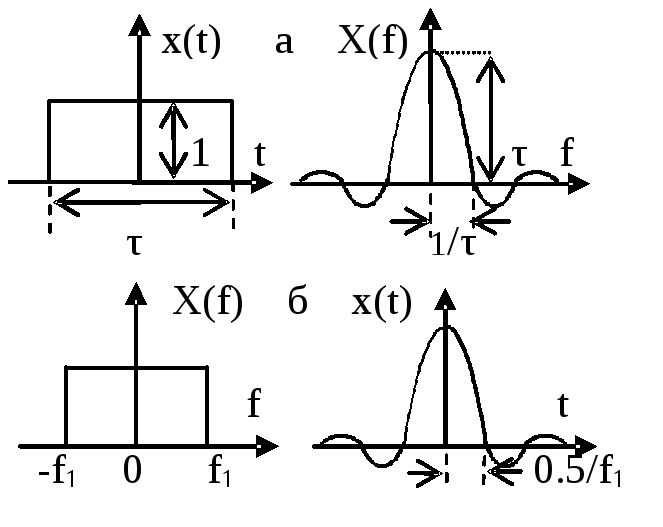еременные t и f взаимозаменяемые. Прямоугольный импульс имеет бесконечный спектр вида sinx/x (а). Заменив, на рис.(а), t на f , а f на t, увидим, что прямоугольный спектр соответствует импульсу вида sinx/x, длящемуся от -∞ до +∞ (б).

Следовательно, фильтр с прямоугольной частотной характеристикой неосуществим, т.к. он должен превращать δ – импульс в импульс, начинающийся при t = -∞.

Спектральная функция Y(f) выходного сигнала элемента равна произведению спектральной функции X(f) входного сигнала и комплексного коэффициента передачи элемента W(f), а выходной сигнал y(t) элемента – это свертка входного сигнала x(t) и импульсной характеристики w(t):

Заменив t на f , а f на t в выражениях Y(f) и y(t), получим

т.е.

спектр произведения сигналов равен свертке спектральных функций сигналов.

Спектр произведения сигналов

Спектр произведения двух гармонических сигналов следует из тождества

Спектр произведения двух сигналов можно получить, заменив каждую спектральную линию ω_i одного сигнала спектром другого сигнала, расположенным симметрично относительно частоты ω_i

Спектр радиоимпульса:

При модуляции высокочастотного гармонического сигнала спектр модулирующего сигнала переносится в область высоких частот с расширением полосы в два раза.

Спектр пачки импульсов:

Спектр последовательности

амплитудно – модулированных радиоимпульсов

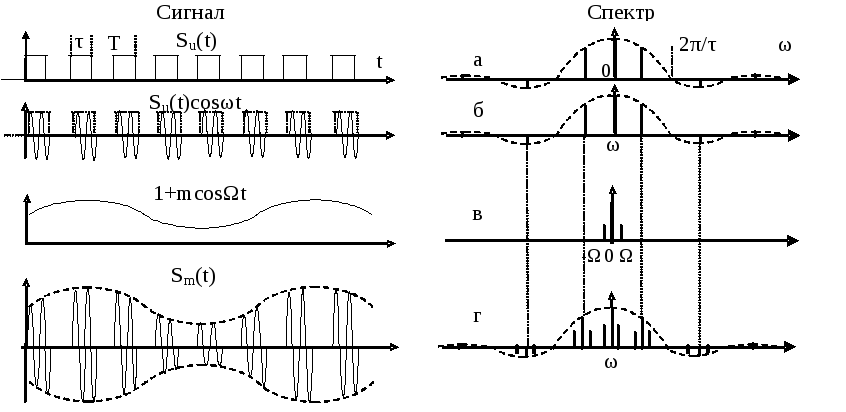
Спектр (б) последовательности радиоимпульсов – сигнала S_u(t)cosωt - получается переносом спектра (а) последовательности импульсов S_u(t) в область высоких частот – в окрестность частоты ω.

Спектр (г) сигнала S_m(t) получается заменой каждой линии спектра (б) спектром (в) сигнала (1+mcosωt).