Реализация
Разработанные алгоритмы реализуют, составляя по ним текст программы с использованием конкретного языка программирования. Язык может быть определен в техническом задании, а может выбираться исходя из особенностей конкретной разработки.
Тестирование разработанных программных модулей
Тестированием называют процесс выполнения программы при различных тестовых наборах данных с целью обнаружения ошибок. Правильный подбор тестовых данных - отдельная и достаточно сложная задача. Для поиска логических ошибок также можно использовать отладчик - по шагам отследить процесс получения результата. Однако полезно бывает выполнить программу вручную, фиксируя результаты выполнения команд на бумаге. При этом очень поможет пример расчета, выполненный вручную на этапе анализа и выбора методов.
Параллельно с процессом разработки программного продукта на всех этапах должно выполняться составление документации, как для выполнения следующего этапа, так и для последующего сопровождения и модификации.
Пример разработки алгоритма
Для разработки алгоритма в структурном программировании эффективно использование метода пошаговой детализации.
Создание программы - процесс сложный, поэтому практически с любого этапа возможен возврат на предыдущие этапы для исправления ошибок или принятия других проектных решений. Чаще всего такого рода возвраты являются следствием ошибок, допущенных при логическом проектировании программы. Поэтому в процессе программирования необходимо особое внимание уделять разработке алгоритмов.
С использованием метода пошаговой детализации разработку алгоритмов выполняют поэтапно. На первом этапе описывают решение поставленной задачи, выделяя подзадачи и считая их решенными. На следующем аналогично описывают решение подзадач, формулируя уже подзадачи следующего уровня. Процесс продолжают до тех пор, пока не дойдут до подзадач, алгоритм решения которых очевиден. При этом, описывая решение каждой задачи, желательно использовать не более одной-двух конструкций, таких как цикл или ветвление, чтобы четче представлять структуру программы.
Для разработки алгоритма программы, которая находит значение аргумента х по заданному значению функции у(x).
Определяем общую структуру программы.
Начало
Ввести выражение для функции
Ввести у, n, E.
Вывести график функции
Определить х.
Вывести x, у.
Конец
Детализируем операцию определения х.
Определить х:
Определить х1 такое, что f(xl) < у.
Определить х2 такое, что f(x2) > у.
Определить х на интервале [х1, х2].
Конец.
Детализируем операцию определения х1.
Значение х1 должно быть подобрано так, чтобы выполнялось условие f(xl) < у. Известно, что x > 0, следовательно, можно взять некоторое значение х, например, х1=1, и последовательно уменьшая его, например в два раза, определить значение х1, удовлетворяющее данному условию.
Определить х1:
х1 := Xm;
цикл-пока f(xl) > у
х1 := х1/2;
конец-цикла
Конец.
Детализируем операцию определения х2.
Значение х2 определяем аналогично х1, но исходное значение будем увеличивать в два раза.
Определить х2:
х2 := 0.1;
цикл-пока f(x2) < у
х2 := х2*2;
конец-цикла
Конец.
Детализируем операцию определения х.
Определение х выполняется последовательным сокращением отрезка [х1, х2].
Определить х:
цикл-пока (x2 – x1) > E
Сократить отрезок [х1, х2].
конец-цикла
Конец.
Детализируем операцию сокращения интервала определения х.
Сокращение отрезка достигается делением пополам и отбрасыванием половины, не удовлетворяющей условию f(x1) <= у<= f(x2).
Сократить интервал определения х:
xt:=(xl +х2)/2
если f(xt) > у
то х2 := xt,
иначе х1 :=xt.
конец-если
Конец.
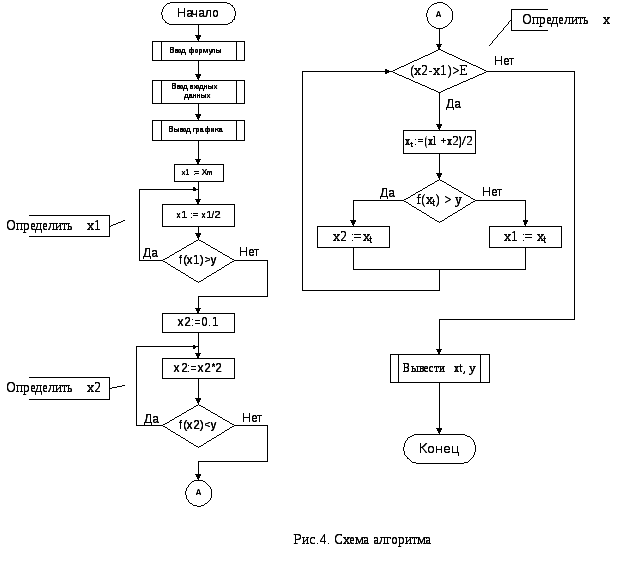
Таким образом, за шесть шагов мы разработали весь алгоритм, который выглядит следующим образом.
Программа
Начало:
Ввести выражение для функции
Ввести у, n, E
Вывести график функции
% Определить х1:
х1:=Xm;
цикл-пока f(xl) > у
х1:=х1/2;
конец-цикла
% Определить х2:
х2:=0.1;
цикл-пока f(x2) < у
х2 := х2*2;
конец-цикла
% Определить х:
цикл-пока (х2-х1) > E
xt:=(xl +х2)/2
если f(xt) > у
то х2 := xt
иначе х1 := xt
конец-если
конец -цикла
Вывести xt, у.
Конец.
В приведенном тексте строка, начинающаяся с символа «%» - комментарии, не влияющие на порядок вычислений и необходимые для лучшего понимания текста.
Таким образом, на каждом шаге решается одна достаточно простая задача, что существенно облегчает разработку алгоритма и является основным достоинством метода пошаговой детализации.
При разработке алгоритма методом пошаговой детализации мы использовали псевдокод, но можно было использовать и схемы алгоритма, в которых решение каждой подзадачи может быть обозначено блоком «предопределенный процесс», однако это не обязательно.
Общая схема алгоритма приведена на рис.4. Далее необходимо детализировать выполнение подзадач ввода и вывода.
