Виноград(Вектор_управ_АД)321стр

Основным недостатком синусоидальной ШИМ, формируемой методом сравнения, является невысокий коэффициент использования напряжения питания. Он определяется соотношением

Uлm = 23 Ud ,

где U лm — максимальное значение амплитуды линейного выходного

напряжения инвертора. Реальное значение выходного напряжения инвертора будет еще ниже из-за ограничения минимальной величины импульсов управления инвертором.

С целью повысить коэффициент использования напряжения применяются так называемые модифицированные ШИМ, отличающиеся от базовой синусоидальной ШИМ наличием блока предварительной модуляции (предмодуляции). В состав этого блока (рис.7.3) входят генератор сигнала предмодуляции и три сумматора этого сигнала с задающими воздействиями на входах системы управления. Одним из эффективных и вместе с тем относительно несложных в реализации способов предмодуляции является предмодуляция путем введения третьей гармоники в сигналы задания с амплитудой

Uпm = 16U zm′ .

Рис.7.3. Схема блока предмодуляции

Иллюстрация данного способа представлена на рис.7.4. Использование предмодуляции позволяет повысить коэффициент

использования напряжения в режиме максимального неискаженного выхода теоретически до 1 (U лm =Ud ) и снизить величину пульсаций электромагнитного момента и тока статора на 10—12 %.

101

Общими недостатками формирования ШИМ путем сравнения сигналов управления с опорным являются:

1)ориентация на реализацию средствами аналоговой элементной базы;

2)повышенная сложность реализации при необходимости получить высокий коэффициент использования источника питания;

3)недостаточная гибкость для синтеза оптимальных законов коммутации ключей инвертора в различных режимах работы привода.

Указанных недостатков лишен векторный метод формирования ШИМ.

7.2. Принципы построения векторных широтно-импульсных модуляторов

Методология построения векторных модуляторов базируется на векторном представлении совокупности выходных напряжений инвертора и ориентирована на микропроцессорную реализацию.

Первоначально предположим, что ключи инвертора напряжения, относящиеся к одной фазе нагрузки, работают строго в противофазе и переключаются мгновенно. В этом случае инвертор можно представить в виде трех двухпозиционных ключей (рис.7.5), каждый из которых подключает соответствующую фазу нагрузки либо к положительному, либо к отрицательному полюсу источника постоянного напря-

жения Ud в зависимости от трехмерного вектора входных сигналов

управления. Всего имеется 23 =8 возможных состояний ключей инвертора. Векторы выходных напряжений инвертора, соответствующие

102

всем возможным его состояниям, представлены на векторной диаграммеr r рис.7.6. Имеется шесть значащих (отличных от нуля) векторов

U1...U6

фаз нагрузки к отрицательному либо к положительному полюсу источника.

Эти векторы будем называть образующими векторами. В случае симметрии нагрузки все ненулевые образующие векторы имеют одинаковые амплитуды:

U1 =U2 =U3 =U4 =U5 =U6 = 23Ud .

Каждый вектор однозначно характеризуется своим трехразрядным двоичным кодом состояния.

Под алгоритмом формирования выходного напряжения инвертора будем пониматьr последовательность включения образующих векторов

напряжения Uk , k =1...8

соотношениямиr . Введем понятие вектора эквивалентного напряжения

инвертора Uэкв , представляющего собой вектор выходного напряже-

ния, усредненного на временном интервале дискретности управления инвертором. Задачей любого алгоритма является формирование в нагрузке заданного значения вектора эквивалентного напряжения. Каждый алгоритм однозначно характеризуется своей элементарной ком-

бинацией векторов напряжения Uk , формирующих элементарный

цикл переключения ключей инвертора. Весь алгоритм складывается из совокупности повторяющихся элементарных циклов.

103

Математически задачу векторного формирования алгоритма можно сформулировать в виде следующего выражения:

где Tц — период цикла модуляции (продолжительность элементарной комбинации векторов); Ui — i-й вектор, входящий в элементарную

комбинацию; Ti ,τi = Ti — абсолютная и относительная продолжи-

Tц

тельности включения i-го вектора напряжения.

Постановку задачи в виде (7.1) дополним ограничениями, следующими из физического смысла задачи:

i=1

где n — общее число векторов напряжения в элементарной комбинации векторов.

Формирование одного и того же вектора эквивалентного напряжения может осуществляться множеством различных элементарных комбинаций выходных векторов инвертора, то есть в рамках различных алгоритмов управления. При этом алгоритмы будут отличаться друг от друга следующими показателями:

-величиной пульсаций тока в фазах нагрузки;

-потерями, обусловленными дискретностью работы инвертора;

-коэффициентом использования источника напряжения;

-числом коммутаций ключей инвертора за период модуляции;

-коэффициентом использования нагрузочной способности ключей инвертора по напряжению;

-степенью симметрии управления фазами инвертора.

Критерии синтеза, полученные на основе этих показателей в большей части являются противоречащими друг другу. Синтез алгоритма (выбор элементарной комбинации векторов напряжения) может выполняться на основе требования оптимального сочетания указанных показателей, задаваемого в каждом конкретном случае с помощью весовых коэффициентов.

В общем случае задача синтеза векторных ШИМ включает следующие основные этапы:

1)предварительный анализ координат заданного вектора эквивалентного напряжения и при необходимости их ограничение для обеспечения принципиальной возможности решения задачи синтеза;

104

2)выбор состава элементарной комбинации образующих векторов для формирования заданного вектора с учетом его пространственного положения;

3)определение длительностей интервалов включения каждого из образующих векторов в пределах периода модуляции (усреднения) в соответствии с требованием равенства усредненного значения вектора напряжений инвертора заданному значению;

4)выбор порядка включения образующих векторов в элементарной комбинации и синтез сигналов управления ключами инвертора во временной области.

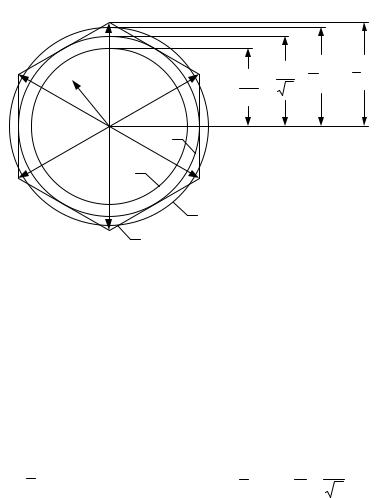
Рис.7.7. К оценке граничных режимов управления инвертором при различных вариантах ШИМ

Физические ограничения на величину заданного вектора эквивалентного напряжения легко определяются из анализа векторной диаграммы выходных напряжений инвертора (рис.7.7). Из анализа следует:

1)задача формирования заданного вектора эквивалентного напряжения

физически реализуема, если этот вектор находится в пределах шестиугольника, образованного векторами Ur1...Ur6 (линия 2);

2)предельное значение модуля формируемого вектора является функцией его углового положения: оно максимально на границах секторов ( 23Ud ) и минимально в их середине ( 23Ud cos π6 = U3d );

105

3)при векторной модуляции по синусоидальному закону амплитуда фазного напряжения ограничена значением U s.ф.гр = U3d (линия 3).

Для сравнения векторной модуляции с другими способами формирования сигналов на выходе инвертора на рис.7.7 показан также годограф граничного вектора при традиционной синусоидальной ШИМ с

пилообразным опорным сигналом (окружность 4 с радиусом Ud 2 ) и

годограф основной гармоники вектора фазных напряжений при шестиступенчатом алгоритме управления без ШИМ (окружность 1 с радиу-

сом 2Ud π ).

При выборе состава элементарной комбинации векторов напряжения в векторных ШИМ типовым решением является выбор трех векторов, образующих сектор, в котором находится заданный вектор эквивалентного напряжения, двух ненулевых и одного нулевого. Это позволяет получить алгоритмы, наиболее эффективные с точки зрения указанных выше критериев. Например, треугольный алгоритм, реализующий в первом секторе векторной диаграммы напряжений элементарную комбинацию вида

U1U2U8U2U1U7

Tц/2 Tц/2

Tц

Во втором секторе векторной диаграммы элементарная комбинация образующихr r векторов будет иметь вид

→U2 →U3 →U7 →U3 →U2 →U8 →.

Аналогичным образом элементарные комбинации формируются в других секторах. Для минимизации числа переключений инвертора последовательность включения векторов выбирается таким образом, чтобы каждый переход к новому состоянию сопровождался коммутацией только одной фазы инвертора. Именно поэтому после ненулевого

вектора U2 (110) включается нулевой вектор U8 (111) , а после ненулевого вектора U1(100) нулевой вектор Ur7 (000) .

Рассмотрим расчет продолжительности включения векторов напряжения при произвольном положении заданного вектора эквива-

106

где U = 32Ud — модуль ненулевых образующих векторов напряже-

ния; γu1 ,γu 2 — углы поворота образующих векторов относительно

оси α.

Решая это уравнение, получим:

С учетом ограничения на минимальную ширину импульса управления фазой инвертора tmin при выполнении условия t3 < tmin значе-

ния t1 ,t2 ,t3 корректируются следующим образом:

108

109

Время включения одинаковых образующих векторов напряжения равномерно распределяется в соответствии с их числом в пределах периода модуляции. При отсчете начала периода и полупериода модуляции от центра интервала включения нулевого вектора импульсы управления оказываются расположенными симметрично относительно точек отсчета (отсюда происходит распространенное в литературе название – центрированная ШИМ). Заметим, что в силу симметрии ШИМ обновление задания вектора напряжения может выполняться один раз за полный период либо один раз за полупериод модуляции.

Импульсы управления фазами инвертора распределяются по шести его ключам с учетом формирования защитных временных задержек между коммутациями ключей одной фазы.

7.3. Понятие об асинхронных и синхронных ШИМ

Важным показателем, характеризующим алгоритм управления, является коэффициент модуляции, представляющий собой отношение частоты модуляции к частоте основной гармоники выходного напряжения инвертора:

ния. Для треугольной центрированной ШИМ Tm =Tц 2 .

Если в заданном диапазоне изменения частоты fu1 коэффициент модуляции принимает только целые значения, то алгоритм модуляции в этом диапазоне частот называют синхронным. Если Km при измене-

нии fu1 способен принимать дробные значения, то алгоритм модуля-

ции называют асинхронным.

Асинхронные алгоритмы наиболее просты в реализации, их частота модуляции принимается постоянной и не изменяется с изменением частоты основной гармоники напряжения. Общим недостатком таких алгоритмов является наличие в выходном напряжении инвертора субгармонических составляющих, которые появляются при дробных зна-

чениях Km . При определенных условиях они могут приводить к пол-

ной неработоспособности электропривода, проявляющейся в низкочастотных биениях его переменных. Подобные явления возникают, как правило, в частотных электроприводах, в которых отсутствует слежение за мгновенными значениями тока фаз статора. Эффект усиливает-

110