Квантовая физика. Лабораторный практикум

где ∆ – оператор Лапласа; må – масса электрона; ε0 – электрическая

постоянная; = h ; h – постоянная Планка; E – энергии стационар2π

ных состояний; Ψ – волновая функция электрона в атоме водорода. Квадрат модуля волновой функции Ψ 2 определяет вероятность нахождения электрона в заданном месте пространства.

Можно показать, что уравнение (2) имеет однозначные, конечные и непрерывные решения при любых положительных значениях E > 0, а также при дискретных отрицательных значениях энергии

ãäå R – постоянная Ридберга; c – скорость света в вакууме; n – главное квантовое число. Эти дискретные значения энергии определяют систему термов атома водорода. Волновые функции Ψ , являющиеся решениями уравнения (2), описывают возможные квантовые состояния электрона.

Состояние электрона в атоме водорода характеризуется тремя целыми квантовыми числами n, l è m.

Орбитальное квантовое число l определяет момент импульса электрона M = l(l + 1) , l = 0,1, 2,...,(n–1).

Состояния, соответствующие различным значениям орбитального числа l, обозначаются соответственно: s(l = 0), p(l = 1) , d(l = 2) , f(l = 3) è ò. ä.

Магнитное квантовое число m определяет проекцию момента им-

Если заданы квантовые числа n, l, m состояния электрона в атоме, то могут быть определены энергия, момент импульса и проекция момента импульса электрона в этом состоянии. Энергия электрона в атоме водорода зависит только от главного квантового числа n. Следовательно, каждому значению энергии En (кроме E1) соответствует несколько квантовых состояний, отличающихся значениями квантовых чисел l è m. Состояния с одинаковой энергией называются вырожденными, а число различных квантовых состояний с одинаковым значением энергии называют кратностью вырождения g соответствующего энергетического уровня.

Поскольку l всегда меньше n, возможны следующие состояния электрона в атоме в зависимости от n è l:

21

При обозначении квантового состояния главное квантовое число указывается перед условным (буквенным) обозначением квантового числа l.

Экспериментальное определение энергии уровней атома водорода и других атомов показывает, что уровней больше, чем предсказывает рассмотренная выше теория. Это расхождение связано с тем, что электрон, как и большинство других элементарных частиц, обладает собственным моментом s-спином.

Проекция спина sz, так же, как и проекция орбитального момен-

та, меняется дискретно на величину, кратную (4), sz = ± 1 = ms . 2

Величина ms = ± 1 называется спиновым квантовым числом. Сле-

2 довательно, для полного определения состояния электрона в атоме

необходимо задать четыре квантовых числа n, l, m è ms.

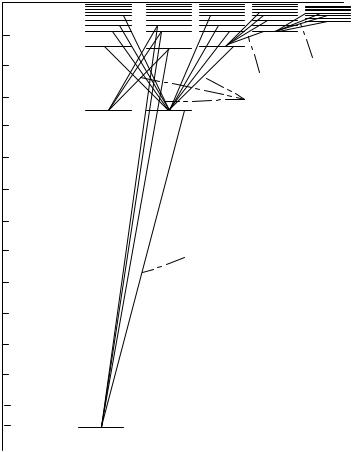
Схема энергетических уровней атома водорода и соответствующих переходов представлена на рис. 1. Горизонтальными отрезками линий изображены уровни энергий, которые здесь разбиты на пять рядов уровней, соответствующих различным значениям орбитального квантового числа электрона l. Цифра около линий, изображающих уровни энергий, дает значение главного квантового числа. Расстояние между уровнями по вертикали, пропорционально разности энергий между ними в эВ. На рис. 1 показаны переходы, разрешенные правилом отбора для орбитального квантового числа l(∆l = ±1) .

Правило отбора является следствием выполнения закона сохранения момента импульса при испускании кванта. Фотон также обладает собственным моментом-спином, равным 1 (в единицах ). При испускании фотон уносит из атома этот момент импульса, вследствие чего орбитальное квантовое число электрона l меняется на единицу.

Атомы большинства элементов представляют собой многоэлектронные системы. Атомные электроны находятся в усредненном электрическом поле, создаваемом ядром и остальными электронами. Состояние атома характеризуется квантовыми числами полного орби-

тального момента электронной оболочки L, полного спина S, à òàê-

же полного момента атома J = L + S . Квантовое число L принимает значения, отличающиеся друг от друга на 1 в пределах между (∑li )max è (∑li )min , аналогично значения квантового числа S лежат в преде-

22

ëàõ (∑ ms )max è (∑ ms )min . Для полностью заполненных оболочек L = 0 è S = 0.

Энергии Enl возбужденных состояний электрона в многоэлектронном атоме могут быть определены аналогично (3)

23

ãäå Zc – заряд атомного остова; n* – эффективное главное квантовое число возбужденного состояния n* = n − δl ; δl – называется квантовым дефектом. Величина квантового дефекта δl слабо зависит от n. Квантовый дефект δl характеризует отличие взаимодействия возбужденного электрона с атомным остовом от кулоновского (главным образом, за счет поляризации остова и обменного взаимодействия возбужденного электрона с внутренними электронами, обусловленного тождественностью электронов).

На рис. 2 показана схема энергетических уровней атома ртути. Цифры около горизонтальных отрезков дают значения главного квантового числа уровня энергии. Для наружного электрона атома ртути наименьшее значение квантового числа n = 6. Символами S,P,D,F обозначаются энергетические состояния атома с различными значе-

–10 6

Ðèñ. 2

24

ниями L (L = 0,1,2,3). Цифры под буквами S, P, D è F указывают

значение квантового числа J. Необходимость введения квантового

числа полного момента атома J = L + S связана с тем, что в результате релятивистских эффектов уровень с данными значениями L è S расщепляется на ряд уровней с различными значениями J. Об этом расщеплении говорят, как о тонкой структуре (или мультиплетном расщеплении) уровня; J может принимать значения от L + S äî L − S , поэтому уровень с данными значениями квантовых чисел L è S расщепляется на 2S + 1 (åñëè L > S) èëè 2L + 1 (åñëè L < S) различных подуровней.

В атоме с двумя валентными электронами полный спин может принимать два значения S = 0 è S = 1, так как каждый электрон

имеет спин s = 12 . Поэтому для двухвалентных элементов характер-

ны две системы уровней (см. рис. 2): система синглетных (одиноч- ных) уровней при S = 0; J = Lи система триплетных (тройных) уровней при S = 1; J = (L + 1), L, (L – 1). Верхний индекс над буквами S,P,D è F – “1” для синглетов и “3” для триплетов означает мультиплетность и равен 2S + 1. Переходы между энергетическими уровнями подчиняются правилам отбора для квантовых чисел J è L, которые гласят ∆J = 0,±1 ; ∆L = 0,±1 , причем переходы 0 → 0 запрещены.

Правилами отбора для атома ртути HgI разрешены, в частности

Справа внизу указаны значения J. Возможны также переходы между синглетными и триплетными уровнями. o

Длины волн переходов (рис. 2) указаны в ангстремах (1Α = 10−10ì ).

Описание лабораторной установки

Лабораторная установка состоит из гониометра, дифракционной решетки и ртутной лампы. Гониометр – это оптический прибор, предназначенный для измерения углов отклонения лучей с высокой точ- ностью. В работе используется гониометр типа Г-5. На массивном основании 1 (рис. 3) неподвижно установлен коллиматор 2, предназначенный для преобразования расходящегося пучка лучей в параллельный. Для наблюдения спектральных линий служит зрительная

25

4

12

15

1

13 14

Ðèñ. 3

труба 3, укрепленная вместе с окуляром отсчетного устройства 4 на корпусе подвижной части прибора – алидады 5. На входе коллиматора расположена раздвижная щель 6, перед которой устанавливается источник света. Зрительная труба имеет на выходе окуляр 7. В остальном конструкции 2 è 3 одинаковы. Фокусировка зрительной трубы и коллиматора производится с помощью маховиков 8.

На вертикальной оси прибора смонтирован столик 9, на который устанавливается дифракционная решетка. Столик можно поворачи- вать грубо от руки, отпустив зажимной винт 10, и точно с помощью микрометрического винта 11, предварительно зажав винт 10.

Порядок выполнения работы

1. Определяем длины волн спектральных линий

Длины волн спектральных линий определяют с помощью гониометра и дифракционной решетки. Если дифракционная решетка освещается немонохроматическим светом, то излучение разлагается в спектр. Длина волны спектральной линии может быть найдена, исходя из условия дифракционных максимумов

ãäå d – постоянная решетки; k – порядок спектра; ϕ – угол отклонения лучей.

26

73S1 → 63P0,1,2.

3. Проведем расчет энергии уровней тонкой структуры и определим длины волн триплетных переходов атомов ртути

Пользуясь схемой энергетических уровней атома ртути, зная потенциал ионизации Ui и.длину волны λ0 резонансного перехода 63P1 → 61S0 , определяем энергию E1 соответствующего нижнего состояния 63P1 . Значения Ui è λ0 указаны на установке.

27

Пользуясь формулой (1), рассчитываем энергию E2 состоя-

íèÿ 73S1 .

Зная энергию состояния73S1 и длины волн переходов73S1 → 63P0 è73S1 → 63P2 из данного состояния в состояния 63P0 è 63P2 , соответственно, определяют энергии этих уровней.

Вычисляют квантовый дефект δl äëÿ 7s -уровня по формуле (5)

4. Результаты измерений и расчетов заносим в табл. 1 и 2

Вычисления проводят как для переходов, указанных на схеме (рис. 2), так и для спектральных линий, длины волн которых были измерены.

28

Лабораторная работа ¹ 4

ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА

Цель работы: определение удельного заряда электрона при помощи электронно-лучевой трубки и магнетрона.

Методические указания

Удельным зарядом электрона называют величину, равную отношению величины электрического заряда электрона к его массе.

На движущийся в магнитном поле заряд действует магнитная сила Лоренца

В случае движения электрона ( q = e ) перпендикулярно магнитному полю уравнение (1) в скалярной форме перепишем следующим

èëè

Fë = 0evH,

òàê êàê B = 0H .

В вакууме и в воздухе относительная магнитная проницаемость

рона будет происходить по дуге окружности в плоскости, перпенди-

кулярной H .

Сила Лоренца играет роль центростремительной силы Fë = Fö è,

ãäå m – масса электрона; R – радиус дуги окружности.

29

Скорость электрона можно определить, зная ускоряющую разность потенциалов поля, в котором электрон разгоняется, приобретая кинетическую энергию

Из формул (3), (4) получаем

Формула (5) может быть использована для расчета удельного заряда электрона.

Описание лабораторной установки

Лабораторная работа состоит из двух частей. Каждая часть вы-

полняется на отдельном стенде, что позволяет определить величи- e

íó m двумя различными способами.

1. Определение удельного заряда электрона при помощи элект- ронно-лучевой трубки

Для получения пучка электронов и определения отклонения этого пучка в магнитном поле используется электронно-лучевая трубка, устройство которой схематически изображено на рис. 1, где K – оксидный катод, подогреваемый вольфрамовой нитью, расположенной внутри катода; ÔÀ – фокусирующий анод (венельтов цилиндр), служащий для формирования электронного пучка; À1 è À2 – аноды; ÔÝ – экран, покрытый слоем вещества, обладающего способностью светиться под воздействием катодных лучей.

Ðèñ. 1

Электроны, излучаемые катодом K, ускоряются электрическим полем в промежутке катод–аноды À1, À2 и, попадая на флюоресци-

30