
Kollesnikov - Лекции по электротехнике
.pdf
|
XL 2XC |
|
1L2 |
1 |
34arctg Х 4arctg |
4 arctg |
1c |
||
|
R |
|
||
R |
R |
|
||
– аргумент комплексного сопротивления цепи, определяет угол сдви га между током и напряжением на входе цепи.
Как видно из (2.36), общее комплексное сопротивление цепи при последовательном соединении элементов равно сумме комплексных сопротивлений отдельных элементов.
Исходя из (2.35) с учетом (2.36), можно записать закон Ома для цепи с последовательным соединением R, L, C
1 |
|
1 |
|
|
|
1 |
Um |
|
|
||
Im |
|
. |
(2.37) |
||
Z |
|||||
|
|
|
|
Построим векторную диаграмму. За опорный вектор выбираем век тор тока, так как ток один, соединение последовательное. Затем стро им векторы напряжений на каждом из элементов: на сопротивле
нииU1 |
, который совпадает по фазе с током, на индуктивностиU1 |
||||
mR |
1 |
|
|
mL |
|
|
|
|
|
||
– опережает, а на емкостиUmC – отстает от тока |
|
|
2 |
||
в цепи. Результирующий вектор – напряжение |
|
|
3 |
||
источника получаем в соответствии с ЗНК сум |
|
|
|
||
мированием векторов напряжений каждого эле |
2 |
|
|
||
11 |
|
|
|||
мента. |
|
|
2 |
||
|
2 |
|
112 |
||
Как видно из векторной диаграммы, для |
|||||
113 |
|
||||
цепи с последовательным соединением R, L, C |
2 |
|
2 |
||
(рис.2.18) характер цепи – индуктивный, так |
|
||||
114 |
113 |
||||
как ток отстает от входного напряжения на
угол . При этом соотношение между напряже |
Рис. 2.18 |
|
ниями на индуктивности и емкости:UmL 1 UmC , так как при построе нии векторной диаграммы для определенности приняли XL 1 XC .
Параллельное соединение G, L, C
Рассмотрим параллельное соединение G, L, C (рис. 2.19).
5 |
|
|
|
|
41 |
|
5 |
5 |
|
|
5 |
|||
|
412 |
413 |
||
5 |
414 |
|||
|
|
|||
|
|
|
||
31 |
1 |
2 |
1 |
Рис. 2.19
41
Обозначим токи элементов и составим ЗТК для верхнего узла
1 |
1 |
1 |
1 |
IGm |
1 ILm |
1 ICm |
2 Im. |
Выразим токи элементов в соответствии с законом Ома через на пряжение и проводимости, получим
1 1 1 1 1 2 1 .
UmYG UmYL UmYC Im
Обозначим через Y комплексную проводимость цепи
Y 1 YR 2 YL 2 YC 1 G 3 j(BL 3 BC) 1 G 3 jB 1 G2 2 (BL 3 BC)2e j4 1 ye j4,
(2.38)
(2.39)
где y 1 G2 2 (BL 3 BC)2 – полная проводимость, модуль комплексной проводимости цепи; 3 4 arctg BL 1 BC 4 arctg 21L 1 2C – угол сдвига
GG
между током и напряжением.
Как видно из (2.38), общая проводимость цепи при параллель ном соединении равна сумме проводимостей ветвей
Y 1 YR 2 YL 2 YC. |
(2.40) |
С учетом (2.39) из (2.38) закон Ома для цепи с параллельным со единением элементов G, L, C будет
1 |
1 |
(2.41) |
UmY 1 Im. |
||
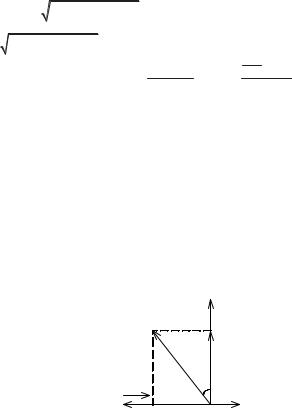
Построим векторную диаграмму для цепи: за опорный вектор бе рем напряжение, затем строим векторы токов для отдельных элемен тов с учетом углов фазового сдвига (2.5)–(2.7).Вектор входного тока
|
|
2 |
|
|
31 |
|
2 |
|
|
11 |
2 |
|
|
|
2 |
|
113 |
|
|
|
112 |
|
|
|
|
22
114 |
112 |
Рис. 2.20
получаем в соответствии с ЗТК путем сложения векторов токов парал лельных элементов. Как видно из векторной диаграммы для цепи с па раллельным соединением G, L, C (рис. 2.20), входной ток I1m опережает
42
напряжение U1m , т. е. характер цепи – активно емкостный.
2.9. Комплексное сопротивление и проводимость. Схема замещения двухполюсника на заданной частоте
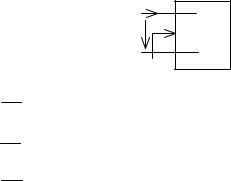
Рассмотрим некоторый двухполюсник, вклю |
4 |
|||
|
|
|
||
ченный на источник гармонического напряжения |
3 |
1 |
||
(рис. 2.21). |
1 |
|
3 |
|
1 |
на входе двух |
21 |
|
|
Зная напряжение Um и ток Im |
|
|
||
полюсника, найдем, соответственно, входное со |
112 |
|||
противление и проводимость |
|
|
||
|
1 |
|
|
Рис. 2.21 |
Z |
1 Um 1 R 2 jX, |
|
|
|
вх |
1 |
|
|
|
|
Im |
|
|
|
|
1 |
1 G 3 jB, |
|
|
Y |
1 Im |
|
|
|
вх |
1 |
|
|
|
|
Um |
|
|
|
Zвх 1 1 .
Yвх
Очевидно, что входное сопротивление и проводимость – обрат ные величины. Определим теперь, как связаны реактивное и ак тивное сопротивление с активной и реактивной проводимостью. Для этого помножим и разделим дробь на число сопряженное зна менателю и затем почленно разделим числитель на знаменатель (см. операцию деления комплексных чисел в алгебраической фор ме), получим
Z 2 |
1 |
2 |
G 1 jB |
2 |
|
|
G |
|
1 |
|
jB |
, |
||||||
|
|
|
|
G2 1 B2 |
G2 |
1 B2 |
||||||||||||
вх |
G 3 jB G2 1 B2 |
|
|
|
|
|
||||||||||||
|
R 2 |
|
|
|
|
G |
|
2 |
|
|
B |
|
|
|
|
|
||
|
|
|
|
|
, X |
|
|
|
|
|
|
|
(2.42) |
|||||
|
|
G |
2 |
2 |
G |
2 |
|
2 |
|
|
|
|||||||
|
|
|
|
|
1 B |
|
|
|
|
1 B |
|
|
||||||
– формулы перехода от параллельной схемы замещения двухполюс ника к последовательной.
Рассмотрим входную проводимость цепи и проделаем аналогич ные преобразования, получим
Y 2 |
1 |
2 |
1 |
2 |
|
R 1 jX |
2 |
|
R |
|
1 j |
|
X |
2 G 1 jB, |
||
|
|
R2 3 X2 |
R2 |
3 X2 |
|
R2 3 X2 |
||||||||||
вх |
Z R 3 jX |
|
|
|
|
|
|
|||||||||
|
вх |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
G 2 |
|
R |
|
, B 2 |
X |
|
|
|
(2.43) |
||||
|
|
|
R2 |
3 X2 |
|
R2 3 X2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
43

– формулы перехода от последовательной схемы замещения к парал лельной.
Следует отметить, что зная параметры одной схемы замещения воз можнонайтипараметрыдругойсхемытолькоприданнойчастоте,таккак висходнойцепичастотныехарактеристикиэлементовиветвейразличны.
|
3 |
|
|
3 |
|
|
|
|
|
|
|
a) |
21 |
|
б) |
21 |
|
|
|
|
|||
|
|
|
|
||
|
3 |
|
|
3 |
6 |
|
|
|
|
||
|
11 |
5 |
4 |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
Рис. 2.22 |
|
|
На рис. 2.22 показана параллельная схема замещения двухполюс ника (a) и последовательная схема замещения двухполюсника (б).
2.10. Анализ сложных цепей гармонического тока по законам Кирхгофа и методам токов связей
При анализе сложных цепей необходимо от цепи, содержащей сопротивления, емкости, индуктивности, источники, перейти к ком плексным сопротивлениям и комплексам амплитудных значений тока и напряжения, затем необходимо перерисовать цепь. Если не обращать внимание на точки и формально считать, что Z соответ ствует R, то для расчета цепей гармонического тока возможно ис пользовать все ранее рассмотренные методы расчета цепей постоян ного тока.
Пример
Составить уравнения для расчета цепи (рис. 2.23) по законам Кирх гофа методом токов связей и узловых напряжений.
5
 4 24132
4 24132
|
11 |
|
12 |
|
13 |
|
|
|
|
|
|
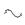 52
52
1
Рис. 2.23
44

Дано R1, C1, R2, L2, R3:
e2(t) 1 Em sin(2t 3 4), J4(t) 1 Im sin(2t 3 4).
Решение
1. Записываем комплексы амплитудных значений источников и сопротивлений ветвей
e2(t)2 1 |
2 |
1 |
1 Eme |
j11 |
, |
J4(t)2 1 |
2 |
1 |
1 Jme |
j14 |
, |
|
|
|
|||
|
E2m |
|
|
|
Jm |
|
|
|
|
||||||||
Z 1 R 2 jX 1 R 3 j |
|
|
1 |
, Z 1 R 2 jX 1 R 2 j4L , Z 1 R . |
|||||||||||||
|
|
|
|||||||||||||||
1 |
1 |
|
1 |
1 |
|
|
|
2 |
|
2 |
2 |
|
2 |
2 |
3 |
3 |
|
|
|
|
|
|
|
4C1 |
|
|
|
|
|
|
|
|
|||
2. Перерисовываем схему относительно комплексных значений сопротивлений и источников. Получим схему в виде (рис. 2.24).
2
431
22
421 411
12 |
11 |
|
2 |
21
2
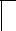
 13 31
13 31
1
Рис. 2.24
3. Рисуем граф цепи (рис. 2.25) и составляем уравнения по зако нам Кирхгофа:
|
1 |
|
1 |
1 |
|
|
12I1m |
3 I2m |
3 I3m 4 0, |
|
|||
5 |
1 |
|
1 |
|
1 |
|
6I1mZ1 |
3 I2mZ2 |
4 2E2m, |
|
|||
5 |
1 |
|
1 |
|
1 |
1 |
5I3mZ3 |
2 I2mZ2 |
4 J3mZ3 |
3 E2m. |
|||
7 |
|
|
|
|
|
|
2 |
2 |
2 |
1 |
12 |
13 |
Рис. 2.25
45
4. Получим систему уравнений относительно токов ветвей связей. Для этого выразим из ЗТК ток ветви дерева (ветвь 2) через токи вет вей связей:
1 |
1 |
1 |
I2m |
1 I1m |
2 I3m. |
Затем подставим это выражение в ЗНК и сгруппируем слагаемые с одинаковыми токами и получим
1 |
1 |
1 |
|
I1m(Z1 |
1 Z2) 2 I3mZ2 |
3 2E2m, |
|
1 |
1 |
1 |
1 |
I3m(Z3 |
1 Z2) 2 I1mZ2 |
3 E2m |
1 ImZ3. |
Полученная система уравнений содержит только токи ветвей свя зей, причем это – иначе записанные ЗНК. Правая часть содержит слагаемые с источниками ЭДС и тока, как в ЗНК, а в левой части записаны падения напряжения от токов ветвей связи:
Z11 1 Z1 2 Z2 – собственное сопротивление 1 го контура, т.е. сум ма сопротивлений ветвей, составляющих 1 й контур.
Обозначим:
Z31 1 Z13 1 Z2 – взаимное (общее) сопротивление цепи, т.е. общее сопротивление для 1 го и 3 го контуров.
Для k го контура с учетом введенных обозначений можно записать
1 |
1 |
1 |
1 |
(2.44) |
IkZkk |
1 InZnk |
2 IlZlk 23 2 4Ei |
3 4IiZi. |
|
Знаки у произведений вида 1 1n nk определяются по следующему
I Z
правилу: если в ветвях дерева направления обходов k го и n го кон туров – разные, то знак «–». При совпадении – знак »+».
Сравнивая полученный алгоритм (2.44) с выражением (1.27) при расчете цепей постоянного тока, нетрудно видеть их формальное сход ство. Как и при постоянном токе: количество уравнений по МТС в цепи гармонического тока Nмтс 1 p 2 q 31 2 n, где n – число идеальных источников тока, которые являются ветвями связей.
2.11. Анализ сложных цепей в гармоническом режиме методом узловых напряжений
При анализе цепей в соответствии с методом узловых напряже ний один из узлов выбирается за опорный и обозначают напряже ния остальных узлов относительно этого опорного узла. Число узловых напряжений, а, следовательно, и уравнений будет
Nмун 1 q 21.
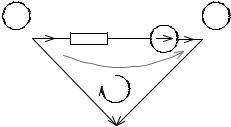
Покажем, что если известно напряжение на концах ветви, то все гда можно найти ток этой ветви (рис. 2.26).
46
|
|
3 |
|
5 |
3 |
112 |
4 |
|
612 |
212 |
|
|
|
3 |
|
|
|
712 |
|
|
3 |
3 |
|
|
711 |
721 |
|
1
Рис. 2.26
1
Напряжение ветви, напримерUkm , всегда можно выразить через уз ловыенапряжения.ИзЗНКдлябольшогоималенькогоконтуровимеем
1 |
1 |
1 |
3 0, |
Ukm |
1Umo |
2 Uko |
|
1 |
1 |
1 |
|
Ukm |
3 Uko |
2Um0. |
|
ПоЗНКдляконтура,содержащеговетвьссопротивлением(рис.2.26), получим
1 |
1 |
1 |
1 |
IkmZkm |
1Umo |
2Uko |
3 Ekm. |
Откуда ток ветви |
|
|
|
1 |
|
1 |
1 |
1 |
|
1 |
1 |
|
|
3 |
Uko |
1Umo |
2 Ekm |
3 |
Ukm |
2 Ekm |
|
||
Ikm |
|
|
|
|
|
|
. |
||
|
Zkm |
|
|
Zkm |
|||||
|
|
|
|
|
|
|
|||
Таким образом, ток ветви равен напряжению u, совпадающему по направлению с током, плюс значение источника ЭДС, если его на правление совпадает с направлением тока, деленному на сопротив ление ветви.
Метод узловых напряжений – это иначе записанные ЗТК, когда токи ветвей выражены через узловые напряжения, сгруппированы слагаемые при узловых напряжениях, а источники тока и токи пре образованных источников ЭДС, записаны в правой части уравнений.
При анализе цепей на основе МУН вначале выбирают опорный – ну левой узел. Если существует ветвь с идеальным источником ЭДС, то за опорный узел выбирают узел, принадлежащий данной ветви. При этом ток идеальной ветви определяется в последнюю очередь, исходя из ЗТК.
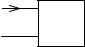
Запишем выражения для токов ветвей через узловые напряжения для цепи, изображенной на рис. 2.24. За опорный узел выбран ниж ний узел
47
1 |
|
1 |
|
1 |
1 |
|
1 |
1 |
1 |
|
1 |
1 |
|
|
U01 |
|
U10 |
|
U10 |
1 E1 |
|
U10 |
|||||
I1 |
2 |
|
2 1 |
|
, I2 |
2 |
|
|
, I3 |
2 |
|
|
3 Jm. |
Z1 |
Z1 |
Z2 |
|
Z3 |
|||||||||
|
|
|
|
|
|
|
|
|
|||||
Если ветвь имеет источник тока и его направление совпадает с
направлением тока ветви, то значение источника тока необходимо
1 1 2 1 2 1 3 0.
прибавить к току ветви, ЗТК для 1 го узла: I1 I2 I3 Подставляя выражения для токов через узловые напряжения и
группируя слагаемые, получим
1 |
1 |
|
1 |
|
1 |
|
1 |
1 |
|
|
|
|
E2 |
||||||
U10 |
( |
|
1 |
|
1 |
|
) 2 |
|
3 Jm. |
Z |
Z |
Z |
Z |
||||||
|
1 |
|
2 |
|
3 |
|
2 |
|
|
В общем случае для k го узла имеем следующий алгоритм состав ления уравнений методом узловых напряжений:
1 1 |
1 1 |
1 1 |
|
1 |
1 |
1 |
|
|
|
|
Ei |
|
|||||
UkoYkk |
1U1oYk1 |
1UmoYkm |
1 |
... 2 3J 1 |
3 |
|
2 3Jkk, |
(2.45) |
Z |
||||||||
|
|
|
|
|
|
i |
|
|
где Ykk – собственная проводимость k го узла, т. е. сумма проводимос тей ветвей, сходящихся к k му узлу; Ykm – общая проводимость вет
ви между k м и m м узлами; 1I11 – сумма токов источников тока и токов преобразованных источников ЭДС, причем знак у них »+», если они направлены к узлу k.
Сопоставляя полученный алгоритм (2.45) с правилом составления уравненийпоМУНдляпостоянноготока,видноихформальноесходство.
2.12. Мощность в цепи гармонического тока
3122 |
1 1122 |
Рис. 2.27
Рассмотрим двухполюсник, на входе которого гармонические напряжение и ток изменяются в со ответствии с выражениями (рис 2.27)
u(t) 1 Um sin2t, i(t) 1 Im sin(2t 3 4).
Найдем мгновенную мощность
p(t) 1 u(t)i(t) 1 ImUm sin2tsin(2t 3 4) 1 |
|
||
1 |
ImUm |
(cos4 5 cos(22t 3 4)). |
(2.46) |
|
|||
2 |
|
|
|
Как видно из выражения (2.46), мгновенное значение мощности
48
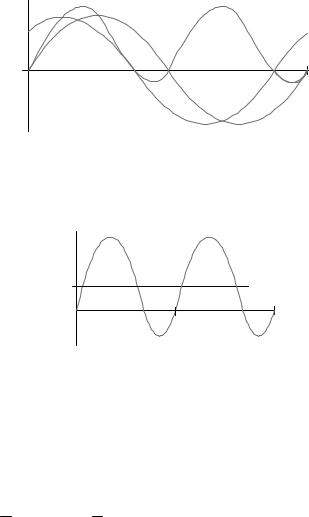
изменяется с удвоенной частотой по сравнению с током и напряже нием (рис. 2.28).
1122 |
2122 |
|
2 |
1122 |
|
Рис. 2.28 |
|
Рассмотрим отдельно кривую мгновенной мощности (рис. 2.29).
1112 |
|
|
|
2 |
|
2 |
|
|
|
|
|
2 |
2 |
2 |
|
1 |
|||
|
Рис. 2.29 |
|
|
Мгновенная мощность изменяется во времени. Пользоваться не удобно, поэтому вводят в рассмотрение среднее значение мощности за период изменения тока
|
|
T |
T |
|
P 1 |
1 |
6 p(t)dt 1 |
1 |
6IU(cos2 3 cos(24t 5 2))dt 1 |
T |
T |
|||
|
|
0 |
|
0 |
TT
1 1 6UIcos2dt 3 1 6IUcos(24t 5 2)dt 1 UIcos2 3 0 1 UI cos2.
T 0 T 0
Как видно, среднее значение мгновенной мощности Р не зависит от времени и оно носит название активной мощности. Итак, актив ная мощность определяется
49

T |
|
P 1 UIcos2 1 T1 3 p(t)dt, Вт. |
(2.47) |
0 |
|
Если угол = 0, то активная мощность Рмаксимальна и равна P=uI. |
|
Если угол = ± /2, то средняя мощность в цепи с индуктивностью либо |
|
емкостью равна нулю, т. е. индуктивность и емкость не потребляют |
|
энергию от источника за период тока (рис. 2.30). Вернемся к зависимо |
|
сти мгновенной мощности от времени. Там, где мгновенная мощность |
|
положительна, энергия от источника поступает в цепь и выделяется на |
|
активных сопротивлениях в виде тепла там, где отрицательна – энер |
|
гия, запасенная в магнитном поле индуктивности или в электрическом |
|
поле емкости, возвращается (рекуперируется) в источник. Таким обра |
|
зом, в цепи имеют место колебания мощности (энергии). При угле = |
|
90 активнаямощностьравнанулю,таккакзапервыйполупериодмгно |
|
венная мощность положительна, за второй – отрицательна (рис. 2.30). |
|
1112 |
|
1 |
|
t |
|
2 |
|
3 |
|
Рис. 2.30 |
|
Следовательно, индуктивность и емкость за период тока не по требляют активную мощность из источника.
МаксимальноезначениеактивноймощностиестьполнаямощностьS
S 1 UI, BA. |
(2.48) |
Полная мощность характеризует габариты всего устройства. По этому она часто называется габаритной, типовой мощностью.
Для характеристики реактивных элементов вводят понятие реак тивной мощности
Q 1 UIsin2, вар. |
(2.49) |
Найдем, как выражаются различные виды мощности на основе ме тода комплексных амплитуд, т.е. определим комплексную мощность. Пусть даны комплексы действующих значений напряжения и тока:
1 |
j u |
1 |
1 Ie |
j i |
. |
U 1 Ue |
|
, I |
|
50
