cudarikova2

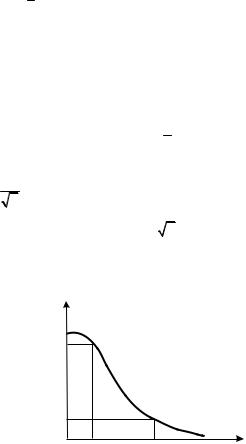
(рис. 3.11). Это максимальное значение выходного уровня качества называется предельным выходным качеством qL. Величина qL оз начает, что какова бы ни была доля дефектности в партиях до конт роля, выходной уровень качества продукции будет в среднем не более qL. Если, например, используется план выборочного контроля, для которого предельное выходное качество qL = 0,01, то это означает, что в среднем засоренность принятой продукции будет не более 1 %.

Пусть для контроля качества используется план с приемочным числом c = 0, а закон распределения числа дефектных изделий в вы борке может быть аппроксимирован распределением Пуассона. Тог да в соответствии с (3.29)

Дифференцируя полученное выражение по q и приравнивая про изводную нулю, найдем значение q, при котором qвых обращается в максимум. Подставив это значение в (3.30), получим

В случае произвольного с предельный выходной уровень качества может быть вычислен по формуле

где функция ρc берется из табл. 3.6 [5].

Важной характеристикой планов контроля с разбраковкой явля ется средний объем инспекции, вычисляемый как математическое ожидание числа подвергнутых контролю изделий. Заметим, что объем инспекции равен объему выборки, если партия принимается [с веро

q вых (q)

Рис. 3.11. Зависимость уровня среднего выходного качества от доли де% фектных изделий в партии

51

Таблица 3.6. Зависимость значения функции ρc от приемочного числа c

ятностью L(q)], и объему партии, если она бракуется [с вероятнос тью 1–L(q)]. Следовательно, средний объем инспекции

Впрактике проведения контроля качества с разбраковкой распро странены два принципа планирования контрольных испытаний: по среднему и предельному качеству.

Рассмотрим принцип планирования по величине qL.

Вработе [1] показано, что при заданном значении с в случае рас пределения Пуассона объем испытаний n с учетом предельного вы ходного уровня качества может быть определен по формуле

где KM = qL/qн; Θ = Nqн, qн — средняя доля дефектных изделий в партии при нормальном ходе производства.

Из всех возможных значений n, удовлетворяющих уравнению (3.34) (при различных c), отбирается такое значение, которое мини мизирует средний объем инспекции (3.33).

Для этого в табл. 3.7 [5] для значений KM приведены критические значения параметра Θc. Если при заданном KM оказывается, что Θ≤Θc, то приемочное число полагают равным нулю; если Θ −1 ≤ Θ < Θ , то приемочное число c = 1.

Расчет оперативной характеристики такого плана контроля про изводится по уравнению (3.4) с учетом (3.9).

Пример 3. Задано qL = 0,01. Известно, что нормальное производство обеспечивает уровень качества qн = 0,005, т. е. KM = 2. Объем партии — 1000 изделий. Определить объем выборки и приемочное число.

52

Таблица 3.7. Критические значения параметра Θc для различных значений KM

KM

53

Решение. Из табл. 3.7 для KM = 2 находим, что Θ0 = 1,676 и Θ1 = 6,723. В примере Θ = Nqн = 1000×0,005 = 5, и, следовательно, надо принять c = 1. По табл. 3.6 определяем ρc = 0,840, и из уравнения (3.34) находим n = 77.

Таким образом, план (n = 77, c = 1) обеспечивает наиболее экономич ный, с точки зрения изготовителя, план контроля.

3.7. Статистический приемочный контроль по количественному признаку

3.7.1. Постановка задачи

Контроль по количественному признаку обладает более высокой информативностью, чем контроль по альтернативному признаку. Дело в том, что при анализе количественного признака у каждого изделия выборки измеряется параметр, и каждая выборка дает ин формацию, состоящую из n (объем выборки) чисел. При альтерна тивном контроле объем информации состоит только из количества дефектных изделий в выборке. Поэтому количественный контроль при той же достоверности выводов требует меньшего объема выбо рок.

Рассмотрим случай, когда количественный признак изделия име ет нормальное распределение с параметрами μ и σ:

Качество продукции, т. е. вероятность изготовления дефектного изделия q, как это видно из рис. 3.12, полностью определяется тех ническим допуском на контрольный признак (Tн, Tв) и соотношени

Рис. 3.12. Вероятности изготовления дефектной продукции q1 и при нор% мальном распределении признака качества

54

ем между генеральным математическим ожиданием μи средним квад ратическим отклонением σ.

Задача выборочного контроля по количественному признаку за ключается в том, чтобы по результатам анализа выборочных харак теристик:

среднего арифметического выборки

выборочного среднего квадратического отклонения

n

s = 1 ∑(xi −x)2, (3.37) n −1 i=1

– делатьутверждениеотносительногенеральныххарактеристикμиσ.

3.7.2. Контроль по одному количественному признаку при одностороннем допуске и известной дисперсии

Контроль по количественному признаку достаточно сложен как в организационном, так и математическом отношении. Поэтому рас смотрим лишь наиболее простые случаи количественного контроля, когда признак X имеет нормальное распределение (с известной и не известной дисперсией σ2) и односторонний допуск.

Пусть изделие считается годным, если контрольный признак X≤T. В противном случае изделие классифицируется как дефектное. Тогда уровень качества q может быть найден по уравнению

где Φ(X) – табличная функция (табл. 3.8) [5].

Предположим, что разладки технологического процесса приводят только к смещению центра рассеяния контрольного признака μ, а точность технологического процесса σ2 остается неизменной. Тогда дисперсию случайной величины можно рассматривать как постоян ный параметр, который всегда может быть заранее определен путем проведения специального эксперимента.

Из (3.38) видно, что при сформулированных условиях вариации качества полностью определяются вариациями генерального мате матического ожидания μ.

55

Таким образом, требование к качеству партий q ≤q0 эквивалентно требованию μ≤μо, где μо – значение математического ожидания, оп ределяемое из уравнения

Аналогично требование q ≥qm эквивалентно требованию μ≥μm, где μm определяется из уравнения

Поскольку μ x, то для сформулированного правила классифи кации изделий на годные и дефектные условие приемки партии запи сывается в виде

Запишем уравнение оперативной характеристики:

Учитывая, что случайная величина x имеет нормальное распре деление с математическим ожиданием μи средним квадратическим

отклонением σ , где n – объем выборки, окончательно имеем

График оперативной характеристики показан на рис. 3.13.

L( )

1,0

1–

0m

Рис. 3.13. График оперативной характеристики плана контроля по ко% личественному признаку

57

Если требования к плану контроля сформулированы в виде q0, qm, α, β, то имеют место следующие уравнения:

где μ0 и μm определяются из уравнений (3.39), (3.40).

Переходя от уравнений (3.44) и (3.45) к квантилям нормального распределения и учитывая, что μ0 ≤c ≤μm, получим

Эта система уравнений является основой для выбора параметров плана контроля n и c.

После суммирования уравнений (3.46) и (3.47) и простых преоб разований имеем уравнение для определения объема выборки

σ

Результаты расчетов по уравнению (3.48) сведены в табл. 3.9 [5]. В ряде случаев для оперативной оценки объема выборки может

оказаться полезной зависимость

полученная путем несложных алгебраических преобразований урав нений (3.39), (3.40), (3.44) и (3.45), представленных в квантильной форме.

Уравнение (3.49) справедливо также для случая, когда техничес кий допуск установлен так, что изделие считается годным, если X ≥T, и дефектным, если X < T. В уравнении (3.48) в этом случае знамена

тель должен быть записан следующим образом: μ0 −σμm .

58

Таблица 3.9. Результаты расчетов объема выборки по уравнению (3.48)

Таблица 3.10. Квантили нормального распределения

59

Для оценки эффективности планов контроля по количественному признаку и сравнения с аналогичными планами по альтернативному признаку рассмотрим пример.

Пример. Заданы: q0 = 0,01; qm = 0,05; α= β= 0,1. Допуск односто ронний. По табл. 3.10 квантилей нормального распределения [5, 6] находим значения квантилей, соответствующих вероятностям 1–q0,

1–qm, 1 – α, 1 – β. Имеем: u1−q0 = 1,645; u1–α = = 1,282. Подставив полученные значения в (3.48), получим

n = 7. Для тех же условий соответствующий план одноступенчатого контроля: n= 105, c= 2. Таким образом, в данном примере контроль по количественному признаку дает сокращение объема выборки в 15 раз.

3.7.3. Контроль по одному количественному признаку при одностороннем допуске и неизвестной дисперсии

Рассмотрим случай, когда разладки технологического процесса приводят не только к смещению центра рассеяния μ, но и к измене нию точности процесса σ2. В этом случае дисперсию контрольного признака σ2 следует считать неизвестной и в процессе испытаний кон тролировать оба параметра. Пусть так же, как и в предыдущем слу чае, для параметра X установлен допуск: при X ≤T изделие считается годным, в противном случае – дефектным.

Для вычисления вероятности q справедливо уравнение (3.38), из которого следует, что качество продукции определяется не только математическим ожиданием генеральной совокупности m, но и гене ральной дисперсией σ2. Из уравнения (3.38) можно записать выра жение, устанавливающее соотношение между μи σ, которое обеспе чивает выпуск продукции с уровнем качества q:

Зависимость (3.50) называется уравнением изодефектной линии. Для сформулированных правил классификации изделий графики изодефектных линий представлены на рис. 3.14, причем с увеличе

нием q наклон прямой увеличивается.

Для заданных q0, qm можно записать следующие два уравнения изодефектных линий:

60