cudarikova2

ка первого рода). С другой стороны, при засоренности партии дефек тными изделиями в выборке может оказаться сравнительно неболь шое количество дефектных, и плохая партия будет принята (ошибка второго рода).

Задача заключается в том, чтобы в условиях выборочного контро ля такие ошибочные заключения делались крайне редко, а степень их возможности была заранее определена. Ошибки первого и второго рода должны учитываться при планировании приемочного контро ля, а также контрольных испытаний.

Для оценки эффективности плана выборочного контроля служит так называемая оперативная характеристика, или, как ее иначе называют, рабочая характеристика. Под оперативной характери стикой плана контроля понимают функцию P(q), равную вероятнос ти принятия партии с уровнем качества q.

Рассмотрим оперативную характеристику плана сплошного кон троля.

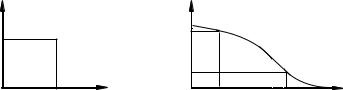
В процессе контроля каждого образца в партии оказывается точно известным количество дефектных образцов в партии. Если это коли чество больше некоторого критического значения Mкр = Nqкр (N – объем партии), то такая партия обязательно (с вероятностью, рав ной единице) будет отклонена как не соответствующая требованиям потребителя. Если количество дефектных образцов в выборке мень ше Mкр, то партия с вероятностью единица будет принята. При этом считают, что ошибки, связанные с определением степени пригоднос ти образца, исключены. Оперативная характеристика плана сплош ного контроля показана на рис. 3.2, а. Такую оперативную характе ристику будем называть идеальной. Однако построить выборочный план с такой рабочей характеристикой невозможно. В этих случаях поставщик и потребитель договариваются о двух уровнях качества q0 и qm: партии с уровнем качества q ≤ q0 считаются заведомо хороши ми, а партии с уровнем качества q ≥ qm, причем qm > q0, – плохими. Интервал q0 ≤ q ≤ qm считается зоной неопределенности. Партии с таким уровнем качества считаются еще допустимыми. Величина q0

называется приемочным уровнем качества, величина qm – брако вочным уровнем качества.

Таким образом, вся продукция делится на три категории: продукция первой категории, уровень качества которой q ≤ q0; продукция второй категории, уровень качества которой q ≥ qm; продукция третьей категории, уровень качества которой удов

летворяет соотношению q0 < q < qm.

К плану контроля предъявляются требования, состоящие в том, что партии первой категории должны по возможности приниматься,

31

Рис. 3.2. Оперативные характеристики плана контроля: а – сплошного; б – статистического

второй – по возможности браковаться. В количественном отноше нии эти требования выражаются в том, что вероятность принятия партии с уровнем качества q ≤q0 должна быть меньше величины 1 – α, а вероятность приемки партий, у которых q ≥ qm, не должна превы шать величины β.

Величины α и β называют соответственно риском поставщика и риском потребителя и представляют собой вероятности ошибок пер вого и второго родов. Риск поставщика a есть вероятность приня тия ложного решения о браковке хорошей партии (поставщик рис кует понести неоправданные убытки). Риск потребителя βесть ве роятность принятия ложного решения о принятии плохой партии (понести убытки рискует потребитель).

Задание рисков αи βобеспечивает гарантии поставщика и потре бителя в отношении забракования хороших и приемки плохих партий. На практике величины αи βвыбираются равными 0,1; 0,01; 0,05. Назначение их не является статистической задачей, а полнос тью определяется последствиями от неверно принятых решений (оши бок первого и второго рода).

Таким образом, если требования поставщика и потребителя сфор мулированы в виде четырех чисел, например: q0 = 0,01; qm = 0,05; α = β = 0,1, – то это значит, что в среднем из каждых ста партий, имеющих уровень дефектности не более 1 %, будет забраковано не более пяти партий, а из 100 партий, содержащих 5 и более дефект ных изделий, будет принято не больше пяти партий.

Таким образом, для любого плана приемочного контроля спра ведливы уравнения

Учитывая также, что P(0) = 1,P(1) = 0, легко представить вид опера тивной характеристики статистического плана контроля (рис. 3.2, б).

32

Уравнения (3.1), (3.2) являются основой для задания плана при емочного контроля, т. е. назначения объема выборки и нормативов, с которыми сравниваются результаты контроля, и вычисления опе ративной характеристики P(q).

Рассмотрим, как назначаются требования q0 и qm.

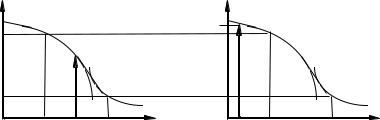
Величина браковочного уровня качества (qm) выбирается исходя из требований потребителя, которому необходима продукция с уров нем качества не ниже qm. Величина приемочного уровня качества (q0) устанавливается с учетом возможностей производства, которое дол жно обеспечить выпуск продукции с уровнем качества qн ≤q0, где qн – средний уровень засоренности партий при нормальном ходе произ водства. Только в этом случае поставщик гарантирует себя от на прасной браковки хороших партий, выпущенных при соблюдении основных требований технологии. Как правило, значение q0 немного больше qн. В противном случае эффективность плана контроля сни жается. Действительно, если приемочный уровень качества много меньше qн, вероятность принятия партий, как это видно из рис. 3.3, резко падает, и действительный риск поставщика αд увеличивается. При выборе q0, значительно превышающего qн, действительный риск поставщика меньше a, однако такой план контроля окажется, как это будет видно из дальнейшего, фактически неэффективным, так как потребует больших объемов выборок.

Таким образом, знание: 1) требований потребителя к качеству про дукции, 2) уровня, достигнутого предприятием изготовителем, 3) последствий от принятия ложных решений о приемке и браковке партий, – оказывается необходимым и достаточным для планирова ния контрольных испытаний по принципу недопустимого в эксплуа тации уровня качества. Предварительная оценка эффективности плана контроля производится с помощью оперативной характерис

1д

Рис. 3.3. Действительный риск поставщика при необоснованном зада% нии приемочного уровня качества

33

тики, характер правой части которой должен удовлетворять требо ваниям потребителя, левой – требованиям поставщика, а средней – того или другого в зависимости от степени ответственности контро лируемых изделий. Более полная оценка эффективности может осу ществляться с учетом статистической оценки уровня качества при нятой продукции. Такие оценки в статистическом приемочном конт роле называются последующими.

3.5. Общий алгоритм статистического приемочного контроля партий продукции

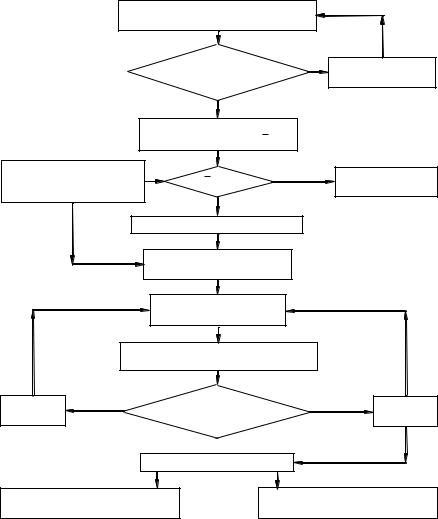
Общий алгоритм приемочного контроля показан на рис. 3.4.

1.Партия, предъявляемая для контроля, представляет собой совокупность единиц продукции одного наименования, типоразмера

иисполнения, произведенную в течение определенного интервала времени в одних и тех же условиях. На контроль могут поступать как отдельные партии, так и последовательность партий. Объем контролируемой партии N устанавливают исходя из условий произ водства (например, равным сменному заданию). Допускается коле бание объемов контролируемых партий в пределах, указанных в со ответствующем стандарте на статистический приемочный контроль. Например, ГОСТ 18242–72 (СТ СЭВ 548–77, СТ СЭВ 1673–79), ГОСТ 20736–75 (СТ СЭВ 1672–79) допускают колебание объема партии в пределах 91–150, 151–280, 281–500 и т. д. единиц продук ции. При соблюдении указанных пределов колебание объема партии не влияет на план контроля.

Контролируемую партию следует отличать от поставляемой по требителю или приобретаемой потребителем; последние могут быть сформированы как из части годной контролируемой партии, так и из одной или нескольких годных контролируемых партий.

2.Приемочный уровень дефектности q0 устанавливают по со глашению между поставщиком и потребителем продукции исходя из технико экономических соображений. Понятия «поставщик» и «по требитель» достаточно условны; в общем случае под поставщиком следует понимать сторону, предъявляющую продукцию на контроль, а под потребителем – сторону, использующую данную продукцию и заинтересованную в результатах контроля. Например, поставщиком может быть механический цех (участок), а потребителем – сбороч ный цех (участок) и т. п. Потребитель заинтересован в поставке без дефектной продукции, поэтому для него предпочтительно значение

q0 = 0, но тогда статистические методы неприменимы. В то же время стандартизованные планы статистического контроля содержат дос

34

0

?@545;8BL A@54=89 2E>4=>9 C@>25=L 45D5:B=>AB8q

Рис. 3.4. Общий алгоритм приемочного контроля (* – при многоступен% чатом контроле – для каждой ступени)

таточно широкий диапазон q0, поэтому во многих случаях может быть достигнут технически и экономически обоснованный компромисс между требованиями потребителя и реальными возможностями по ставщика.

3. После того, как величина q0 установлена, необходимо опреде лить реальный уровень дефектности контролируемой продукции

35

по результатам сплошного или выборочного контроля нескольких партий. Средний входной уровень дефектности q определяют как средний процент дефектных единиц или среднее число дефектов на 100 единиц продукции. Второе соотношение используют в случаях, когда в единице продукции может быть более одного дефекта и важно знать общее число дефектов. Если q > q0, то возрастает число забра кованных партий, а поскольку такие партии обычно подвергают сплошному контролю, то общая трудоемкость контроля значитель но увеличивается и статистический контроль становится нецелесо образным.

4.Далее выбирается уровень контроля. Уровни контроля пре дусмотрены ГОСТ 18242 и ГОСТ 20736. При переходе с более высо кого уровня на более низкий уменьшается относительный объем вы борки и увеличивается риск поставщика и особенно риск потребите ля. Уровни контроля бывают общими (в стандартах их три) и специ альными. Основным для применения является II общий уровень. Специальные уровни контроля позволяют существенно уменьшить объем выборки, что бывает необходимо, например, при разрушаю щем контроле дорогостоящих изделий. Обоснованный выбор уровня контроля может быть сделан лишь на основе сопоставления опера тивных характеристик планов контроля на разных уровнях, по ко торым определяют риски поставщика и потребителя.

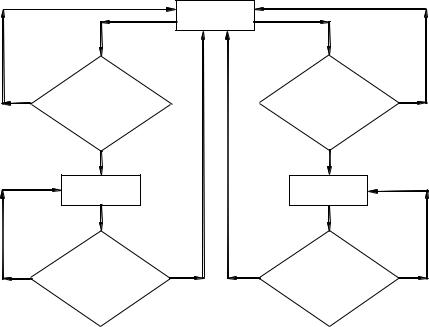
5.Указанные стандарты предусматривают также три вида конт роля: нормальный, усиленный и ослабленный. Обычно начинают с нормального контроля, переходя к усиленному или ослабленному в зависимости от результатов приемки последовательности партий (рис. 3.5). Такой переход называется корректировкой плана конт роля.

6.После выполнения рассмотренных действий устанавливают по таблицам соответствующего стандарта объем выборки и конт рольный норматив. Порядок пользования стандартами на стати стический приемочный контроль детально изложен как в самих стан дартах, так и в методических указаниях РД 50 605–86, а потому здесь не описывается.

7.Эффективность выбранного плана контроля оценивают с помо щью его оперативной характеристики, представляющей собой зависимость вероятности P(q) приемки партии от уровня дефектно сти q в этой партии при данном плане контроля. Наиболее наглядна эта зависимость в графической форме, поэтому следует построить гра фик оперативной характеристики по данным, приведенным в стан

дартах (в ГОСТ 20736 приведены готовые графики). По графику мож но определить риск поставщика α = 1–P(q0) – вероятность забрако

36

>@<0;L=K9 :> =B@>;L

Рис. 3.5. Алгоритм корректировки планов контроля

вания «хорошей» партии и риск потребителя β= P(qm) – вероятность приемки «плохой» партии (с браковочным уровнем дефектности qm) или же определить, какая величина браковочного уровня соответ ствует заданному риску потребителя β.

Построенная оперативная характеристика отражает лишь стати стическую недостоверность результатов контроля выборки; при этом предполагается, что каждая единица продукции в выборке контро лируется безошибочно. На самом деле контроль единиц в выборке сопровождается погрешностями измерений, вследствие чего возни кает дополнительная недостоверность.

Реальная оперативная характеристика Pδ(q) при наличии по грешности измерения δопределяется формулой

Pδ(q) = P(q + q),

где q – величина сдвига, зависящая от величины q и относительной погрешности контроля (определяется по таблице).

Сдвиг оперативной характеристики приводит к увеличению рис ка поставщика a при фиксированном q0 и уменьшении qm при фикси рованном риске потребителя β, что должно быть учтено при выборе

37

плана контроля и средства измерений (средства контроля). При от носительной погрешности контроля менее 10–15 % влиянием по грешности измерений можно пренебречь.

3.6. Статистический приемочный контроль по альтернативному признаку

3.6.1. Одноступенчатый приемочный контроль

Пусть на контроль предъявлена партия объемом N, содержащая M дефектных изделий. Из партии случайным образом отбирается выборка объемом n штук. Партия принимается, если в выборке ока жется не более c дефектных изделий, в противном случае партия бра куется. Такая система правил оценки качества товарной партии и составляет сущность одноступенчатого приемочного контроля. Схема изложенной процедуры контроля представлена на рис. 3.6.

Рассмотрим оперативную характеристику плана одноступен чатого приемочного контроля.

При сформулированных условиях число дефектных изделий в выборке имеет гипергеометрическое распределение, поэтому вероят ность того, что в выборке окажется ровно т дефектных образцов, равна

N

где Chk – число сочетаний из h элементов по k.

Поскольку в выборке допускается не более с дефектных изделий, вероятность приемки партии (оперативная характеристика) опреде ляется как сумма вероятностей попадания в выборку 0, 1, 2, …, c бракованных изделий:

m=0

B

@0:>2:0

c+1 c

@85<: 0

Рис. 3.6. Процедура одноступенчатого приемочного контроля

38

Уравнения (3.3) и (3.4) определяют основные свойства оператив ной характеристики, а именно:

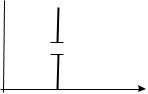
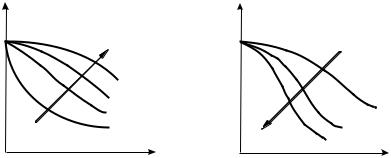
1)при фиксированном объеме выборки с ростом приемочного чис ла c вероятность приемки партии увеличивается (рис. 3.7, а);

2)при фиксированном приемочном числе c с ростом объема выбор ки вероятность приемки партии уменьшается (рис. 3.7, б).

Отсюда вытекает очень важное в практическом отношении след ствие: часто применяемые в производстве планы контроля с объемом выборки, составляющим определенный процент от объема партии, в условиях переменного N и постоянного c могут оказаться малоэф фективными, так как с изменением выборки меняется также и веро ятность приемки партии.

Выбор плана одноступенчатого контроля заключается в назна

чении объема выборки n и приемочного числа c. Если требования к плану контроля сформулированы в виде задания q0, qm, αи β, – объем выборки и приемочное число могут быть найдены как корни систе мы (3.1) и (3.2), которая в данном случае запишется следующим об разом:

n

Рис. 3.7. Изменение вероятности приемки партии при постоянных: а – объеме выборки и различных значениях приемочного числа c; б – приемочном числе c и различных значениях объема выборки

39

Вычисление величины Pm затруднительно. Но известно, что при N →∞гипергеометрическое распределение приближается к биноми альному, особенностью которого является независимость его от объе ма партии. На практике, если n ≤0,1N, вместо гипергеометрического распределения можно использовать биномиальное.

В этом случае вероятность попадания в выборку m дефектных из делий вычисляется по формуле

а вероятность приемки партии

m=0

Дальнейшее упрощение вычислений связано с заменой биноми ального распределения распределением Пуассона, которое с доста точной точностью можно применять, когда доля дефектных изделий в партии не превосходит 0,1. В этом случае можно пользоваться фор мулой

На практике распространен случай одноступенчатого контроля с приемочным числом c, равным нулю. Оперативная характеристика этого плана контроля для случая, когда число дефектных изделий в выборке имеет биномиальное распределение, вычисляется по формуле

При заданных qm и β данный план обеспечивает минимальный объем контроля.

Для рисков поставщика и потребителя можно записать уравне ния:

из которого следует, что обеспечить заданные риски αи βпри плане контроля с c = 0 можно только при определенном соотношении q0 и qm, не зависящем от объема выборки n.

40