cudarikova2

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

САНКТ ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ

Е. В. Сударикова

НЕРАЗРУШАЮЩИЙ КОНТРОЛЬ В ПРОИЗВОДСТВЕ

Часть 2

Учебное пособие

Санкт Петербург 2007

УДК 620.17(075) ББК 30.607я7

С89

Рецензенты:

кафедра измерительных технологий и компьютерной томографии Государственного университета ИТМО;

кандидат технических наук, доцент О. Б. Шалагинова

Утверждено редакционно издательским советов университета в качестве учебного пособия

Сударикова Е. В.

С89 Неразрушающий контроль в производстве: учеб. пособие.

Ч.2.; ГУАП. — СПб., 2007. — 112 с.: ил. ISBN 5 8088 0232 6 (Ч. 2)

Изложены основные понятия и общие положения статистическо го контроля качества продукции: методы формирования партий и выборок промышленной продукции для контроля ее качества, опре деление объема выборок, план контроля, его характеристики и прин ципы его выбора. Рассмотрены основы статистических методов уп равления качеством и организация подразделений неразрушающе го контроля на базе теории массового обслуживания.

Предназначено для студентов, обучающихся по специальности 200102 «Приборы и методы контроля качества и диагностики».

УДК 620.17(075) ББК 30.607я7

Учебное издание

Сударикова Елена Васильевна

НЕРАЗРУШАЮЩИЙ КОНТРОЛЬ В ПРОИЗВОДСТВЕ

Часть 2

Учебное пособие

Редактор В. П. Зуева Верстальщик Т. М. Каргапольцева

Сдано в набор 26.02.07. Подписано к печати 21.03.07. Формат 60х84 1/16. Бумага офсетная. Печать офсетная. Усл. печ. л. 7,1.

Уч. изд. л. 8,1. Тираж 100 экз. Заказ №

Редакционно издательский центр ГУАП 190000, Санкт Петербург, Б. Морская ул., 67

2

3

4

3. ОСНОВЫ СТАТИСТИЧЕСКИХ МЕТОДОВ УПРАВЛЕНИЯ КАЧЕСТВОМ

3.1.Применение теории вероятности

квопросам контроля качества

Технологический процесс изготовления изделий содержит более или менее значительные ошибки случайного характера, т.е. возни кающие в результате влияния непостоянно действующих факто ров. К ним относятся, например, отклонения размеров деталей одно го типоразмера в полях допусков на параметры. При последующей сборке таких деталей в результате случайного неблагоприятного со четания отклонений параметров, лежащих в полях своих допусков, может произойти весьма существенное ухудшение качества изготав ливаемого изделия. Такие ошибки следует отличать от системати ческих, которые возникают в результате неправильного выбора ма% териалов, конструкции, неверных технологических предписаний.

К систематическим ошибкам технологического процесса относятся, например, ошибка в расчете шихты для последующей плавки метал ла, а также неправильный выбор режима нагрева и охлаждения спла ва при термообработке, в результате чего его структура и свойства не соответствуют заданным. Процесс контроля изделий также содер жит ошибки случайного характера. Например, при ручном контро ле уставший контролер может не заметить дефект и отнести брак к годным изделиям.

Для изучения случайных процессов привлекают методы статис тики. Статистический контроль базируется на теории вероятностей. Применительно к вопросам контроля качества продукции основные понятия теории вероятности интерпретируются следующим образом.

Генеральная совокупность – большая партия однотипной про дукции, все количество однотипных изделий, выпускаемых одним или даже несколькими предприятиями.

Выборка – некоторое количество изделий, выпущенных за опреде ленный период времени или отобранных для выборочного контроля.

Закон распределения вероятности – зависимость между значе ниями измеряемых случайных величин и вероятностью их появле ния.

Понятие вероятности применимо к дискретным и непрерывно ме няющимся величинам.

5

Вероятность дискретных величин

Дискретной величиной является, например, вероятность нахож дения числа дефектных и годных изделий в выборке из изделий, взя тых для испытания (контроля).

Если вероятность наблюдения брака в результате одного испыта ния равна p, то вероятность обнаружить k бракованных изделий в выборке объемом n будет

Этот закон распределения вероятностей называется биномиаль ным.

Математическое ожидание (среднее значение) для биномиального законараспределенияслучайнойвеличиныопределяетсявыражением

n

p = n−1 ∑kp(k) = np.

k=1

Это довольно очевидный результат: если вероятность брака p, то в выборке из n изделий наиболее вероятно встретим np бракованных изделий.

Дисперсия показывает, насколько велик разброс значений слу чайной величины относительно найденного среднего значения. Для биномиального распределения она равна

n

D = 1 ∑[p(k) − p]2 p(k) = np(1− p). n −1 k=1

Среднее квадратическое отклонение

σ = D = np(1− p).

Кумулятивная (накопленная) вероятность – вероятность того, что брак встречается в выборке не более чем m раз

m

P(m) = ∑ p(k).

k=1

При m = n имеем P(m) = 1, так как сумма всех вероятностей (досто верного события) равна 1.

Если в действительности испытать выборку из п изделий на коли чество годных n–k1 и бракованных k1, то найденные k1/n и (n–k1)/n

6

(их называют частостями событий) будут отличаться от p(k), p(n–k). Однако многократное повторение таких испытаний приведет к тому, что средние значения частостей будут приближаться к веро ятностям и сравняются с ними при бесконечно большом повторении испытаний.

Вероятность непрерывных величин

Примером распределения непрерывной величины может служить очень часто встречающееся в технике нормальное или гауссовское распределение.

Плотность распределения вероятности гауссовского распределе ния

показывает вероятность того, что изучаемая величина лежит в бесконечно узком интервале от x до x + dx.

Среднее значение случайной величины есть

∞

x = ∫ xf(x)dx.

−∞

Дисперсия

∞

D = ∫ (x −x)2 f(x)dx = σ2.

−∞

Интегральный закон распределения непрерывной случайной ве личины

x

F(x) = ∫ f(x)dx

−∞

есть вероятность того, что измеряемая величина не превосходит не которое заданное значение x. Эта вероятность аналогична кумуля тивной вероятности. Если исследуемая величина (например, проч ность) не имеет отрицательных значений, то нижний предел интег рирования будет равен 0.

Нормальное распределение (рис. 3.1) характеризует разброс отно сительно среднего значения механических свойств материалов (проч ности, упругости), результатов различных измерений (измерения

7

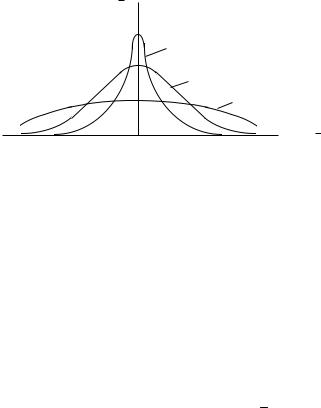
P (x x )

= 0,5

1

2

x x

Рис. 3.1. Нормальный закон распределения (на кривых указано среднее квадратическое отклонение)

размеров дефектов). На примере этого распределения особенно хоро шо видно, что чем больше σ, тем более широкой является кривая распределения относительно среднего значения.

При этом полная площадь под кривыми распределения остается равной единице (F(∞)=1). Если пределы интегрирования ограничить конечным значением x = x0, то F(x0) < 1. Если принять x0 = x ± 3σ, то вероятность будет равна 0,9973. Это означает, что практически все возможные значения случайных событий лежат в интервале x ±3σ . В интервале x ±2σ содержится приблизительно 95 % вероятностей случайных событий.

Существует строгое доказательство (теорема Лапласа), что при большом n биномиальное распределение с хорошим приближением (тем точнее, чем больше n) может быть описано с помощью нормаль ного распределения с теми же средним значением и дисперсией, что у биномиального. Из этого следует, что интервал x ±3σ охватывает практически все возможные значения случайных величин не только для нормального, но также для биномиального распределения.

3.2. Статистический контроль качества продукции. Основные понятия. Общие положения

3.2.1. Задачи и условия статистического контроля

Введение контроля всегда увеличивает издержки производства за счет появления дополнительных непроизводственных расходов, ко торые приводят к удорожанию продукции. Однако при правильно организованном контроле снижаются расходы на изготовление и эк сплуатацию некачественной продукции.

С применением статистических методов решают следующие ос новные задачи контроля:

8

1)статистический анализ результатов контроля с целью регули рования технологии производства;

2)статистический, т. е. выборочный, контроль; при этом уста навливаются оптимальные планы выборочного контроля и крите рии оценки его результатов (в соответствии с задачами производства

иэксплуатации изделий);

3)оценка точности и достоверности результатов контроля, опти мизация методики контроля;

4)установление корреляционных связей между показателями качества, технологией изготовления продукции и ее эксплуатацион ными характеристиками; установление критериев оценки качества с учетом названных факторов, т. е. норм допустимых дефектов.

Необходимым условием применения статистических методов кон троля является отлаженность и стабильность технологического про цесса. Процесс считается отлаженным, если полностью выявлены

иустранены нарушения технологической дисциплины, и стабиль ным, если распределение вероятностей его параметров остается по стоянным в течение некоторого интервала времени без вмешатель ства извне. Для применения статистического регулирования необхо димы еще два условия:

1)выявлены систематические погрешности как причины возмож ных разладок (например, смещение настройки) и способы корректи рования значений параметров технологического процесса для их опе ративного устранения;

2)коэффициент точности по контролируемому параметру (ГОСТ 27.202–83) удовлетворяет условию

KT = ω ≤ 1,

T

где ω– поле рассеивания или разность максимального и минималь ного значений контролируемого параметра за установленный проме жуток времени (наработку технологической системы); T – допуск на контролируемый параметр.

Отлаженный и стабильный процесс, удовлетворяющий этим ус ловиям, считается статистически управляемым.

Проверку указанных условий выполняют путем предварительно го анализа точности и стабильности технологического процесса в со ответствии с ГОСТ 27.202–83. На этапе подготовки производства для анализа используют главным образом расчетные методы, а на этапе изготовления продукции – опытно статистические методы. Для применения стандартизованных планов контроля по количествен ному признаку необходимо также в процессе предварительного ана

9

лиза проверить нормальность распределения контролируемого пара метра по СТ СЭВ 1190–78.

Применение статистического контроля взамен сплошного там, где это возможно, позволяет снизить трудоемкость и стоимость контроля, высвободить часть контрольного персонала. Вместе с тем, статистичес кий контроль предъявляет повышенные требования к квалификации разработчиков и исполнителей контроля, а также к точности средств измерений. Поэтому окончательный выбор вида контроля следует про изводить на основании комплексного экономического критерия.

Статистический контроль осуществляют в следующих вариантах:

1)статистический приемочный контроль партий продукции;

2)непрерывный статистический приемочный контроль;

3)статистическое регулирование технологического процесса.

3.2.2. Основные понятия

Основная терминология статистического контроля приведена в соответствии с ГОСТ 15895–77.

Поток продукции – продукция одного наименования, типоно минала или типоразмера и исполнения, находящаяся в движении на технологической линии.

Контролируемая партия продукции – это одновременно пред ставленная для контроля совокупность единиц продукции одного наименования, типономинала или типоразмера и исполнения, про изведенная в течение определенного интервала времени в одних и тех же условиях.

Вобщем случае могут рассматриваться два типа совокупностей, связанных с понятием партии: совокупность конечного объема ре альных объектов и совокупность бесконечного объема реальных или гипотетических объектов. При контроле качества обычно исходят из того, что задана совокупность конечного объема, а при контроле на дежности предполагают, что генеральная совокупность имеет беско нечный объем.

Объем партии – число единиц продукции, составляющих партию. Выборка – изделие или определенная совокупность изделий, ото

бранных для контроля из партии или потока продукции.

Взависимости от степени завершенности продукции к изделиям допускается относить завершенные и незавершенные предметы про изводства, в том числе заготовки.

Мгновенная выборка – выборка из потока продукции, которую составляют изделия, произведенные последними к моменту отбора в течение достаточно короткого интервала времени.

10