
Курс лекций
.pdf
Необходимо сделать двухступенчатый Т – триггер в базисе Шеффера и в базисе Пирса.
Базис Шеффера :
 - Обозначение по ближнему фронту.
- Обозначение по ближнему фронту.
Базис Пирса :
- Обозначение по дальнему фронту.
§1.4.7. JK – триггер (универсальный)
JK-триггер характеризуется таблицей:
|
|
|
|
|
|
|
|
|
|
J(t) |
K(t) |
Q(t+1) |
Q(t+1) = K(t)Q(t) V J(t)Q(t) |
||||||
|
|
|
|
|
|
|
|
|
|
0 |
0 |
Q(t) |
|
|
|
|
|
|
|
S(t) = J(t)Q(t) |
|||||||||
0 |
1 |
0 |
|||||||
|
|
|
|
|
|
||||
1 |
0 |
1 |
R(t) = K(t)Q(t) |
||||||
1 |
1 |
Q(t) |
|
|
|
|
|
|
|
Он отличается от RS-триггера тем, что при поступлении на входы комбинации J=K=1 меняет состояние выхода на противоположное.
Q(t+1)= Q(t). Таким образом , JK-триггер не имеет запрещенных комбинаций входных сигналов, которые следовало бы исключать при работе цифровых схем.

Его характеристическое уравнение имеет вид: Q(t+1) = K(t) Q(t) J(t) Q(t)
J(t) |
K(t) |
Q(t) |
Q(t+1) |
S(t) |
R(t) |
||
|
|
|
|
|
|
|
|
0 |
- |
0 |
0 |
0 |
- |
|
|
1 |
- |
0 |
1 |
1 |
1 |
|
|
- |
1 |
1 |
0 |
- |
0 |
|
|
- |
0 |
1 |
1 |
- |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначение
В базисе Шеффера |
В базисе Пирса |
|
|

§ 2. Регистры.
Определение: Регистры предназначены для хранения двоичной информации и в ряде случаев для выполнения логических операций над входными словами (
, , ,… ).
1)Приём слов:
-Прямой код
-Инверсный код
-Монофазный код
2)Функция:
-Установка в “0” или “1”
-Занесение констант
3)Выдача информации
Монофазный и парафазный код
-Инверсный код
4)Выполнение информации:
Статический регистр – когда отсутствуют различные связи (поразрядные операции)
При наличии межразрядных связей могут осуществляться операции сдвига , при этом при занесении и выдаче информации возможны следующие варианты построения регистров.
Сдвигающий регистр |
– если он сдвигает . |
Реверсивный регистр |
– если сдвигает и влево и вправо. |
Кольцевой регистр – если сдвигает по кольцу. Универсальный регистр – если делает всё .
Обозначение регистров – RG <ИМЯ>

у1:=RG:=0 y2:=RG:=ШД y3:=RG:=const y4:=ШД:=RG y5:=RG:=L2RG y6:=RG:=R1RG y7 ,y8:=RG:=R1RG
§ 2.1. Выполнение логических операций на статических регистрах.
Асинхронный JK – триггер.
Статический регистр не имеет межрегистровых связей.
Q(t+1) = J Q K Q
Q(t+1) = b * y п р * Q (y у c т b * y о б р ) * Q =
=b * y п р * Q y у c т * b * y о б р * Q =
=b * y п р * Q y у c т * Q * b * y у с т * Q * y о б р .
y п р |
y о б р |
y у с т |
Q(t+1) |
F |
|
|
|
|
|
0 |
0 |
0 |
Q |
Хранение |
|
|
|
|
|
0 |
0 |
1 |
0 |
Сброс(установка в “0”) |
|
|
|
|
|
0 |
1 |
0 |
bQ |
Конъюнкция |
|
|
|
|
|
0 |
1 |
1 |
0 |
Сброс |
|
|
|
|
|
1 |
0 |
0 |
b Q |
Дизъюнкция |

1 |
0 |
1 |
|
|
|
Запрет по Q |
||
|
|
|
bQ |
|
||||
1 |
1 |
0 |
b |
Запись |
||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
bQ |
|
|
|
||
Запрет по Q
Qb Q = Q (b 1)
Парафазный код:
Монофазный код:
§2.2. Вывод информации из регистров.

Проблема :
1)Вывести вовремя;
2)Обработку вывода нужно
Для случая монофазного кода
Ставится задача: выдать на выход прямой или обратный код
W=YпрQ
W=YобрQ
W=Yпр Q YобрQ – вывод информации из регистра
Ограничение: Нельзя подавать Упр и Уобр вместе ,т.к.Упр*Уобр=0
Wпр.=Yпр.Q Wобр=Yпр.Q
Wобр=YобрQ Wобр=YобрQ
§3. ДЕШИФРАТОРЫ
Обозначение:DC<имя>
Дешифратор-это комбинационная схема имеющая n-входов и n=2ⁿ - выходов
.Причем каждой n-разрядной входной комбинации будет соответствовать возбуждение только одной вполне определенной выходной цепи.

Обозначение на схемах:
Существует целая группа дешифраторов у которых число выбранных состояний меньше чем N:
K<N=2ⁿ ,где к- число возможных комбинаций.
§3.1. линейные дешифраторы
Пусть переменная Х=х1 х2 будет иметь две входные переменные
У0=Х2Х1
У1=Х2Х1
У2=Х2Х1
У3=Х2Х1
Таблица функционирования:
Х2 |
Х1 |
У0 |
У1 |
У2 |
У3 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
Схема:
На вход подаются парафазные коды

Y0
Y1
Y2
Y4
Обозначение:
Х1 у1 ДС
У2
Х2
у3
ОЕ у4
§3.2. параллельные дешифраторы
Предположим что Х будет состоять из входных аргументов х1,х2,х3
У1 =  3
3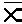 2
2 1 У2=
1 У2=  3
3  2
2 1
1

У3 =  3
3  2
2 1 У4 =
1 У4 =  3
3  2
2 1 У5 =
1 У5 = 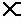 3
3  2
2  1 У6 =
1 У6 =  3
3  2
2  1 У7 =
1 У7 =  3
3  2
2  1 У8 =
1 У8 =  3
3  2
2  1
1
Имея общую часть для каждой пары можно переключать первую цифру. Схема:
При увеличении пирамиды происходит переключение отдельных элементов. Поэтому вход не может выдержать большого количества разветвлений. Потому существует существуют ограничения и требуется другая схема.
Самой старшей ступенью считается :
N = 2n + 2n-1+ 2n-1 + … + 22 = 4( 2n-1 – 1 ) S = 8 (2n-1- 1 )
τ дc = ( n –1 ) τ
Задержка растёт по мере увеличения ступеней.

§3.3. ступенчатые (матричные) дешифраторы.
Число входов дешифратора n делят на две части.
Если n – чётная , тогда в каждой части будет по n /2 входов.
Если n – нечётная , тогда в одной части будет по (n-1) /2 входов, а в другой (n + 1) /2
Для каждой части строят свой ДC по рассмотренным ранее принципам , а затем выходы этих двух ДС подключают попарно на двух входах коньюнкторов.
Выходы ДС образуют линию строк и столбцов.
ДC 4x16.
§3.4. Неполные дешифраторы
Идёт речь о ДС , число выходов k у которых будет меньше 2n = N
Здесь использование не всех входных и выходных комбинаций позволяет сократить оборудование.
