
Физика 1 семестр - Механика
.pdf
Конспект лекций по Физике |
для студенческих групп |
Z3111, Z3221, Z3442k, Z3532k |
21 |
||||||
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
A = (F r ), |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r = ϕ R , |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
A = (F |
ϕ R ). |
|
|
|
|
r |
|
|
По свойству смешанного |
|||
R |
|
|
|
|
|
||||
|
|
|
|
|
|
произведения векторов |
|||
|
|
|
|
|
|
|
|
|
|
Рис.20. К определению работы |
|
A = ( ϕ RF ) = ( ϕ M ). |
|||||||
по вращению АТТ |
|
|
|
Таким образом, имеем |
|||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = (M ϕ ). |
|
(61) |
|||
Мощность вращения АТТ можно найти, поделив формулу (61) на t |
|||||||||
|
|
A |
|
|
ϕ |
|
|
|
|
N = |
|
|
= |
M |
|
= |
(M ω ). |
(62) |
|
|
|
|
|||||||
|
|
t |
|
|
t |
|
|
|
|
Кинетическая энергия АТТ. Пусть тело вращается вокруг закрепленной оси. Разобьем его на элементарные области, каждую из которых в даль-
нейшем будем считать материальной точкой с массой mi. Каждая точка тела движется по окружности со своим собственным радиусом Ri.
Центры всех окружностей лежат на оси вращения. Все точки тела имеют одну и ту же угловую скорость ω. Линейную скорость каждой точки тела можно найти, воспользовавшись формулой (14): υi = ωRi .
υi
mi
Ri
О
Рис.21. Вращение элементарного фрагмента АТТ
Конспект лекций по Физике |
|
для студенческих групп Z3111, |
Z3221, Z3442k, |
Z3532k |
22 |
|||||||||
Кинетическая энергия элементарного фрагмента АТТ равна |
|
|
||||||||||||
|
E |
|
= |
miυi2 |
= |
mi Ri2ω2 |
. |
|
|
(63) |
||||
|
K i |
|
|
|
|
|||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Кинетическая энергия, связанная с вращением всего тела, равна |
|
|
||||||||||||
Ekвр = ∑ |
mi Ri2ω2 |
= ω2 |
∑ mi Ri2 = |
Iω2 |
. |
(64) |
||||||||
|
2 |
|||||||||||||
i |
|
|
|
2 |
|
2 |
i |
|
|
|
||||
Если тело движется поступательно со скоростью υ, и одновременно вращается вокруг оси, проходящей через центр масс с угловой скоростью ω, то полная кинетическая энергия равна сумме величин, задаваемых формула-
ми (46) и (64)
E |
|
= |
mυ 2 |
+ |
Iω2 |
. |
(65) |
k |
|
|
|||||
|
2 |
2 |
|
|
|||
|
|
|
|
||||
Теория Относительности.
Постулаты Эйнштейна
1.Скорость света в вакууме не зависит от выбора инерциальной системы отсчета и всегда равна с = 3·108 м/с.
2.Все физические процессы протекают одинаково для наблюдателей в любой инерциальной системе отсчета.
Первый из этих постулатов противоречит преобразованиям Галилея для скоростей (26), однако подтверждается астрономическими наблюдениями и специально проведенными оптическими экспериментами.
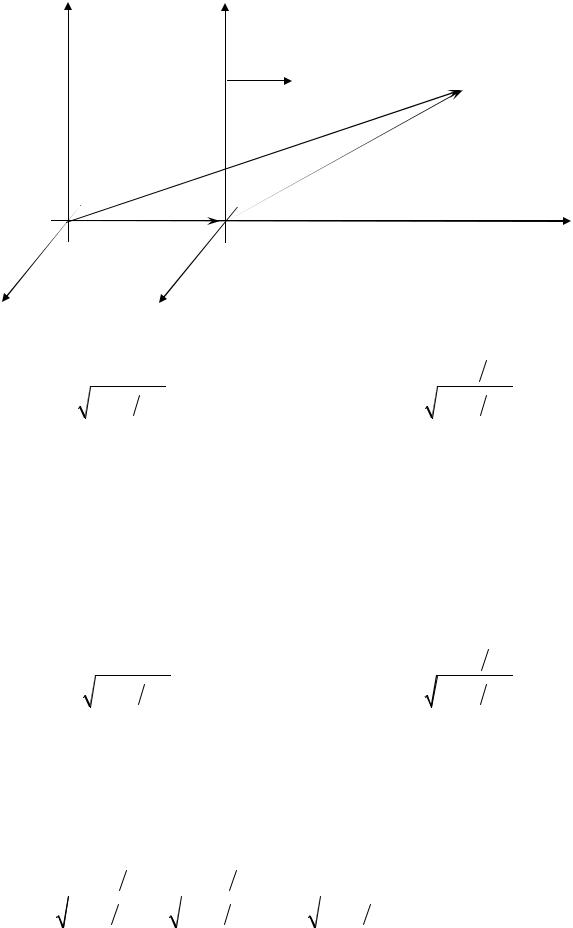
Преобразования Лоренца.
Преобразования Лоренца связывают координаты тела и время в двух разных инерциальных системах отсчета (рис.22). Одна из них – система K покоится, а вторая – система K’ движется относительно первой с постоянной скоростью υ. Будем считать, что скорость υ направлена вдоль оси (ох), и в начальный момент времени координатные оси двух систем совпадали.
Конспект лекций по Физике для студенческих групп |
Z3111, Z3221, Z3442k, Z3532k |
23 |
y |
y’ |
|
|
K |
K’ |
υ |
A |
r
r '
|
|
|
|
|
|
|
|
|
|
|
x, x’ |
|
|
|
R =υt |
|
|
|
|
|
|
||||
z |
|
|
z’ |
|
|
|
|
|
|
|
||
Рис. 22. Неподвижная и подвижная системы отсчёта |
|
|
|
|
||||||||
x¢ = |
|
x -υ t |
|
|
; |
y '= y ; |
z¢ = z ; |
t¢ = |
t -υ x c2 |
|
. (66) |
|
|
|
|
|
|
|
|
||||||
|
1 - (υ c)2 |
|
|
|
1 - (υ c)2 |
|
|
|||||
–Координаты и время оказались завязанными друг с другом.
–Время в различных инерциальных системах отсчета течет по-разному.
–Поперечные координаты для наблюдателей из разных инерциальных систем отсчета одинаковы.
Обратные преобразования Лоренца получаются из прямых при изме-
нении направления скорости υ и при замене всех штрихованных величин на не штрихованные, а не штрихованных – на штрихованные.
x = |
|
x′ +υ t |
|
; |
y = y¢; |
z = z¢; |
t = |
t |
′ +υ x c2 |
|
. (67) |
|
|
|
|
|
|
|
|||||||
1 - (υ c)2 |
1 - (υ c)2 |
|||||||||||
|
|
|
|
|
|
|
|
|||||
Следствия из преобразований Лоренца.
1. Относительность одновременности.
Два события, которые происходят для наблюдателя в системе К одновременно
( t = 0, |
но x ¹ 0) , для наблюдателя в системе К’ |
происходят не одновременно. |
||||||||||||
t¢ = |
t -υ x c2 |
|
= |
0 |
-υ x c2 |
|
= |
-υ x |
|
|
¹ 0; |
t¢ ¹ 0. (68) |
||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 - (υ c)2 |
|
|
1 - (υ c)2 |
|
|
c2 × 1 - (υ c)2 |
|
|||||
Конспект лекций по Физике для студенческих групп |
Z3111, Z3221, Z3442k, |
Z3532k |
24 |
||
2. Сокращение продольных размеров быстро движущихся тел: |
|
|
|||
ℓ = ℓ0 |
|
. |
|
|
|
1− (υ / c)2 |
|
(69) |
|
||
В этой формуле ℓо – собственная длина, т.е. длина, измеренная в той системе отсчета, относительно которой тело покоится.
Собственная длина всегда максимальна.
3. Замедление хода часов в быстро движущихся системах отсчета:
τ = |
τ 0 |
|
1 − (υ / c)2 . |
(70) |
В этой формуле τо – собственное время, т.е. время, измеренное в той системе отсчета, относительно которой тело покоится.
Собственное время всегда минимально.
4. Закон сложения скоростей:
|
|
|
|
′ |
= |
|
|
u ±υ |
|
|
|
|
|
|
|
u |
1 |
± (uυ c2 |
) . |
(71) |
|||||
|
|
|
|
|||||||||
Здесь |
u и |
υ – скорости двух объектов для неподвижного наблюдателя, |
||||||||||
u’ |
– |
скорость этих объектов друг относительно друга. В формуле знак |
||||||||||
минус, если скорости u и |
υ направлены в одну сторону, |
плюс – если в |
||||||||||
разные. |
|
|
|
|
|
|
|
|
|
|
||
Следствия из формулы (71) |
|
|
|
|
|
|
|
|
|
|||
– |
Если любая из скоростей |
|
u или υ есть скорость света в вакууме с, |
|||||||||
|
то в результате сложения получится |
u′ = c . |
|
|||||||||
– |
Если u < c и υ < c , то обязательно |
|
u′ < c . |
|
||||||||
5. Интервал |
S (между событиями) состоит из двух частей – |
из временной |
||||||||||
и пространственной: |
|
|
|
|
|
|
|
|
|
|||
|
|
|
S 2 = (c t )2 |
− ( x2 |
+ |
y2 + z2 ). |
(72) |
|||||
Интервал инвариантен относительно преобразований Лоренца, т.е. одинаков для наблюдателей в любой инерциальной системе отсчета.
Если временная часть больше пространственной, т.е. S 2 > 0, а S -
действительное число, то такой интервал называется временеподобным.
Конспект лекций по Физике для студенческих групп |
Z3111, Z3221, Z3442k, Z3532k |
25 |
Можно выбрать такую систему отсчета, в которой интервал сведется к измерению промежутка времени между двумя событиями.
Если пространственная часть больше временной, т.е. S 2 < 0, а S -
мнимое число, то такой интервал называется пространственноподобным. Можно выбрать такую систему отсчета, в которой интервал сведется к измерению расстояния между двумя одновременными событиями.
Если два события связаны друг с другом временеподобным интервалом, то одно из них может быть (может и не быть) следствием другого. Если два события связаны пространственноподобным интервалом, то ни одно из них не может быть следствием другого.
6.Импульс в теории относительности записывается так же, как и в классической механике (28)
p = mυ , |
(72) |
но понятие массы при этом наполняется новым содержанием
m = |
m0 |
|
1 − (υ c)2 . |
(73) |
В этом выражении mo – масса покоя, т.е. масса тела, измеренная в инерциальной системе отсчета, относительно которой тело покоится.
Масса покоя всегда минимальна.
7. В теории относительности вводится понятие энергии покоя
E = m c2. |
(74) |
|
0 |
0 |
|
Энергия покоя – это минимальная энергия, которую нужно затратить для “ рождения” частицы.
8. Полная энергия в теории относительности равна
E = m c2 . |
(75) |
Она включает в себя кинетическую энергию, потенциальную энергию и энергию покоя. Потенциальной энергией обычно пренебрегают.
9. Кинетическая энергия в теории относительности равна
E = m c2 |
− m c2 . |
(76) |
k |
0 |
|
10. Полная энергия, энергия покоя и импульс тела связаны соотношением:
E2 = p2 c2 + E2 . |
(77) |
0 |
|
Конспект лекций по Физике для студенческих групп |
Z3111, Z3221, Z3442k, Z3532k |
26 |
Инварианты теории относительности.
Инвариантами называются величины, которые одинаковы для наблюдателей в различных инерциальных системах отсчета.
1. |
Скорость света в вакууме – с. |
2. |
Интервал между событиями – S . |
3.Собственная длина – ℓ0 .
4.Собственное время – τ 0 .
5.Масса покоя – mo.
6.Энергия покоя – Eo.
7.Электрический заряд – q.
8.Количество вещества в молях – ν.
9.Безразмерные величины, обозначающие количество чего-либо.
