
- •Примеры базисов
- •Интегрирование
- •Определение
- •Аддитивная граница
- •25. Вероятность ошибки при оптимальном приеме в канале со случайной фазой
- •26. Относительная фазовая модуляция
- •27. Распределения Релея и Райса
- •28. Канал с замираниями. Модель с рассеивателями
- •32. Каналы с межсимвольной интерференцией. Оптимальный прием
- •Литература
32. Каналы с межсимвольной интерференцией. Оптимальный прием
Рассмотрим передачу по каналу с линейным фильтром, схема которого показана на рис 32.1.
Входной |
Выходной |
сигнал |
сигнал |
g(t) 
 +
+
АБГШ
Рис.32.1 Общая схема передачи по каналу с линейным фильтром
Здесь g(t) - импульсная переходная характеристика фильтра, описывающего
канал, n(t) - аддитивный белый гауссовский шум. Межсимвольная
интерференция возникает, когда сигнал проходит через линейный фильтр, частотная характеристика которого отлична от константы в полосе частот сигнала.
Предположим, что для передачи используются двоичные противоположные сигналы вида s0 (t) ! s(t) , s1 (t) ! s(t) , где s(t) - некоторая сигнальная функция, заданная на интервале [0,T ] . Рассмотрим передачу последовательности сигналов. Она может быть записана как
s(t, u) ! #u (l ) s(t lT ) ,
l
где величина u (l ) ! 1 однозначно определяется значением передаваемого двоичного символа по правилу 0 & %1, 1 & 1, а u - последовательность величин u (l ) . Положим, что длина передаваемой последовательности равна 2N и индекс l меняется в пределах от N до N 1, то есть
, u( N %1) ...,u ( 2) ,u ( 1) ,u (0) , u(1) ,u (2) ,...,u ( N 1) ) .
Обозначим сигнал на выходе фильтра канала (отклик канала на последовательность s(t,u) ) как x(t, u) . Очевидно, что x(t, u) ! s(t, u) g(t) , где
- обозначение свертки, или
) |
|
) |
|
x(t, u) ! ( s(t , u)g( )d ! #u(l ) ( s(t lT )g( )d ! #u (l ) h(t lT ) , |
|||
) |
l |
) |
l |
)
где h(t) ! ( s(t )g( )dt ! s(t) g(t) . Иначе говоря, функция h(t) представляет
)
собой отклик фильтра канала на входной сигнал s(t) . Функция h(t) может также рассматриваться как импульсная переходная характеристика пары “модулятор-фильтр канала”.
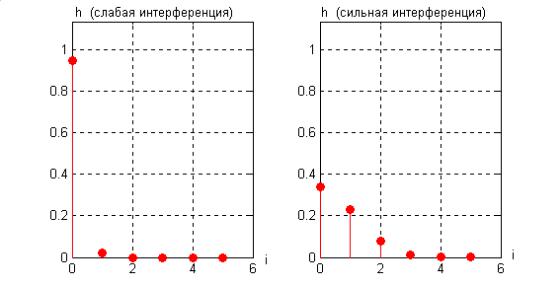
Пример. Пусть сигнальная функция s(t) , задана в виде прямоугольного импульса. Рассмотрим два примера канала: с относительно широкой и относительно узкой полосой, то есть с относительно слабой и относительно сильной интерференцией соответственно. На рис.32.2 приведены графики импульсной переходной характеристики канала g(t) для двух примеров каналов. Там же показаны графики функции h(t) для этих каналов.
Рис.32.2 Примеры импульсной переходной характеристики канала g(t) и импульсного отклика пары “модулятор-фильтр канала” h(t) .
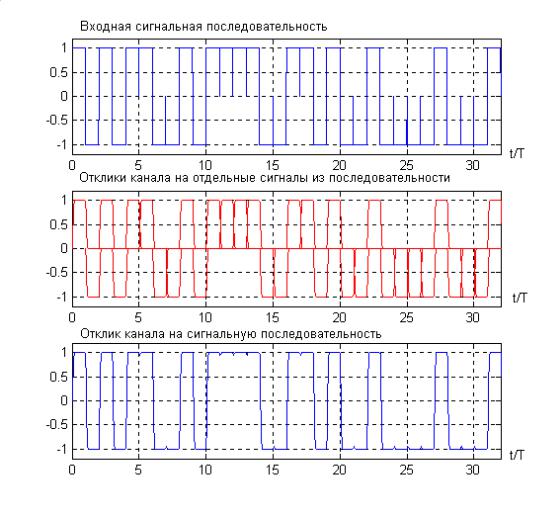
Видно, что при слабой интерференции функция h(t) слабо отличается от сигнальной функции s(t) . Иными словами, широкополосный канал вносит небольшие линейные искажения, приводящие к слабой межсимвольной интерференции.□
Сигнал на выходе канала с интерференцией может быть записан как
N 1 |
|
r(t) ! x(t,u) % n(t) ! #u(l ) h(t lT ) % n(t), ) + t + %) , |
(32.1) |
l !N
где n(t) - аддитивный белый гауссовский шум (АБГШ) со спектральной плотностью мощности N0 / 2 .
Пример (продолжение). На рис.32.3 и 32.4 показано влияние фильтра канала на переданную последовательность x(t,u) в случае слабой и сильной интерференции соответственно. Каналы со слабой и с сильной интерференцией определены так же как в начале примера (см. рис. 32.2).
Рис.32.3 Влияние фильтра канала на передаваемую последовательность. Случай слабой интерференции.
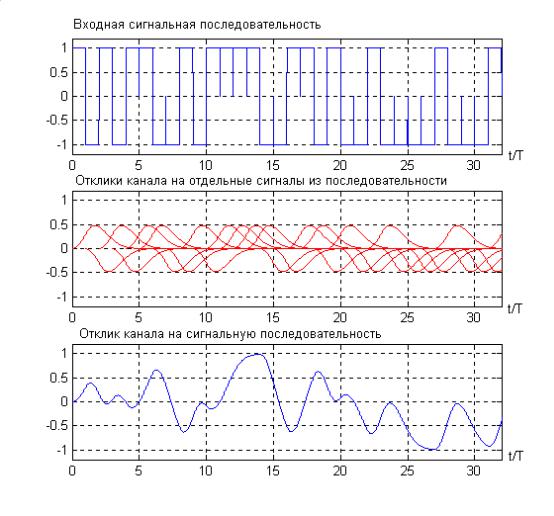
Рис.32.4 Влияние фильтра канала на передаваемую последовательность. Случай сильной интерференции.
Видно, что в канале со слабой интерференцией отклик канала практически совпадает с входной сигнальной последовательностью (см. рис.32.3). В канале с сильной интерференцией различие между входной последовательностью и откликом на нее становится очень заметным. Отметим, что графики, приведенные на рис.32.3 и 32.4 , не содержат аддитивного шума. □
Рассмотрим задачу построения оптимального приемника для канала с интерференцией. Поскольку при прохождении по каналу с интерференцией символы сигнальной последовательности оказывают взаимное влияние, то естественным становится рассмотрение оптимального приема последовательности сигналов, а не одиночного сигнала, как это делалось ранее. Обратимся вновь к равенству (32.1). Нетрудно заметить, что число различных
функций x(t, u) конечно и равно числу различных последовательностей u , то
есть равно 22 N . Пусть x(u) и r - коэффициенты разложения функций x(t, u) и
r(t) по некоторому ортогональному базису, размерность которого ограничена сверху величиной 22 N . Решение по максимуму правдоподобия относительно последовательности u формируется по правилу
! ! arg max (r | x(u)) , u w
u
где w(, | ,) - условная плотность вероятностей, задающая аддитивный шум,
действующий в канале. Для канала с АБГШ это правило может быть переписано в виде
! |
|
|
|
|
|
|
r x(u) |
|
|
|
2 |
! arg min− |
|
x(u) |
|
2 |
2−x(u),r... |
|
|||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
u ! arg min |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
Используя свойства разложения сигналов по ортогональному базису, |
можно |
||||||||||||||||||||||||
записать, что |
|
|
|
x(u) |
|
|
|
2 |
! )( x2 (t,u)dt |
|
|
и −x(u),r.! )(x(t,u)r(t)dt . Тогда |
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
) |
|
|
|
||||
! |
|
|
|
4 |
) |
|
|
|
|
|
) |
|
|
|
|
1 |
|
||||||||
! arg minu |
2 |
( x |
2 |
|
|
|
|
|
|
|
|
|
/ |
(32.2) |
|||||||||||
|
|
|
|
u |
2 |
|
|
(t,u)dt 2 ( x(t,u)r(t)dt /. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
) |
|
|
|
|
|
) |
|
0 |
|
|||
Рассмотрим по отдельности интегралы из правой части (32.2).
) |
) |
N 1 |
( x2 (t,u)dt ! |
( |
#u (k ) h(t lT ) |
) |
) k ! N |
|
N 1 N 1
! # # u( k ) u( j ) k ! N j! N
N 1
#u ( j ) h(t jT ) dt !
j ! N
)(h(t kT )h(t jT )dt !
)
N 1 N 1
# #u( k ) hk j u ( j) ! uHuT , k ! N j!N
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hk j |
! )(h(t kT )h(t jT )dt ! hj k , |
(32.3) |
||||||||||||
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
а H - матрица 2N 5 2N с элементами hk j , или в явном виде |
|||||||||||||||
|
|
|
|
; |
|
h0 |
|
h1 |
|
h2 |
... |
h2 N 1 |
8 |
||
|
|
|
|
9 |
|
h |
|
h |
|
h |
... |
h |
2 N 2 |
6 |
|
H ! [h |
|
|
! |
9 |
|
1 |
|
0 |
|
1 |
|
|
6 |
||
|
] |
9 |
|
h |
|
|
h |
|
h |
... |
h |
6. |
|||
k j |
|
|
9 |
|
|
2 |
|
1 |
|
0 |
|
|
2 N 3 |
6 |
|
|
|
|
|
9 ... |
... |
|
... ... |
|
... |
6 |
|||||
|
|
|
|
9 |
h |
2 N |
1 |
h |
h |
2 N 3 |
... |
|
h |
6 |
|
|
|
|
|
: |
|
2 N 2 |
|
|
|
0 |
7 |
||||
Величины hi называются коэффициентами межсимвольной интерференции.

Далее имеем,
) |
) |
N 1 |
|
|
( x(t,u)r(t)dt ! |
( |
#u (k ) h(t kT )r(t)dt ! |
|
|
) |
) k ! N |
|
|
|
|
|
1 |
) |
1 |
|
|
N |
|
N |
|
|
! # u (k ) (r(t)h(t kT )dt ! |
#r (k ) u (k ) ! −<,u., |
|
|
|
k ! N |
) |
k ! N |
где r ( k ) ! )(r(t)h(t kT )dt, и < !(r ( N ) , r ( N %1) ,..., r ( N 1) ) .
)
Для того, чтобы дать интерпретацию величины r (k ) рассмотрим свертку r(t) и некоторой функции c(t)
r(t) * c(t) ! )(r( )c(t )d .
)
Легко видеть, что если положить c(t) ! h( t), то можно записать, что
)
r ( k ) ! (r(t)h(t kT )dt ! r(t) * h( t) t !kT .
)
Это значит, что величины r (k ) представляют собой отсчеты сигнала на выходе фильтра, согласованного с h(t) , взятые в моменты kT . Оптимальное решение относительно последовательности u , основанное на рассмотрении принятой последовательности < , принимается по правилу
! |
(32.4) |
u ! arg max − uHuT % 2−<,u... |
u={ 1}2 N
Схема оптимального приемника последовательности, переданной по каналу с межсимвольной интерференцией, показана на рис.32.5.
r(t) |
|
|
r |
(k ) |
< |
|
! |
||||||||
|
|
|
|
|
|
|
|
|
|
u |
|||||
|
|
|
|
|
|
|
|
|
Формирование |
|
|
Вычисление |
|
|
|
|
|
|
|
|
|
|
|
|
последовательности |
|
|
− uHuT % 2−<,u.. |
|
|
|
|
h( t) |
|
|
|
|
|
|
|
! |
|
|
||||
|
|
|
|
|
|
|
|
отсчетов |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
u ! arg max |
|
|
|||
|
|
|
t ! kT |
|
|
|
< ! {r ( k ) } |
|
u={ 1}2 N |
|
|
|
|||
Фильтр, |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
согласованный |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
с функцией h(t) |
|
|
|
|
|
|
|
|
|
|
|||||
Рис.32.5 Схема оптимального приема последовательности при передаче по каналу с межсимвольной интерференцией
Для величин hi , определенных равенством (32.3), справедливо равенство hi ! h i . Предположим, что hi ! 0 при i > L , где L ++ N . Это означает, что интерференция распространяется на конечное число соседних символов. При
таком предположении |
матрица H имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
H ! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
; h0 |
h1 |
... hL 2 |
hL 1 |
|
0 |
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
0 |
0 |
||||||||
9 |
h |
h |
h |
... |
h |
L 2 |
h |
L 1 |
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
0 |
0 |
|||||
9 |
|
1 |
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
9 ... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
|
... |
|
... |
... |
|||||||||||||
9 |
|
|
|
.. |
h1 |
h0 |
h1 |
... |
hL 2 |
hL 1 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
0 |
0 |
||||||
9hL 2 |
|
|
|
|
|
|
|
|||||||||||||||||||||
9h |
L 1 |
h |
L 2 |
... |
h |
h |
h |
... |
h |
L 2 |
h |
|
0 |
|
0 |
|
|
0 |
|
0 |
0 |
|||||||
9 |
|
|
|
|
|
1 |
|
0 |
|
1 |
h1 |
|
|
L 1 |
hL 1 |
|
|
|
|
|
|
|
|
|
||||
9 |
|
0 |
hL 1 |
hL 2 ... |
h1 |
h0 |
... |
hL 2 |
|
0 |
|
|
0 |
|
0 |
0 |
||||||||||||
9 |
|
0 |
|
0 |
h |
L 1 |
h |
L 2 |
... |
h |
h |
h |
.... |
h |
L 2 |
h |
L 1 |
|
0 |
|
0 |
0 |
||||||
9 |
|
|
|
|
|
|
|
|
|
1 |
0 |
|
1 |
|
|
|
|
hL 1 |
|
|
||||||||
9 |
|
0 |
|
0 |
|
0 |
hL 1 |
hL 2 .... |
h1 |
h0 |
h1 |
... |
hL 2 |
0 |
0 |
|||||||||||||
9 |
|
0 |
|
0 |
|
0 |
|
0 |
h |
h |
L 2 |
... |
h |
h |
h |
... |
|
h |
L |
2 |
h |
0 |
||||||
9 |
|
|
|
|
|
|
|
|
|
L 1 |
|
|
|
1 |
|
0 |
|
1 |
|
|
|
|
L 1 |
|
||||
9 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
hL 1 |
hL 2 ... |
h1 |
h0 |
h1 |
|
... |
|
hL 2 |
hL 1 |
||||||||
9 |
|
|
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
|
... |
|
... |
... |
|||||||||||
9 ... |
|
|
||||||||||||||||||||||||||
9 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
0 |
h |
L 1 |
h |
L 2 |
... |
h |
|
h |
|
h |
... |
||||
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
|
1 |
|
||
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
0 |
|
0 |
hL 1 |
hL 2 |
... |
|
h1 |
|
h0 |
h1 |
||||||
9 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
9 ... |
... |
... |
... |
... |
... |
... |
.... |
... |
... |
... |
|
... |
|
... |
... |
|||||||||||||
9 |
|
0 |
... |
|
0 |
|
0 |
|
0 |
|
0 |
0 |
|
0 |
|
0 |
|
0 |
hL |
1 |
hL |
|
2 |
... |
h1 |
|||
9 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
... |
|
0 |
|
0 |
|
0 |
|
0 |
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
hL 1 |
hL 2 ... |
||||||
: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Ввиду симметричности матрицы H квадратичная форма uHuT в (32.4) может быть представлена в виде удвоенной суммы слагаемых, относящихся к верхней треугольной матрице, сложенной с суммой слагаемых по диагонали, то есть
N 1 N 1 |
|
N 1 k 1 |
|
|
N |
1 |
|
|
uHuT ! # #u (k ) hk j u ( j) ! 2 # #u (k ) hk j u ( j) % |
#(u( k ) )2 h0 ! |
|
||||||
k ! N j! N |
|
k ! N j! N |
|
|
k !N |
|
|
|
|
|
|
|
N 1 |
|
N 1 |
k %N |
|
|
|
|
|
! #(u (k ) )2 h0 % 2 # u (k ) #hi u (k i) . |
||||
|
|
|
|
k ! N |
|
k ! N |
i!1 |
|
Поскольку u (k ) ! 0 при k + N , и h ! 0 при i > |
L , то |
|
|
|||||
|
|
i |
|
|
|
|
|
|
N 1 |
4 |
|
|
|
L 1 |
1 |
|
|
uHuT % 2−<, u. ! # |
2 |
2r (k ) u (k ) (u( k ) )2 |
h0 |
2u( k ) #hi u (k i) / |
! |
|
||
k !N 3 |
|
|
|
i!1 |
0 |
|
|
|
N 1 |
|
! #m(r (k ) ;u (k ) ,u (k 1) ,...,u (k L%1) ) |
(32.5) |
k ! N
... |
|
0 |
8 |
... |
|
0 |
6 |
|
6 |
||
... |
... |
6 |
|
... |
|
0 |
6 |
|
6 |
||
... |
|
0 |
6 |
... |
|
0 |
6 |
|
6 |
||
... |
|
0 |
6 |
... |
|
0 |
6 |
|
6 |
||
... |
|
0 |
6 |
|
6 |
||
... |
|
0 |
6 |
... |
|
0 |
6 |
|
6 |
||
h |
h |
L 1 |
6 |
L 2 |
|
6 |
|
... |
hL 2 6 |
||
... |
... |
6 |
|
h0 |
h1 |
6 |
|
6 |
|||
h |
h |
6 |
|
1 |
|
0 |
7 |
где использовано обозначение
|
L 1 |
|
|
m(r (k ) ;u (k ) , u(k 1) ,...,u (k L%1) ) ! 2r (k ) u (k ) (u( k ) )2 h0 2u (k ) #hi u( k i) . |
(32.6) |
||
|
i!1 |
|
|
Из формулы (32.5) следует, что |
|
|
|
! |
N 1 |
|
|
#m(r (k ) ;u (k ) ,u (k 1) ,..., u (k L%1) ) . |
(32.7) |
||
u ! arg max2 N |
|||
u={ 1} |
k ! N |
|
|
|
|
||
Максимизация в правой части равенства (32.7) соответствует максимизации суммы слагаемых, каждое из которых зависит от текущего значения отсчета на выходе согласованного фильтра r (k ) , текущего значения переданного символа u (k ) , и L 1 предыдущих значений переданных символов u(k 1) ,...,u( k L%1) .
Пример (продолжение). Вычислим величины h0 , h1 ,..., hL 1 для каналов с сильной и слабой интерференции. На рис. 32.6 они показаны в графической форме.
Рис.32.6. Коэффициенты интерференции для каналов с относительно слабой и относительно сильной интерференцией
Из этих графиков следует, что можно принять L ! 1 для канала со слабой интерференцией и L ! 3 для канала с относительно сильной интерференцией. Заметим, что значение L ! 1 означает отсутствие интерференции. Матрицы H для этих двух случаев имеют вид
|
|
|
;h0 |
|
0 |
0 |
" 0 |
8 |
|
|
||
|
|
|
9 |
0 |
|
h |
0 |
" 0 |
6 |
|
|
|
|
|
|
9 |
|
|
0 |
|
|
|
6 |
|
|
|
|
H ! 9 |
0 |
|
0 |
h0 |
" 0 |
6 |
|
|
||
|
|
|
9 |
|
|
|
|
|
|
6 |
|
|
|
|
|
9" " " " "6 |
|
|
|||||||
|
|
|
9 |
0 |
|
0 |
0 |
" h |
6 |
|
|
|
|
|
|
: |
|
|
|
|
|
0 |
7 |
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
;h0 |
h1 |
|
h2 |
0 |
0 0 |
" 0 8 |
|||||
|
9h |
h |
|
h |
h |
0 |
0 |
# |
0 |
6 |
||
|
9 |
1 |
0 |
|
1 |
2 |
|
|
|
|
|
6 |
|
9 |
|
h1 |
|
h0 |
h1 |
h2 |
0 |
# 0 |
6 |
||
|
9h2 |
|
6 |
|||||||||
H ! |
9 |
0 h2 |
|
h1 |
h0 |
h1 |
h2 |
# 0 |
6 |
|||
9 |
|
|
|
|
|
|
|
|
# # |
6 |
||
|
# # # # # # |
6 |
||||||||||
|
9 |
0 # |
|
0 h2 |
h1 |
h0 |
h1 |
h2 |
||||
|
9 |
|
6 |
|||||||||
|
9 |
0 |
# |
|
0 |
0 |
h |
h |
h |
h |
6 |
|
|
9 |
0 |
|
|
0 |
0 |
2 |
1 |
0 |
1 |
6 |
|
|
9 |
# |
|
0 |
h |
2 |
h |
h |
6 |
|||
|
: |
|
|
|
|
|
|
|
1 |
0 |
7 |
|
соответственно. Отсюда следует, что выражение (32.6) принимает вид
m(r (k ) ;u (k ) , u(k 1) ,...,u (k L%1) ) ! m(r (k ) ;u(k ) ) ! 2r (k ) u (k ) (u( k ) )2 h0 ! 2r (k ) u (k ) h0
для канала со слабой интерференцией, и
m(r (k ) ;u (k ) ,u (k 1) ,..., u( k L%1) ) ! m(r (k ) ;u (k ) ,u (k 1) , u( k 2) ) !
! 2r (k ) u (k ) (u (k ) )2 h0 2u(k ) (h1u( k 1) % h2 u(k 2) ) ! 2r (k ) u (k ) h0 2u (k ) (h1u (k 1) % h2u (k 2) )
для канала с сильной интерференцией. □ |
|
|
Назовем набор предыдущих L 1 значений |
(u( k L%1) ,...,u( k 1) ) состоянием |
|
некоторого конечного |
автомата. Нетрудно |
заметить, что величина |
m(r (k ) ;u (k ) ,u (k 1) ,...,u (k L%1) ) |
соответствует переходу |
|
(u( k L%1) ,...,u( k 1) ) & (u(k L%2) ,...,u(k ) )
Тогда максимизация в правой части (32.7) может быть интерпретирована как поиск пути с максимальной накопленной метрикой в решетке с 2L 1 состояниями, аналогичной кодовой решетке сверточного кода. Отыскание
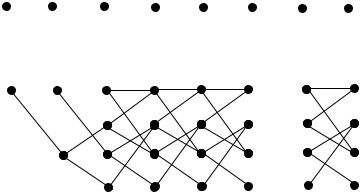
последовательности, имеющей максимальное значение метрики (32.7), может быть выполнено с использованием алгоритма Витерби.
Пример (окончание). Для двух рассматриваемых случаев имеем решетки следующего вида (см. рис.32.7).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
(а) |
|
|
|
|
||||
(u (k 2) , u(k 1) ) |
|
|
|
|
|||||||||||||||
+1+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
… |
+1-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(б) |
|
|
|
|
||||
Рис.32.7. Решетки для каналов со слабой (а) и сильной интерференцией (б).
Для канала со слабой интерференцией (практически без интерференции) “решетка” имеет только одно состояние. Это означает, что зависимости от предыдущих символов нет, и оптимальный прием состоит в одиночном приеме каждого сигнала. В этом случае понятие решетки вообще не нужно использовать для описания процедуры приема. В канале с относительно сильной интерференцией решетка имеет четыре состояния, задающие четыре возможных значения пары предыдущих символов (u (k 2) , u(k 1) ) , то есть (+1,+1), (+1,-1), (-1,+1) и (-1,-1). Алгоритм оптимального приема в этом случае может быть реализован с использованием алгоритма Витерби. Метрикой ребра,
соединяющего узлы (u (k 2) , u(k 1) ) и (u (k 1) ,u( k ) ) , будет значение, вычисляемое по формуле (32.7).□
33. Каналы с межсимвольной интерференцией. Оценка вероятности ошибки (предварительный вариант)
Рассмотрим передачу последовательности по каналу с межсимвольной интерференцией и прием по максимуму правдоподобия, реализованный в форме алгоритма Витерби.
Пусть
u # (u(! N ) , u( ! N 1) ,..., u(!2) , u( !1) , u(0) , u(1) , u(2) ,..., u( N !1) )
переданная последовательность, и
u' # (u'(! N ) , u'(! N 1) ,..., u'(!2) , u'( !1) , u'(0) , u'(1) , u'( 2) ,..., u'( N !1) )
некоторая другая последовательность, u u' , u(k ) , u'(k ) # %1. Обозначим через x(t, u) и x(t, u' ) отклики канала на переданные последовательности u и u' ,
x(t, u) # &u(l ) h(t ! lT ) ,
l
x(t, u' ) # &u'(l) h(t ! lT ) .
l
Обозначим также разложения функций x(t, u) и x(t, u' ) по некоторому
функциональному базису как x(u) и x(u' ) .
Последовательности u и u' соответствуют некоторым путям в решетке.
Определим вероятность того, что конкретный неправильный путь u' |
в решетке |
||||||||||||||||||||
будет выбран вместо правильного u . Вероятность этого события равна |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
! |
|
. |
x(u) ! x(u') |
+ |
|
|
|
(33.1) |
|||||
|
|
|
|
|
|
|
|
Pr u # u'| u( # Q, |
|
|
|
|
|
|
) . |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
, |
|
|
2N0 |
|
) |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|||
Квадрат расстояния между последовательностями x(u) и |
x(u') |
можно записать |
|||||||||||||||||||
как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(u) ! x(u') |
|
|
|
2 |
# |
0 |
(x(t, u) ! x(t, u' )) |
2 |
dt # |
0 |
. |
N !1 |
|
(k ) |
! u' |
(k ) |
|
+ |
2 |
|
|
|
|
(u |
)h(t |
|
||||||||||||||||
|
|
|
|
|
/ |
|
/ |
, |
& |
|
|
! kT ) ) dt # |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
− k #! N |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
!0 |
|
|
|
!0 |
|
|
|
|
|
|
|
|
||
! |
|
|
! |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||
|
N |
1 |
N |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
# & & (u(k ) ! u'(k ) )(u( j) ! u'( j) ) /h(t ! kT )h(t ! jT )dt # . |
|
|||||||||||||||||||
|
k #! N j#! N |
|
|
|
|
|
!0 |
|
|
|
|
|
|
|
|
||||||
N !1 N !1
# & &(u(k ) ! u'( k ) )hk ! j (u( j) ! u'( j) ) . k #! N j#! N
Определим ошибочную последовательность e # (e(!N ) , e(! N 1) ,..., e( N !1) ) , где
|
|
|
|
|
|
|
|
4 1, если u(k ) |
# 1, u'(k ) # !1 |
|
|||
|
(k ) |
|
1 |
|
(k ) |
|
(k ) |
1 |
|
( k ) |
|
(k ) |
|
e |
|
# |
|
(u |
|
! u' |
|
) # 3 0, если |
u |
|
# u' |
|
. |
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
1!1, если |
u(k ) |
# !1, u'(k ) # 1 |
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Тогда по аналогии с выводом равенства, непосредственно предшествующим формуле (32.3), с учетом симметричности матрицы H и конечного числа ненулевых коэффициентов интерференции {hi } можно получить, что
|
x(u) ! x(u') |
2 |
# 4eHeT |
|
N !1 . |
L!1 |
+ |
|
||
|
|
# 4 & ,(e(k ) ) 2 h0 |
2&e(k ) hi e(k !i) ) . |
|
||||||
|
|
|
|
|
|
|
k #! N − |
i#1 |
|
|
Вероятность (33.1) может быть записана как |
|
|
|
|||||||
|
|
|
|
|
! |
|
|
|
|
(33.2) |
|
|
|
|
|
Pr u # u'| u(# PE (e) , |
|
|
|||
где |
|
|
|
|
|
|
|
|
|
|
. |
2eHeT |
+ |
. |
2 |
N !1 . |
L!1 |
+ + |
(33.3) |
||
PE (e) # Q, |
|
|
) |
# Q, |
|
& ,(e(k ) ) 2 h0 |
2&e(k ) hi e(k !i) ) ) |
|||
, |
N0 |
|
) |
, |
N0 k #! N − |
i#1 |
) |
|
||
|
− |
|
|
− |
|
|
||||
- вероятность события, состоящего в том, что при передаче некоторой последовательности принято ошибочное решение в пользу другой
последовательности, определяемой последовательностью ошибок e . |
Равенства |
||||||||
|
|
|
|
|
|
! |
# u'| u( зависит только от |
||
(33.2) и (33.3) означают, что искомая вероятность Pr u |
|||||||||
значения ошибочной последовательности |
e |
и не |
зависит от |
значений |
|||||
последовательностей u и u' . |
|
|
|
|
|
|
|
|
|
Обозначим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L !1 |
|
|
||
mE (e(k ) , e( k !1) ,..., e(k ! L 1) ) # (e(k ) )2 h0 2&e(k ) hi e( k ! i) , |
|
||||||||
|
|
|
|
|
i #1 |
|
|
|
|
тогда можно записать, что |
|
|
|
|
|
|
|
|
|
. |
2 N !1 |
(k ) |
|
( k !1) |
|
(k !L 1) |
+ |
|
|
, |
&mE (e |
, e |
,..., e |
) |
(33.4) |
||||
PE (e) # Q, |
|
|
|
|
) ) . |
||||
− |
N0 k #!N |
|
|
|
|
|
|
|
|
Для подсчета вероятности PE (e) |
полезным оказывается использование |
||||||||
некоторого конечного автомата. Заметим, что он прямо не связан с конечным автоматом, описываемым решеткой, применяемой при приеме по алгоритму Витерби. Назовем набор предыдущих значений (e(k !L!1) ,..., e(k !1) ) состоянием
этого |
конечного |
автомата. |
Нетрудно |
заметить, |
что |
величина |
|||
mE (e(k ) , e(k !1) ,..., e(k !L 1) ) соответствует переходу |
|
|
|
|
|
||||
|
|
(e(k !L!1) ,..., e(k !1) ) 5 (e(k !L!1 1) ,..., e(k ) ) . |
|
|
|||||
При |
подсчете вероятности |
P (e) |
величину |
m |
E |
(e(k ) , e(k !1) ,..., e(k !L 1) ) можно |
|||
|
|
|
E |
|
|
|
|
|
|
рассматривать как метрику ребра в решетке (назовем ее решеткой ошибок) с 3L!1 состояниями, соответствующего этому переходу. Суммирование в правой части (33.4) при этом соответствует следованию вдоль некоторой траектории в решетке ошибок, соответствующей последовательности ошибок e .
Поскольку при оценке вероятности ошибки для алгоритма Витерби следует учитывать только те последовательности e , которые соответствуют ошибочным событиям, то далее будем полагать e именно такими. Напомним, что ошибочным событием при декодировании называется выбор пути в решетке, который соответствует петле, то есть один раз ответвляется от правильного пути и сливается с ним где-то далее. Нетрудно заметить, что ошибочное событие соответствует такой последовательности e , в которой ненулевая компонента стоит на некоторой, например, l -ой, позиции и далее не имеется L !1 нулей, следующих подряд. Обозначим множество таких последовательностей через E(l ) . Если предположить, что источник порождает символы u(k ) равновероятно и независимо, то вероятность появления конкретной последовательности ошибок равна 2!w(e) , где w(6) - обозначение
числа ненулевых элементов в последовательности. Тогда с использованием аддитивной границы имеем следующую оценку для вероятности ошибочного события в l -ом узле решетки канала
PE(l) 8 &2!w(e) PE (e) . |
(33.5) |
e7E( l ) |
|
Для вероятности ошибочного решения о переданном бите, возникающего вследствие ошибочного события в некотором узле, имеем границу вида
Pb(l ) 8 &w(e) 2!w(e) PE (e) . |
(33.6) |
e7E( l ) |
|
Рассмотрим вычисление границ (33.5) и (33.6). Заметим, что метрики ребер в решетке ошибок могут принимать лишь конечное число различных значений. Более того, они могут быть представлены в виде линейной комбинации
некоторых (базовых) констант взятых |
с |
целыми |
|
неотрицательными |
||||||||||
коэффициентами, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
m |
E |
(e(k ) , e(k !1) ,..., e(k !L 1) ) # w m(1) w |
m( 2) ... w |
K |
m |
( K ) , |
|
|
|||||
|
|
1 |
E |
2 |
E |
|
|
E |
|
|
|
|||
где m(1) ,..., m( K ) |
- базовые константы, |
K |
- их число, |
w |
|
, w |
2 |
,..., w |
K |
- целые |
||||
E |
E |
|
|
|
|
|
1 |
|
|
|
|
|||
неотрицательные коэффициенты, определяемые набором |
e(k ) , e(k !1) ,..., e(k !L 1) и |
|||||||||||||
коэффициентами интерференции {hi } . Набор базовых констант и их число,
очевидно, зависят от коэффициентов интерференции {hi } . Легко видеть, что
при любых значениях коэффициентов интерференции {hi } выполняется неравенство K 8 3L .
Введем формальный ряд (производящую функцию) вида
T (Z, N) # |
&a(w1 ,..., wK , n)Z w1mE(1) ... wK mE( K ) (N / 2)n , |
||||
|
|
w1...wK , n |
|
|
|
где a(w1,..., wK , n) - число петель в решетке ошибок, |
метрики которых равны |
||||
величине |
|
|
|
|
|
m |
(w ,..., w |
, n) #w m(1) w m( 2) ... w m( K ) , |
|||
E |
1 |
K |
1 E |
2 E |
K E |
а число ненулевых элементов в последовательности ошибок, соответствующих этой петеле, равно n . Тогда границы (33.5) и (33.6) можно выразить в виде
(l ) |
|
& a(w1 |
|
!n |
. |
2 |
|
|
+ |
|
|
8 |
,..., wK , n)2 |
, |
|
|
mE (w1 |
) |
, |
||||
PE |
|
Q, |
N0 |
,..., wK , n) ) |
|||||||
|
|
w1 ,...,wK ,n |
|
|
− |
|
|
|
|||
Pb(l ) 8 |
|
& na(w1 |
|
|
. |
2 |
|
|
+ |
||
1 |
,..., wK , n)2!n Q, |
mE (w1 ,..., wK , n) ) . |
|||||||||
|
K |
,n |
|
|
− |
N |
0 |
|
|
|
|
|
w |
,...,w |
|
|
, |
|
|
|
) |
||
Величины a(w1 ,..., wK , n) можно найти, анализируя диаграмму (граф) состояний ошибок.
В общем виде формула для определения производящей функции T (Z, N)
может быть найдена следующим образом. Определим 3L!1 93L!1 матрицу
переходов |
A(Z, N) # [aij |
(Z, N)] |
в диаграмме состояний. Элемент матрицы |
|||
aij (Z, N) # Z m (N / 2)n , |
если переход (ребро) |
i 5 j в диаграмме состояний |
||||
имеет метрику равную |
m |
и соответствует n |
ненулевым элементам в |
|||
последовательности ошибок. |
|
|
|
|||
Пусть 3L!1 9 3L!1 |
матрица переходов в диаграмме ошибок записана в виде |
|||||
|
|
|
|
? 1 |
a(Z, N) < |
|
|
|
|
A(Z, N) # = |
|
: , |
|
|
|
|
|
>b(Z, N) |
A1 (Z, N); |
|
где a(Z, N) |
- матрица-строка размера 19 (3L!1 !1) , |
b(Z, N ) - матрица-столбец |
||||
размера (3L!1 !1) 91, |
|
A1 (Z, N) - матрица |
(3L!1 !1) 9 (3L!1 !1) . Тогда |
|||
производящая функция T (Z, N) равна |
|
|
||||
0 |
|
|
T (Z, N) # a(Z, N )&A1 (Z, N )l b(Z, N) # a(Z, N) I ! A1 (Z, N)Α!1 b(Z, N) , |
||
l #0 |
|
|
где I - единичная матрица (3L!1 !1) 9 (3L!1 !1) . |
||
Рассмотрим примеры. |
|
|
Пример 1. Пусть |
L # 2 и коэффициенты интерференции равны h0 , h1 . |
|
Число состояний решетки ошибок |
и диаграммы состояний ошибок равно |
|
3L!1 # 3 . Состоянием |
называется |
набор (e(k !1) , e( k !2) ,...,e(k ! L 1) ) # (e( k !1) ) ; все |
возможные состояния это: 0, +, -. Здесь и далее при обозначении состояний для краткости используется обозначение: % вместо %1. Метрики ребер вычисляются по формуле
mE (e(k ) , e(k !1) ) # (e(k ) )2 h0 2e(k )h1e( k !1) .
Их значения перечислены в таблице 33.1
Таблица 33.1
e(k ) , e( k !1) |
mE (e(k ) , e(k !1) ) |
|
|
0,0 |
0 |
|
|
0,+1 |
0 |
|
|
0,-1 |
0 |
|
|
+1,0 |
h0 |
|
|
+1,+1 |
h0 2h |
|
|
+1,-1 |
h0 ! 2h |
|
|
-1,0 |
h0 |
|
|
-,1+1 |
h0 ! 2h |
|
|
-1,-1 |
h0 2h |
|
|
Матрица переходов из состояния в состояние в данном случае равна
0
01
1 ! 1
Z h0 Z h0 Z h0
N/ 2
2h1 N / 2 !2h1 N / 2
!
Z h0 N / 2
Z h0 !2 h1 N / 2 . Z h0 2 h1 N / 2
Тогда производящая функция может быть найдена как |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
T (Z, N) # Z |
h0 |
|
h0 |
|
|
. |
0 ? |
Z |
h0 2h1 |
N / 2 |
Z |
h0 !2 h1 |
N / 2 |
<l |
+ |
1 |
|
||||||||
N / 2 Z |
N |
|
, |
& |
= |
|
|
|
: |
) |
? |
< |
# |
||||||||||||
|
|
/ 2(, |
|
|
h0 !2h1 |
N / 2 |
Z |
h0 2 h1 |
|
|
) |
= |
: |
||||||||||||
|
|
|
|
|
|
− l #0 |
>Z |
|
|
|
N / 2; |
|
>1; |
|
|||||||||||
h |
|
h |
|
? |
|
|
h0 2 h1 |
N / 2 |
Z |
h0 !2h1 |
N / 2 |
< |
!1 1 |
|
|
|
|
||||||||
|
|
1! Z |
|
|
|
|
|
|
: |
|
? < |
# |
|
|
|||||||||||
# Z 0 N / 2 |
Z 0 N / 2(= |
|
h0 !2 h1 |
N / 2 |
1! Z |
h0 |
2h1 |
|
|
= : |
|
|
|||||||||||||
|
|
|
|
>Z |
|
|
|
|
|
N / 2; |
|
>1; |
|
|
|
||||||||||
(НЕ ЗАВЕРШЕНО!)
Пример 2. Пусть L # 3 и коэффициенты интерференции равны h0 , h1 , h2 .
Число состояний решетки ошибок и диаграммы состояний ошибок равно 3L!1 # 9 . Состоянием называется набор (e(k !1) , e(k !2) ,...e(k !L 1) ) # (e(k !1) , e( k !2) ) ; все
возможные состояния это: (0,0), (0,+1), (0,-1), (+1,0), (+1,+1), (+1,-1), (-1,0), (-1,+1), (-1,-1). Метрики ребер в решетке ошибок (диаграмме состояний)
вычисляются |
|
|
по |
|
|
формуле |
||
m |
E |
(e(k ) , e(k !1) , e(k !2) ) # (e(k ) ) 2 |
h |
2e(k ) h e(k !1) 2e( k ) h |
e(k !2) . |
Их |
значения |
|
|
|
0 |
1 |
2 |
|
|
|
|
перечислены в таблице 33.2 Удвоенная (с целью экономии места) матрица переходов из состояния в состояние равна
|
00 |
0 |
0 ! |
0 |
00 |
2 |
0 |
0 |
Z h0 |
0 |
2 |
0 |
0 |
Z h0 |
0 ! |
2 |
0 |
0 |
Z h0 |
0 |
0 |
2 |
0 |
0 |
|
0 |
2 |
0 |
0 |
! |
0 |
2 |
0 |
0 |
! 0 |
0 |
0 |
2 |
0 |
! |
0 |
0 |
2 |
0 |
! ! |
0 |
0 |
2 |
0 |
|
|
! |
N |
0 |
0 |
2 h2 N |
0 |
0 |
!2 h2 N |
0 |
0 |
|
Z h0 2 h1 N |
0 |
|
Z h0 2 h1 2h2 N 0 |
|
|
Z h0 2 h1 !2 h2 N 0 |
|
|
0 |
Z h0 !2h1 N |
|
0 |
Z h0 !2h1 2h2 |
|
0 |
Z h0 !2h1 !2h2 |
|
! 0 |
! |
|
Z h0 N |
0 |
|
Z h0 !2h2 N |
0 |
|
Z h0 2h2 N |
0 |
|
0 |
Z h0 |
|
0 |
Z h0 |
|
0 |
Z h0 |
|
0 |
0 |
N |
0 |
0 |
N |
0 |
0 |
|
! ! |
|
0 |
|
0 |
|
0 |
!2h1 N |
0 |
!2h1 !2h2 N |
0 |
!2h1 2h2 N |
0 |
|
Z h0 |
|
Z h0 |
|
Z h0 |
2h1 N
2h1 !2 h2 N
2h1 2 h2 N
Таблица 33.2
e(k ) , e( k !1) , e(k !2) |
mE (e(k ) , e(k !1) , e(k !2) ) |
0,0,0 |
0 |
0,0,+1 |
0 |
0,0,-1 |
0 |
0,+1,0 |
0 |
0,+1,+1 |
0 |
0,+1,-1 |
0 |
0,-1,0 |
0 |
0,-1,+1 |
0 |
0,-1,-1 |
0 |
+1,0,0 |
h0 |
+1,0,+1 |
h0 2h2 |
+1,0,-1 |
h0 ! 2h2 |
+1,+1,0 |
h0 2h1 |
+1,+1,+1 |
h0 2h1 2h2 |
+1,+1,-1 |
h0 2h1 ! 2h2 |
+1,-1,0 |
h0 ! 2h1 |
+1,-1,+1 |
h0 ! 2h1 2h2 |
+1,-1,-1 |
h0 ! 2h1 ! 2h2 |
-1,0,0 |
h0 |
-1,0,+1 |
h0 ! 2h2 |
-1,0,-1 |
h0 2h2 |
-1,+1,0 |
h0 ! 2h1 |
-1,+1,+1 |
h0 ! 2h1 ! 2h2 |
-1,+1,-1 |
h0 ! 2h1 2h2 |
-1,-1,0 |
h0 2h1 |
-1,-1,+1 |
h0 2h1 ! 2h2 |
-1,-1,-1 |
h0 2h1 2h2 |
(НЕ ЗАВЕРШЕНО!)
34. Совместное рассмотрение модуляции и кодирования
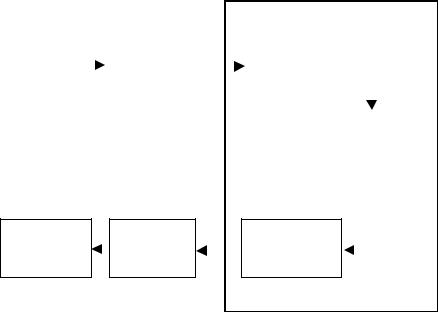
В этом разделе мы рассмотрим передачу с использованием помехоустойчивого кодирования (см. рис.34.1.)
Вообще говоря, существует много способов совместного выбора и/или согласования параметров модуляции, кодирования и алгоритмов
Источник |
|
|
Кодер |
|
|
|
|
|
|
s(t) |
дискретных |
|
|
канала |
|
|
|
|
Модулятор |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
||||||||
сообщений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Канал |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Декодер |
|
|
|
|
|
r(t) |
Получатель |
|
канала |
|
|
|
Демодулятор |
|
|
|
|
|
|
|
|
Дискретный
канал
Рис. 34.1 Схема системы передачи дискретных сообщений с использованием кодирования
декодирования. Рассмотрим наиболее простой из этих способов. |
|
|||||
Предположим, |
что |
источник |
порождает |
поток |
двоичных |
|
информационных |
символов. Блок из m , m ! 1, последовательных |
|||||
информационных |
двоичных |
символов может рассматриваться |
как одно из |
|||
q ичных значений, q # 2m . Эти значения объединяются в наборы из k
символов и кодируются q ичным блоковым кодом длины n , n ! k ! 1, с
минимальным расстоянием d . Пусть для передачи используется q ичное
множество сигналов, и отображение символов кодового |
слова |
в сигналы |
||||||
происходит очевидным образом: если символ кодового |
слова |
принимает |
||||||
значение i , |
i # 0,1,..., q 1, то |
передается сигнал |
si (t) . |
Эти |
сигналы |
|||
последовательно передаются по каналу, демодулируются, и |
на выходе |
|||||||
демодулятора |
образуется |
последовательность |
жестких |
|
|
решений |
||
(последовательность q ичных значений), которая поступает на вход декодера.
Относительно алгоритма декодирования предположим, что декодирование выполняется с исправлением всех ошибок, число которых t удовлетворяет условию
|
d 1 |
, |
если d нечетное |
|
|
|
2 |
||
|
|
. |
||
t ( & |
d |
|
|
|
|
1, |
если d четное |
||
|
2 |
|||
% |
|
|
|
|
Будем полагать, что ошибки в кодовых словах возникают независимо, то есть дискретный канал, образованный модулятором, каналом и демодулятором представляет собой дискретный канал без памяти. Это условие выполняется при использовании модуляции без памяти и канала с независимыми искажениями, например, канала с АБГШ, канала с АБГШ и случайной фазой, канала с замираниями при использовании достаточного перемежения.
Обозначим через Pe вероятность ошибки, возникающую при передаче одиночного сигнала. Она определяется видом модуляции и параметрами канала. Вероятность ошибочного декодирования одного кодового слова может быть оценена как
n |
|
Pe( word ) ( )Cni Pe i (1 Pe )n i , |
(34.1) |
i#t 1
где Cni # n!/(i!(n i)!) . При последовательной передаче многих кодовых слов декодирование иногда выполняется с ошибкой и при каждом ошибочном декодировании декодер выдает получателю несколько ошибочных символов.
Можно показать, что вероятность |
ошибки в потоке |
q ичных |
символов, |
формируемых декодером, может быть оценена как |
|
|
|
P( symbol ) |
+ (d / n)P( word ) . |
|
(34.2) |
e |
e |
|
|
Действительно, число ошибочных |
кодовых символов, |
возникающих при |
|
ошибочном декодировании одного слова, лежит в пределах от d |
до n . При |
||
ошибочном декодировании наиболее вероятным оказывается |
принятие |
||
решения в пользу слова отличного от переданного и находящегося на минимальном расстоянии от него. Отсюда следует формула (34.2).
Рассмотрим теперь вероятность ошибки на бит. Ранее было показано (см. выражение (19.4)), что вероятность ошибки на бит связана с вероятностью ошибки на символ соотношением
P |
(bit ) |
# |
|
|
2m 1 |
|
P |
( symbol ) |
, |
|
|
|
|
2m 1 |
|
|
|||||||
e |
|
|
|
e |
|
|
|
||||
где m # log 2 q . Отсюда с учетом формул (34.1) и (34.2) следует, что |
|
||||||||||
|
m 1 |
|
|
d |
n |
|
|
|
|
||
Pe (bit ) + |
2 |
|
|
|
)Cni Pe i (1 Pe )n i . |
(34.3) |
|||||
m |
|
|
|
||||||||
|
2 |
1 n i#t 1 |
|
|
|
|
|||||
Важной является зависимость вероятности ошибки на бит от отношения сигнал/шум на бит. При передаче с использованием q ичного кодирования со
скоростью R |
каждый сигнал |
переносит |
R log 2 q |
бит. Поэтому энергия, |
|||||||
приходящаяся |
на передачу одного бита, равна |
|
E /(R log 2 q) , где E - энергия |
||||||||
сигнала. Тогда отношение сигнал/шум на бит равно |
|
||||||||||
|
1 |
E |
. |
|
E |
1 |
|
|
|
||
|
/ |
|
, |
# |
|
|
|
|
|
. |
(34.4) |
|
|
|
|
|
|
|
|||||
|
/ |
N0 |
, |
|
N0 R log 2 |
q |
|
|
|||
|
0 |
−bit |
|
|
|
||||||
Чтобы явно указать зависимость вероятности ошибки, возникающей при передаче одиночного сигнала, будем писать Pe (E / N0 ) вместо Pe . Тогда, исходя из формул (34.3) и (34.4), можно записать выражение, связывающее вероятность ошибки на бит с отношением сигнал/шум на бит и включающее в себя параметры кода
|
m 1 |
|
d |
n |
|
Pe (bit ) + |
2 |
|
|
)Cni Pe 2(E / N0 )bit R log 2 q3i (1 Pe 2(E / N0 )bit R log2 q3)n i . (34.5) |
|
m |
|
|
|||
|
2 |
1 n i#t 1 |
|||
Рассмотрим примеры вычислений по формуле (34.5). Примеры соответствуют двоичным кодам БЧХ и передаче с использованием двоичных
противоположных сигналов: 1) q # 2 , n # 63 , k # 30 , |
d # 13 и 2) q # 2 , n # 63 , |
|
k # 57 , d # 3 . Графики вероятности |
ошибки на |
бит в зависимости от |
отношения сигнал/шум на бит показаны |
на рис.34.2 |
|
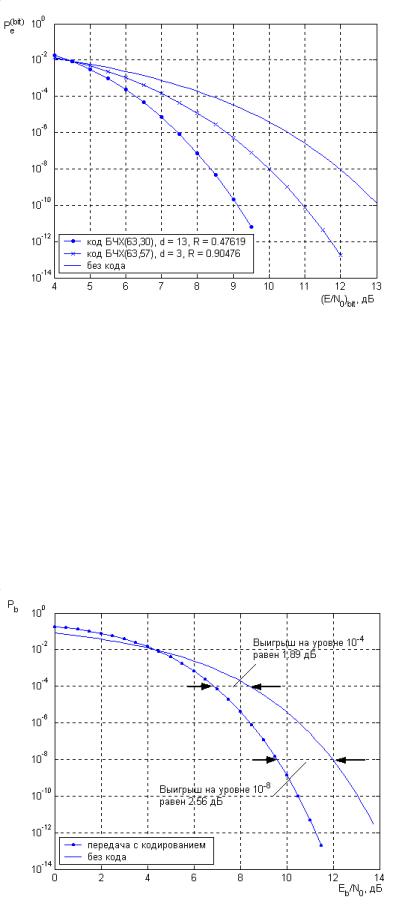
Рис.34.2 Вероятность ошибки на бит для двух кодов БЧХ и для передачи без кодирования
Эффективность применения кодирования может быть оценена количественно с использованием понятия энергетического выигрыша. Энергетический выигрыш обычно определяется из сравнения графиков, показывающих зависимость вероятности ошибки на бит от отношения сигнал/шум на бит для системы без кодирования и с кодированием. Энергетический выигрыш от кодирования определяется для некоторого
Рис.34.3 Определение энергетического выигрыша от кодирования по графикам
фиксированного уровня вероятности ошибки на бит как разница в отношении сигнал/шум на бит, требуемом для достижения этого значения вероятности ошибки при передаче с кодированием и без кодирования (см. рис. 34.3)
Из графиков, показанных на рис.34.3, видно, что величина выигрыша от кодирования может принимать различные значения. Более того она может быть отрицательной, например для этого примера при Eb / N0 4 4 дБ кодирование ухудшает вероятность ошибки и выигрыш становится отрицательным, т.е. становится проигрышем.
Вернемся к рассмотрению конкретного примера (рис.34.2) Пусть вероятность ошибки на бит фиксирована, например, на уровне 10 6 . Из графиков видно, что для достижения этой вероятности ошибки при передаче без кодирования требуется обеспечить отношение сигнал/шум на бит около 10.5 дБ. При использовании кода (63,57) требуется менее 9 дБ. Это значит, что код (63,57) обеспечивает энергетический выигрыш равный 10.5 9 # 1.5 дБ при вероятности ошибки на бит 10 6 . Если зафиксировать вероятность ошибки на
бит |
на уровне 10 8 , то |
выигрыш для |
этого кода |
составит величину |
||
12 10 # 2 дБ. |
Для кода |
(63,30) |
выигрыш |
составляет |
10.5 7.5 # 3 дБ при |
|
P (bit ) |
# 10 6 и |
12 8.4 # 3.6 дБ при |
P (bit ) # 10 8 . Видно, |
что а) разные коды |
||
e |
|
|
|
e |
|
|
имеют различные значения энергетического выигрыша от кодирования, б) выигрыш увеличивается с ростом отношения сигнал/шум.
Качество кода может быть оценено асимптотическим значением
энергетического выигрыша при |
2E / N0 3bit 6 5 . Асимптотический |
выигрыш |
||||||||
можно определить аналитически из формулы (34.5). |
Для двоичного кода эта |
|||||||||
формула приобретает вид |
|
|
|
|
|
|
|
|||
|
|
d |
n |
|
|
|
|
|
|
|
Pe |
(bit ) + |
)Cni Pe 2(E / N0 )bit R3i (1 Pe 2(E / N0 )bit R3)n i |
|
|||||||
|
|
|||||||||
|
|
n i#t 1 |
|
|
|
|
|
|
|
|
и при 2E / N0 3bit |
6 5 |
|
|
|
|
|
|
|
|
|
|
|
|
P (bit ) |
+ KP 2(E / N |
0 |
) |
bit |
R3t 1 , |
(34.6) |
|
|
|
|
e |
e |
|
|
|
|
||
где K # (d / n)Cnt 1 . Вероятность ошибки |
|
|
при |
использовании |
двоичных |
|||||
противоположных сигналов имеет вид |
|
|
|
|
|
|
||||

|
|
|
|
|
1 |
1 |
|
|
E |
. |
|
Pe (E / N |
0 ) # Q( |
2E / N |
0 ) 4 |
/ |
|
|
, |
||||
2 |
exp/ |
N0 |
, . |
||||||||
|
|
|
|
|
0 |
|
− |
||||
Используя неравенство (34.7) в (34.6) получаем, что |
|
|
|
|
|||||||
|
|
|
1 |
|
|
/ |
|
E |
, |
. |
|
(bit ) |
|
(t 1) / |
|
|
|
, |
|||||
|
|
|
1 |
|
. |
||||||
Pe |
+ K 2 |
|
exp/ |
R(t 1)/ |
|
|
|
, |
, . |
||
|
|
|
|
||||||||
|
|
|
0 |
|
|
0 N0 |
|
−bit − |
|||
При двоичной передаче без кодирования (E / N0 )bit # E / N0 и
(bit ) |
|
1 |
1 |
1 |
. . |
|||
# Pe # Q( 2(E / N0 )bit ) 4 |
/ |
/ |
E |
|
, |
, |
||
Pe |
2 |
exp/ |
/ |
N0 |
, |
, . |
||
|
|
0 |
0 |
−bit − |
||||
(34.7)
(34.8)
(34.9)
Сравнивая показатели экспонент в (34.7) и (34.9) нетрудно видеть, что они отличаются множителем R(t 1) , который и определяет скорость экспоненциального убывания вероятности ошибки с ростом отношения сигнал/шум. Поэтому асимптотический энергетический выигрыш, обозначаемый как G , составляет величину G # R(t 1) , или в децибелах
GдБ # 10 lg R(t 1) , дБ.
Легко подсчитать, что для рассмотренных примеров кодов (63,57) и (63, 30) асимптотический выигрыш составляет 2.58 дБ и 5.23 дБ соответственно. Заметим, что при конечных значениях отношения сигнал/шум энергетический выигрыш меньше своего асимптотического значения, но стремится к нему с ростом отношения сигнал/шум.

Приложение 0
Метол ортогонализации Грама – Шмидта
Метод ортогонализации Грама – Шмидта позволяет строить ортогональный базис по множеству функции (сигналов). Пусть имеется множество сигналов {si (t)} ,
i = 0,1,..., q −1. Требуется |
построить множество ортонормированных |
функций |
||||||||
(базис){ϕj (t)}, j =1,2,..., D . |
Не теряя общности, можно считать, что |
|
|
|
si (t) |
|
|
|
≠ 0 |
для всех i . |
|
|
|
|
|||||||
Это условие означает, что среди сигналов нет тождественно равных нулю. |
Построение |
|||||||||
базиса можно описать в виде алгоритма. Исходными данными для этого алгоритма служат
сигналы s0 (t),..., sq−1 (t) , |
а в результате формируется множество ортонормированных |
функций (базис) {ϕ j (t)}, |
j =1,2,..., D , D ≤ q . Алгоритм построение ортонормированного |
базиса представлен ниже. |
|
ϕ1 (t) ← s0 (t) /
 s0 (t)
s0 (t)
 ; D ←1;
; D ←1;
for i =1,2,..., q −1
ψ (t) ← si (t) −∑D (si (t),ϕj (t))ϕj (t);
j=1
if ψ (t)
 ≠ 0
≠ 0
D← D +1;
ϕD (t) ←ψ(t) / ψ (t)
 ;
;
end end
Поясним этот алгоритм. В качестве первой базисной функции выбирается любой сигнал, например, s0 (t) , деленный на норму этого сигнала. Этим достигается выполнение
условия |
|
|
|
ϕ1 (t) |
|
|
|
=1. Далее в цикле последовательно рассматриваются остальные сигналы и |
|
|
|
|
|||||
формируются |
|
|
|
базисные функции. Для этого вычисляется вспомогательная функция |
||||
ψ (t) как разность очередного сигнала и его разложения по построенным к этому моменту базисным функциям. Если функция ψ (t) не равна тождественно нулю, то очередная базисная функция вычисляется как ψ (t) / ψ (t)
 . Процесс оканчивается, если исследованы все сигнальные функции. В результате выполнения алгоритма формируется D ≤ q базисных функций. Равенство D = q выполняется только в случае, если все сигналы из множества {si (t)} , i = 0,1,..., q −1, оказываются линейно независимыми. Очевидно, что все построенные таким образом функции ϕj (t) , j =1,2,..., D , D ≤ q , будут нормированными.
. Процесс оканчивается, если исследованы все сигнальные функции. В результате выполнения алгоритма формируется D ≤ q базисных функций. Равенство D = q выполняется только в случае, если все сигналы из множества {si (t)} , i = 0,1,..., q −1, оказываются линейно независимыми. Очевидно, что все построенные таким образом функции ϕj (t) , j =1,2,..., D , D ≤ q , будут нормированными.
Нетрудно показать, что они при этом будут ортогональными.
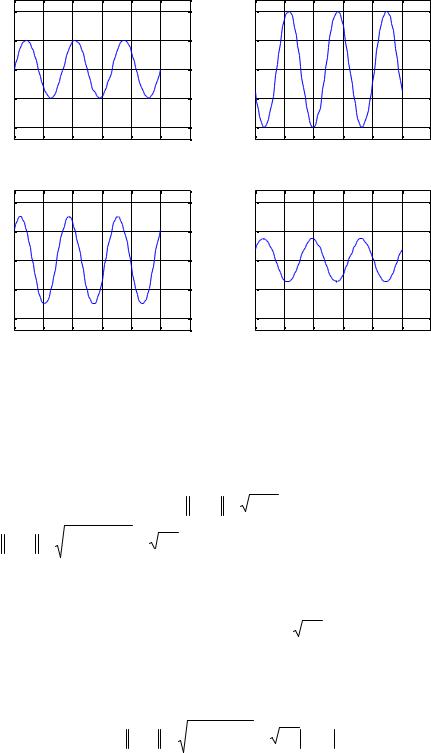
Рассмотрим пример. Пусть сигнальное множество содержит следующие четыре функции, заданные на интервале [0,T ] ,
s0 (t) = 2sin(2π(3/T )) , s1 (t) = −4 cos(2π(3 / T ) −θ) ,
|
|
|
|
|
s2 (t) = −3cos(2π(3 / T ) +π / 4) , |
|
|
|
||||
|
|
|
|
s3 (t) = −(3/ 2) cos(2π(3/T ) −5π / 6) , |
|
|
|
|||||
где θ и T – |
параметры. Графики этих сигналов показаны на рис.П.0.1 |
для значений |
||||||||||
T =1 и θ = 3π / 8 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s0(t) |
|
|
|
|
|
s1(t) |
|
|
|
4 |
|
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
-2 |
|
|
|
|
|
-2 |
|
|
|
|
|
|
-4 |
|
|
|
|
|
-4 |
|
|
|
|
|
|
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
|
|
|
s2(t) |
|
|
|
|
|
s3(t) |
|
|
|
4 |
|
|
|
|
|
2 |
|
|
|
|
|
0 |
|
|
|
|
|
-2 |
|
|
|
|
|
-4 |
|
|
|
|
|
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
4 |
|
|
|
|
|
2 |
|
|
|
|
|
0 |
|
|
|
|
|
-2 |
|
|
|
|
|
-4 |
|
|
|
|
|
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
Рис.П.0.1. Графики сигнальных функций s0 (t), s1 (t), s2 (t), s3 (t) . |
|
||||||||||
Последовательно выполняя шаги алгоритма, получаем: |
|
|||||||||||
1. Выражение для функции ϕ1 (t) имеет вид |
|
|||||||||||
|
|
ϕ1 (t) = s0 (t) / s0 (t) = 2 /T sin(2π(3/T )t) , |
(П.0.1) |
|||||||||
поскольку |
s0 (t) |
= ∫0T s0 (t)2 dt = |
2T . |
|
||||||||
2. |
Далее, |
применяя тождествоcos(a −b) = cos a cosb +sin a sin b к выражению для |
||||||||||
сигнала s1 (t) , легко вычисляем, что |
|
|
|
|
|
|||||||
|
|
(s1 ,ϕ1 ) = ∫0T s1 (t)ϕ1 (t)dt = −2 2T sinθ . |
|
|||||||||
Отсюда следует, что разностная функция на этом шаге алгоритма равна |
|
|||||||||||
|
ψ (t) = s1 (t) −(s1 ,ϕ1 )ϕ1 (t) = −4 cos(2π(3 / T )t −θ) + 4sinθ sin(2π(3 / T )t) . |
|||||||||||
Нетрудно |
вычислить, что ψ (t) |
= |
|
|
|
∫0Tψ (t)2 dt = 6T cosθ . Далее будем |
считать, что |
|||||
θ = 3π / 8 . Отсюда следует, что |
|
|
|
ψ (t) |
|
|
|
≠ 0 , и поэтому |
|
|||
|
|
|
|
|
||||||||
ϕ2 (t) =ψ (t) / |
|
|
|
ψ (t) |
|
|
|
= |
4(−cos(2π(3/T )t −3π / 8) +sin(3π / 8)sin(2π(3/ T )t)). |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2T cos3π / 8 |
3. Рассмотрим функцию s2 (t) и определим вид функции ψ (t) алгоритма. Функция ψ (t) для этого шага алгоритма определяется как
ψ (t) = s2 (t) −(s2 ,ϕ1 )ϕ1 (t) −(s2 ,ϕ2 )ϕ2 (t) .
(П.0.2)
на этом шаге
(П.0.3)
Используя выражения (П.0.1) и (П.0.2), |
после некоторых по |
сути несложных, но |
|
громоздких преобразований получаем, |
что |
(s2 ,ϕ1 ) =3 T / 2 |
и (s2 ,ϕ2 ) = −3 T / 2 . |
Подстановка этих значений в (П.0.3) в итоге приводит к равенству ψ (t) = 0 . Это равенство означает, что рассмотрение функции s2 (t) не влечет увеличения числа базисных функций.
4. Осталось рассмотреть последнюю сигнальную функцию s3 (t) . Разностная функция в этом случае равна ψ (t) = s3 (t) −(s3 ,ϕ1 )ϕ1 (t) −(s3 ,ϕ2 )ϕ2 (t) . Здесь после вычислений получаем, что (s3 ,ϕ1 ) = 3 6T / 8 и (s3 ,ϕ2 ) = −3
6T / 8 и (s3 ,ϕ2 ) = −3 2T / 8 , и в итоге вновь оказывается, что ψ(t) = 0 . Выполнение алгоритма на этом шаге заканчивается.
2T / 8 , и в итоге вновь оказывается, что ψ(t) = 0 . Выполнение алгоритма на этом шаге заканчивается.
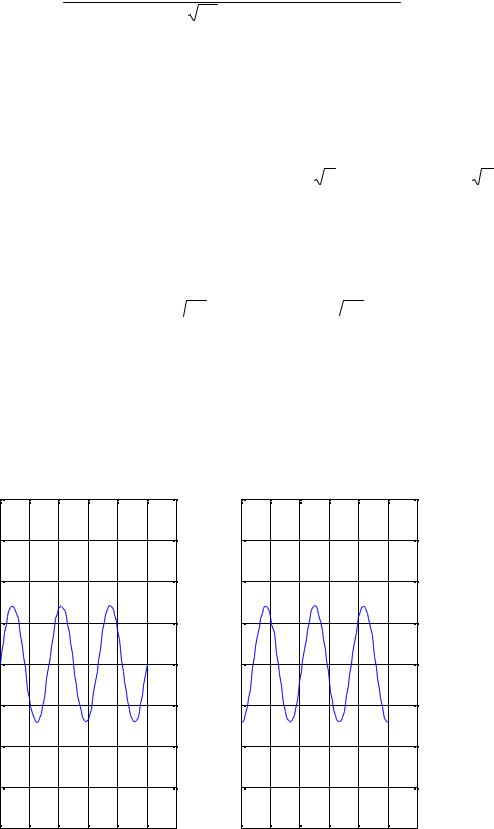
Рассмотрев, таким образом сигнальные функции s0 (t) , s1 (t) , s2 (t) и s3 (t) , получаем, для их представления достаточно иметь две базисные функции ϕ1 (t) и ϕ1 (t) , заданные равенствами (П.0.1) и (П.0.2) соответственно. Графики базисных функций показаны на рис.П.0.2.
4 |
|
|
φ1(t) |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
|
|
-1 |
|
|
|
|
|
-2 |
|
|
|
|
|
-3 |
|
|
|
|
|
-40 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
4 |
|
|
φ2(t) |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
|
|
-1 |
|
|
|
|
|
-2 |
|
|
|
|
|
-3 |
|
|
|
|
|
-40 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
Рис.П.0.2. Графики ортонормированных базисных функций ϕ1 (t),ϕ2 (t) .
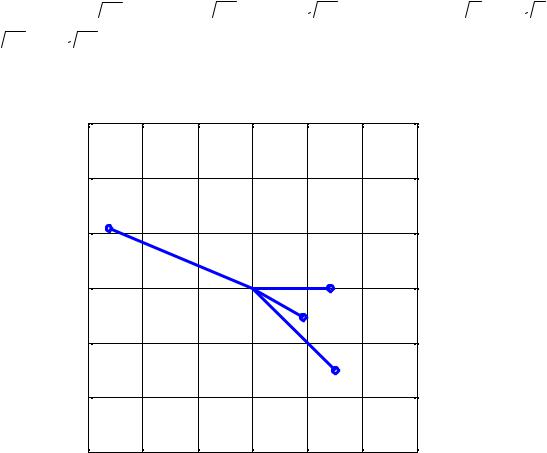
Координаты сигнальных точек, соответствующие сигналам s0 (t) , s1 (t) , s2 (t) и s3 (t) , равны s0 = ( 2T ,0) , s1 = (−2
2T ,0) , s1 = (−2 2T sin 3π / 8, 2
2T sin 3π / 8, 2  2T cos3π / 8) , s2 = (3
2T cos3π / 8) , s2 = (3 T / 2, −3
T / 2, −3  T / 2) , s3 = (3
T / 2) , s3 = (3 6T / 8, −3
6T / 8, −3  2T / 8) . Множество сигнальных точек (сигнальное созвездие) для этих функций, полученное с использованием построенного базиса, показано на рис. П.0.3.
2T / 8) . Множество сигнальных точек (сигнальное созвездие) для этих функций, полученное с использованием построенного базиса, показано на рис. П.0.3.
3 
2 |
|
|
|
|
|
|
|
s1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
s0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
s3 |
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
s2 |
|
-2 |
|
|
|
|
|
|
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
-3 |
Рис.П.0.3. Множество сигнальных точек s0 , s1 , s2 , s3 . .

Приложение 1
Сигналы с непрямоугольными огибающими
Двумерные сигнала, в частности сигналы КАМ и ФМ, представимы в виде
|
|
si (t) = si1ϕ1 (t) + si 2ϕ2 (t) , |
|
|
(П.1.1) |
||||
где ϕ1 (t) , ϕ2 (t) – ортонормированные |
функции, si1 , si 2 – коэффициенты, |
задающие |
|||||||
конкретный сигнал. В частности, если |
|
|
|
|
|
|
|
||
ϕ (t) = |
2 cos 2πf |
t , ϕ |
2 |
(t) = |
2 sin 2πf |
t , 0 <t <T , |
|
||
1 |
T |
0 |
|
|
T |
0 |
|
|
|
|
|
|
|
|
|
|
|
||
то сигнал si (t) имеет вид отрезка гармонической функции длительности T с постоянной амплитудой.
В общем случае функцииϕ1 (t) иϕ2 (t) |
могут быть заданы как ϕ1 (t) = m(t) cos 2πf0t , |
|||||
ϕ2 (t) = m(t)sin 2πf0t , где |
m(t) – огибающая, |
выбранная таким образом, что ϕ1 (t) иϕ2 (t) |
||||
образуют ортонормированный базис, −∞ < t < ∞ . |
Пусть M ( f ) ↔ m(t) , тогда спектр |
|||||
сигнала si (t) равен |
|
|
|
|
||
Si ( f ) = |
si1 |
|
(M ( f − f0 ) + M ( f + f |
0 ))+ |
si 2 |
(M ( f − f0 ) − M ( f + f0 )). |
|
2 j |
|||||
2 |
|
|
|
|
||
Очевидно, что спектр сигнала сосредоточен около несущей частоты f0 , а его форма и ширина полосы частот определяются видом функции M ( f ) однозначно определяемой огибающей m(t) . Выбор огибающей m(t) в виде кусочно–постоянной функции на интервале [0,T ] приводит к спектру вида sin x / x . Ширина полосы частот при этом равна
W = 2 /T .
При другом выборе огибающей возможно сокращение полосы до величины 1/T . В частности, это достигается путем применения огибающей вида sin x / x . В последующем рассмотрении используется функция sinc(x), которая связана с функцией sin x / x .
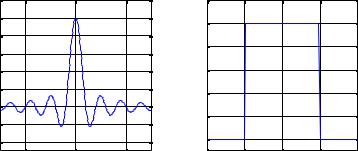
Функция sinc(x) определена как
sinc(x) = sinπxπx .
Определим также функцию прямоугольного импульса
1, x ≤1/ 2 rect(x) =
0,впротивномслучае
Графики этих функций показаны на рис. П.1.1
|
1.2 |
|
|
|
1 |
|
|
|
0.8 |
|
|
sinc(x) |
0.6 |
|
rect(x) |
0.4 |
|
||
|
|
|
|
|
0.2 |
|
|
|
0 |
|
|
|
-0.2 |
|
|
|
-0.4 |
|
|
|
-5 |
0 |
5 |
|
|
x |
|
1.2 |
|
|
|
|
1 |
|
|
|
|
0.8 |
|
|
|
|
0.6 |
|
|
|
|
0.4 |
|
|
|
|
0.2 |
|
|
|
|
0 |
|
|
|
|
-1 |
-0.5 |
0 |
0.5 |
1 |
|
|
x |
|
|
|
|
Рис. П.1.1. Графики функций sinc(x) и rect(x) . |
|
||||||||||
Рассмотрим некоторые свойства этих функций. |
|
|
|
|
|
|
|
||||||
1. |
Четность функций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sinc(x) = sinc(−x) , rect(x) = rect(−x) . |
|
||||||||||
2. |
Частные значения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sinc(0) =1, sinc(k) = 0 для k = ±1,±2,±3,... |
|
||||||||||
3. |
Преобразование Фурье |
sinc(x) ↔ rect( y) . |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
Доказательство. |
Вычисляя |
обратное преобразование |
Фурье |
от функции rect( y) , |
|||||||||
получаем |
|
|
|
|
1/ 2 |
|
|
|
|
|
|
|
|
|
∞ |
1/ 2 |
|
j 2πxy |
|
|
jπx |
−e |
− jπx |
1 |
|
|
|
|
|
|
|
|
|
||||||||
|
∫rect( y)e j 2πxy dy = ∫e j 2πxy dy = e |
|
|
|
= e |
|
|
= sin πx = sinc(x) . □ |
|||||
|
|
|
|
|
|
|
|
||||||
|
−∞ |
−1/ 2 |
j2πx |
|
−1/ 2 |
|
2 j |
|
πx |
πx |
|||
|
|
|
|
|
|
|
|
|
|||||
4. |
Произведение двух rect( ) функций |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
rect(x) rect(x) = rect(x) . |
|
|
|
|||||||
5. |
Свертка двух sinc( ) функций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sinc(x) sinc(x) = sinc(x) . |
|
|
|
|||||||
Доказательство. |
Обозначим ψ (x) = sinc(x) sinc(x) . |
Пусть Ψ( y) |
преобразование Фурье |
||||||||||
функции ψ ( y) , то есть ψ( y) ↔ Ψ( y) . По определению |
|
|
|
|
|||||||||
ψ(x) = ∞∫sinc(x1 )sinc(x − x1 )dx1 .
−∞
Используя теорему о свертке для преобразования Фурье и свойства 3 и 4, получаем
Ψ( y) = rect( y) rect( y) = rect( y).
Поскольку ψ( y) ↔ Ψ( y) и sinc(x) ↔ rect( y) , то ψ(x) = sinc(x) . □
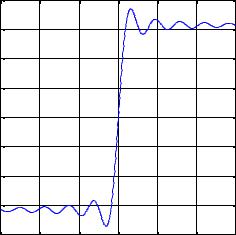
6. Автокорреляция функции sinc(x)
∞∫sinc(x)sinc(x − x1 )dx = sinc(x1 ) .
−∞
Доказательство. Используя четность функции sinc( ) и свойство 5, получаем требуемое утверждение. □
7. Функции |
ϕk (x) = sinc(x −k) , |
k – целое, образуют ортонормированный базис на |
интервале (−∞,+∞) , то есть |
|
|
|
|
∞∫ϕk (x)ϕl (x)dx =δkl . |
Доказательство. |
−∞ |
|
|
||
∞∫ϕk (x)ϕl (x)dx = ∞∫sinc(x −k)sinc(x −l)dx = ∞∫sinc(x)sinc(x +k −l)dx = sinc(l −k) =δkl . □ |
||
−∞ |
−∞ |
−∞ |
8. Связь с функцией интегрального синуса Si( ) .
Функция интегрального синуса определена как Si(t) = ∫0t sin x / xdx . График функции Si( ) показан на рис. П.1.2.
|
2 |
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
Si(x) |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0.5 |
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
-1.5 |
|
|
|
|
|
|
|
-2 |
-20 |
-10 |
0 |
10 |
20 |
30 |
|
-30 |
||||||
|
|
|
|
x |
|
|
|
|
|
Рис.П.1.2. График функции Si(x) |
|||||
Выполняются равенства
Доказательство.
t
∫sinc(x)dx
0
|
∫t |
sinc(x)dx = |
1 |
Si(πt) , |
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||||
|
0 |
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sinc(t) = |
d |
|
|
1 |
|
Si(πt) . |
|
|
|
|||||||
|
dt π |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
t |
|
|
πx = y |
|
|
|
|
|
|
|
|
1 |
πt |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= ∫sin πx dx = |
x =π −1 y |
|
|
= |
∫sin y dy = |
Si(πt) . □ |
|||||||||||
|
|
|
|
||||||||||||||
0 |
πx |
|
dx =π |
−1dy |
|
π |
0 |
y |
π |
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
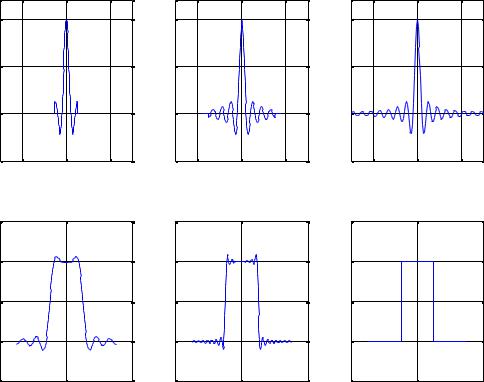
9. Спектр отрезка функции sinc(x) .
Пусть
s(t) = sinc(t), | t |<Ts / 2,0,| t |≥Ts / 2 .
Этот сигнал представляет собой отрезок функции sinc( ) длительности Ts . Найдем
спектр этой функции S( f ) ↔ s(t) . Легко заметить, что s(t) = sinc(t) rect(t /Ts ) , −∞ < t < ∞ . Тогда используя теорему о свертке и учитывая, что
rect(t / Ts ) ↔Ts sinc( fTs ) , sinc(t) ↔ rect( f ) ,
получаем, что
|
|
|
|
∞ |
|
|
f +1/ 2 |
|
S( f ) = rect( f ) Ts sinc( fTs ) =Ts ∫sinc(xTs ) rect( f − x)dx =Ts |
∫sinc(xTs )dx = |
|
||||||
|
|
|
|
−∞ |
|
|
f −1/ 2 |
|
= |
|
y = xTs |
|
(f +1/ 2)T |
1 (Si(f +1/ 2)πTs −Si(f −1/ 2)πTs ). |
(П.1.2) |
||
|
|
|||||||
|
dy =Ts dx |
|
= ∫sinc( y)dy = |
|||||
|
|
|
|
s |
|
|
|
|
|
|
dx = (1/ Ts )dy |
|
(f −1/ 2)Ts |
π |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Здесь в последнем переходе использовано свойство 8. Графики функций s(t) и S( f ) для различных значений Ts показаны на рис. П.1.3. Видно, что ростом значения Ts форма спектра приближается к прямоугольной, и в пределе спектр равен rect( f ) . □
|
|
Ts = 5 |
|
|
|
Ts = 15 |
|
|
|
Ts = ∞ |
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
s(t) |
0.5 |
|
|
s(t) |
0.5 |
|
|
s(t) |
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
|
|
|
0 |
|
|
|
0 |
|
|
|
-0.5 |
0 |
10 |
|
-0.5 |
0 |
10 |
-0.5 |
0 |
10 |
|
|
-10 |
|
-10 |
|
-10 |
||||||
|
|
t |
|
|
|
t |
|
|
|
t |
|
|
1.5 |
|
|
|
1.5 |
|
|
|
1.5 |
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
S(f) |
0.5 |
|
|
S(f) |
0.5 |
|
|
S(f) |
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
|
|
|
0 |
|
|
|
0 |
|
|
|
-0.5 |
0 |
2 |
|
-0.5 |
0 |
|
-0.5 |
0 |
2 |
|
|
-2 |
|
-2 |
|
2 |
-2 |
|||||
|
|
f |
|
|
|
f |
|
|
|
f |
|
|
|
|
Рис. П.1.3. Графики функций s(t) |
и S( f ) |
|
|
|||||
Для формирования сигналов, si (t) , определенных равенством (П.1.1) следующих с периодом T и занимающих полосу W =1/T , выберем функции ϕ1 (t) и ϕ2 (t) следующим образом
ϕ1 (t) = |
2W sinc(Wt) cos 2πf0t , |
(П.1.3) |
ϕ2 (t) = |
2W sinc(Wt)sin 2πf0t , |
(П.1.4) |
где −∞ < t < ∞ , f0 >W / 2 . Покажем, что ϕ1 (t) и ϕ2 (t) |
образуют ортонормированный |
|
базис
1.Ортогональность. Поскольку ϕ1 (t) – четная функция, а ϕ2 (t) – нечетная, то их произведениеϕ1 (t)ϕ2 (t) – нечетная функция. Следовательно, ∫−∞∞ϕ1 (t)ϕ2 (t)dt = 0 . □
2.Норма. Пусть Φ1 ( f ) ↔ϕ1 (t) . Найдем выражение для Φ1 ( f ) . Поскольку sinc(Wt) ↔W −1 rect( f /W ) , то
Φ |
|
( f ) = |
1 |
|
2WW |
− |
|
|
f − |
|
f |
0 |
|
|
|
|
|
|
|
|
|
− |
|
|
f |
+ f |
0 |
|
|
||||||||||||||||||
|
|
|
|
1 rect |
|
|
|
|
|
|
|
+ |
|
|
2WW |
1 rect |
|
= |
|||||||||||||||||||||||||||||
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
1 |
|
|
|
|
|
f − f |
|
|
|
|
|
|
|
|
|
f + f |
|
|
|
|
|
|
|
(П.1.5) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rect |
|
|
|
|
0 |
+rect |
|
|
|
|
0 . |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2W |
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Учитывая, что f0 |
>W / 2 и rect(x)2 = rect(x) , |
|
получаем, что |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
f |
|
− |
|
f |
|
|
|
|
|
|
f |
+ |
f |
|
|
|
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
Φ |
( f ) |
|
|
|
= |
|
|
|
|
rect |
|
|
|
|
|
|
|
|
|
|
+ rect |
|
|
|
|
|
|
|
, |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2W |
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
||||||||
откуда следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
∞∫ϕ1 (t)2 dt = ∞∫ |
|
Φ1 ( f ) |
|
2 df =1. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для Φ2 ( f ) ↔ϕ2 (t) |
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Φ |
|
( f ) = |
|
1 |
|
|
|
|
|
|
|
|
− |
|
|
f − f |
|
|
|
|
− |
|
|
|
|
|
|
− |
|
|
|
f + f |
0 |
|
= |
||||||||||||
2 |
|
|
|
|
|
2WW 1 rect |
|
|
|
|
|
|
|
0 |
|
|
|
2WW 1 rect |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|||||
|
|
|
|
|
2 j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
= − j |
|
1 |
|
|
|
|
|
f − f |
0 |
|
|
|
|
|
|
|
|
|
f |
+ f |
0 |
|
, |
|
|
|
|
|
|
(П.1.6) |
||||||||||||||
|
|
|
|
|
|
|
|
rect |
|
|
|
|
|
−rect |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
2W |
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
f |
|
− |
|
f |
|
|
|
|
|
|
f |
+ |
f |
|
|
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
Φ |
|
( f ) |
|
|
|
= |
|
|
|
rect |
|
|
|
|
|
|
|
|
|
+ rect |
|
|
|
|
|
. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Следовательно
∞∫ϕ2 (t)2 dt = ∞∫Φ2 ( f ) 2 df =1.
−∞ −∞
□
Поскольку, функции ϕ1 (t) и ϕ2 (t) имеют бесконечную длительность, то при
передаче сигналов вида (П.1.1) с периодом следования T =1/W , неизбежно их перекрытие, иначе говоря, возможна межсимвольная интерференция. Для того, чтобы исключить влияния перекрытия сигналов во временной области должны выполняться условия ортогональности сдвигов функций ϕ1 (t) и ϕ2 (t) . Это значит, что для целых
ненулевых |
|
k должны |
выполняться |
|
условия: |
|
|
1) |
|
∫−∞∞ϕ1 (t)ϕ1 (t −k /W )dt = 0 , |
|||||||||||||||||||||||
2) ∫−∞∞ϕ2 (t)ϕ2 (t −k /W )dt = 0 , |
3) |
|
∫−∞∞ϕ1 (t)ϕ2 (t −k /W )dt = 0 . Докажем |
выполнение |
этих |
||||||||||||||||||||||||||||
условий. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство условия 1. |
Обозначим свертку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
ψ11 (t) = ∞∫ϕ1 (x)ϕ1 (t − x)dx . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть Ψ11 ( f ) – преобразование Фурье функции ψ11 (t) . По теореме о свертке |
|
|
|
||||||||||||||||||||||||||||||
Ψ |
( f ) = Φ |
( f |
|
1 |
f − f |
|
|
|
|
f |
+ |
f |
|
|
2 |
= |
|
1 |
|
f − |
f |
|
|
f + |
f |
|
|
||||||
)2 = |
rect |
|
|
0 |
|
+ rect |
|
|
|
|
0 |
|
|
|
|
rect |
|
0 |
|
+ rect |
|
0 |
|
||||||||||
11 |
1 |
|
|
|
|
W |
|
|
W |
|
|
|
|
|
|
2W |
|
W |
|
|
|
W |
|
|
|
||||||||
|
|
|
|
2W |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Поскольку ψ11 (t) ↔ Ψ11 ( f ) и учитывая, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
f − f |
0 |
|
|
↔We |
j 2πf |
0 sinc(Wt) , |
|
|
|
|
|
|
(П.1.7) |
|||||||||||||
|
|
|
|
rect |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
f + |
f |
0 |
|
|
↔We |
− j 2πf |
|
|
sinc(Wt) |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
rect |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
(П.1.8) |
||||||||||||
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
получаем, что
ψ11 (t) = 2W1 (We j 2πf0t sinc(Wt) +We− j 2πf0t sinc(Wt))= sinc(Wt) cos 2πf0t .
Всилу четности функции ϕ1 (t) имеем
∞∫ϕ1 (t)ϕ1 (t −k /W )dt = ∞∫ϕ1 (t)ϕ1 (k /W −t)dt =ψ11 (kW ) = sinc(k) cos(2πf0 k /W ) = 0 . □
−∞ −∞
Доказательство условия 2. Поступая аналогично предыдущему пункту, обозначим свертку
ψ22 (t) = ∞∫ϕ2 (x)ϕ2 (t − x)dx .
−∞
Пусть Ψ22 ( f ) – преобразование Фурье функции ψ22 (t) . По теореме о свертке
Ψ ( f ) |
= Φ |
|
( f )2 |
|
− j |
1 |
|
|
f − f |
0 |
|
f + f |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
= |
|
rect |
|
|
−rect |
0 |
= |
|
|
|
|
|
|
|
|
|
|
|
|||||||
22 |
|
|
|
|
2W |
|
|
W |
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
f − f |
0 |
|
f + |
f |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
|
|
rect |
|
|
+ rect |
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2W |
|
|
W |
|
|
W |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Далее, принимая во внимание нечетность функции ϕ2 (t) |
|
и используя равенства (П.1.7) и |
||||||||||||||||||||||||
(П.1.8), |
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∞∫ϕ2 (t)ϕ2 (t −k /W )dt = − ∞∫ϕ2 (t)ϕ2 (k /W −t)dt = −ψ22 (kW ) = sinc(k) cos(2πf0 k /W ) = 0 . |
□ |
|
||||||||||||||||||||||||
−∞ |
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Доказательство условия 3. Пусть
ψ12 (t) = ∞∫ϕ1 (x)ϕ2 (t − x)dx
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и Ψ12 ( f ) |
– преобразование Фурье функции ψ12 (t) . По теореме о свертке |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Ψ12 ( f ) = Φ1 ( f )Φ2 ( f ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
− j |
1 |
|
f − f |
|
|
f + f |
|
|
1 |
f − f |
|
|
f |
+ |
f |
|
|
= |
|
|
|
||||
= |
|
rect |
0 |
−rect |
|
0 |
|
rect |
0 + rect |
|
|
|
0 |
|
|
|
|
|||||||||
|
|
2W |
W |
W |
|
|
2W |
W |
|
|
|
W |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
= − j |
1 |
|
f − |
f |
0 |
|
|
|
|
f |
+ |
f |
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
rect |
|
|
|
−rect |
|
|
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
W |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2W |
|
|
|
|
|
|
|
|
|
|
|
||||
Применяя обратное преобразование Фурье к функции Ψ12 ( f ) , получаем с использованием равенств (П.1.7) и (П.1.8), что
ψ12 (t) = − j |
1 |
(We j 2πf0 sinc(Wt) −We− j 2πf0 |
sinc(Wt))= sinc(Wt) sin 2πf0t , |
|
|||
и тогда |
2W |
|
|
|
|
|
|
∞∫ϕ1 (t)ϕ2 (t −k /W )dt = − ∞∫ϕ1 (t)ϕ2 (k /W −t)dt = −ψ12 (k /W ) = 0 . □ |
|||
−∞ |
|
−∞ |
|
Итак, получено, что сигналы вида (П.1.1), |
где базисные функции ϕ1 (t) и ϕ2 (t) , |
||
определены равенствами (П.1.3) и (П.1.4), обладают следующими свойствами:
–спектр сигналов, как следует из выражений (П.1.5) и (П.1.6), строго прямоугольный, локализован, около частоты f0 и ширина его равна W .
–несмотря на то, что последовательно передаваемые сигналы перекрываются во времени (интерферируют), их влияние друг на друга в силу ортогональности сдвигов базисных функций отсутствует; минимальный временной сдвиг, при котором обеспечивается ортогональность, равен T =1/W ; величина T имеет смысл периода следования сигналов.
Поскольку на практике сигналы не могут иметь бесконечную длительность, то
оценим влияние конечной длительности базисных функций ϕ1 (t) и ϕ2 (t) . Для этого рассмотрим функции вида
Очевидно, что
ϕ~1 (t)
~ (t)
ϕ2
~ |
|
ϕ1 |
(t), −Ts / 2 < t <Ts / 2 |
, |
ϕ1 |
(t) = |
иначе |
||
|
|
0, |
|
|
~ |
|
ϕ2 |
(t), −Ts / 2 < t <Ts / 2 |
. |
ϕ2 |
(t) = |
иначе |
||
|
|
0, |
|
|
=rect(t /Ts ) 2W sinc(Wt) cos 2πf0t , −∞ < t < ∞ ,
2W sinc(Wt) cos 2πf0t , −∞ < t < ∞ ,
=rect(t / Ts ) 2W sinc(Wt)sin 2πf0t , −∞ < t < ∞ .
2W sinc(Wt)sin 2πf0t , −∞ < t < ∞ .
Пусть m(t) = |
2W rect(t /Ts )sinc(Wt) и M ( f ) |
– преобразование Фурье функции m(t) , |
|
M ( f ) ↔ m(t) . |
По аналогии с выводом равенства (П.1.2) имеем |
||
M ( f ) = |
2WTs sinc( fTs ) 1 rect( f /W ) = |
2 Ts |
∞∫sinc(xTs ) rect(( f − x) /W )dx = |
|
W |
W |
−∞ |
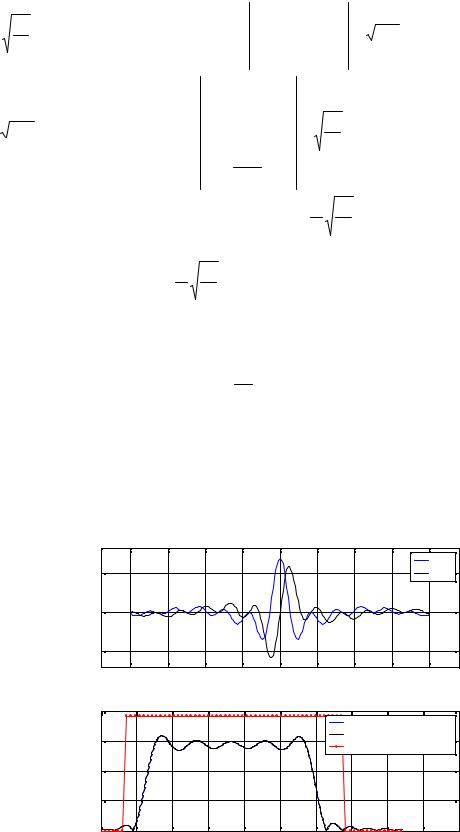
|
|
|
|
|
|
|
|
|
y = (x − f ) /W |
|
∞∫sinc((Wy + f )Ts ) rect(y)dy = |
||||||||
= |
2 |
Ts |
∞∫sinc(xTs ) rect((x − f ) /W )dx = x =Wy + f |
|
= |
2W Ts |
|||||||||||||
|
W |
−∞ |
|
|
|
|
|
dx =Wdy |
|
|
|
−∞ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1/ 2 |
|
|
u = (Wy + f )Ts |
2 |
( f +W / 2)Ts |
|
|
|
|
|
|
|||||
= |
2W Ts |
∫sinc((Wy + f )Ts )dy = du =WTs dy |
= |
∫sinc(u)du = |
|
|
|
|
|
||||||||||
|
|
|
−1/ 2 |
|
|
|
du |
|
W |
( f −W / 2)T |
|
|
|
|
|
|
|||
|
|
|
|
|
|
dy = |
|
|
|
s |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
WT |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1 |
|
2 (Si(( f +W / 2)πT )−Si(( f −W / 2)πT )). |
|||||||
|
|
|
|
|
|
|
|
|
|
π |
W |
|
|
s |
|
|
|
s |
|
То есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
M ( f ) = 1 |
2 (Si(( f +W / 2)πT ) |
−Si(( f −W / 2)πT )). |
|
|
(П.1.9) |
||||||||||
|
|
|
|
|
π |
W |
|
|
|
|
s |
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Используя свойства преобразования Фурье, получаем окончательно, что |
|
|
|
|
|||||||||||||||
|
|
|
|
|
~ |
|
1 |
(M ( f |
− f0 ) |
+ M ( f + f0 )), |
|
|
|
|
|
||||
|
|
|
|
|
Φ1 ( f ) = |
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
( f ) = |
1 |
|
(M ( f − f0 ) − M ( f + f0 )), |
|
|
|
|
|
|||||
|
|
|
|
|
Φ2 |
2 j |
|
|
|
|
|
||||||||
где функция M ( f ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
определена равенством (П.1.9). |
|
|
|
|
|
|
|
|
|||||||||||
|
|
Рассмотрим |
иллюстрирующий |
пример. |
Пусть |
несущая |
частота |
f0 |
=1800 |
Гц, |
|||||||||
модуляционная скорость Vмод = 2400 Бод, |
длительность сигнала |
Ts = |
0.004 |
с = 4 |
мс. |
||||||||||||||
|
|
|
|
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Графики функций ϕ1 (t) |
и ϕ2 (t) и их амплитудных спектров показаны на рис. П.1.4 |
|
|||||||||||||||||
|
|
|
|
|
f0 =1800 Hz, W = 2400 Hz, T = 1/W s,Ts = 0.004 s |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φ1(t) |
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
φ2(t) |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
-1.5 |
-1 |
-0.5 |
|
0 |
0.5 |
|
1 |
1.5 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t, s |
|
|
|
|
|
-3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 10 |
|
|
|
|
|
0.02 |
|
|
|Φ1(f)| |
0.015 |
|Φ2(f)| |
|
Channel band (300..3400 Hz) |
0.01
0.005
00 500 1000 1500 2000 2500 3000 3500 4000 4500 5000 f, Hz
Рис. П.1.4. Графики функций ϕ~1 (t) и ϕ~2 (t) и их амплитудных спектров
Приложение 2
О моделировании передачи сигналов заданных отсчетами во временной области
Пусть сигнал на выходе канала с АБГШ со спектральной плотностью мощности N0 / 2 задается выражением
|
r(t) = si (t) + n(t) , |
(П.2.1) |
|||||
где 0 < t <Ts , Ts – длительность сигнала, |
i = 0,1,..., q −1. Каждый сигнал si (t) может быть |
||||||
представлен как линейная комбинация базисных ортонормированных функций |
|
||||||
|
|
|
D |
|
|
|
|
si (t) = ∑sijϕj (t) , |
(П.2.2) |
||||||
|
|
|
j=1 |
|
|
|
|
где D – размерность сигнального пространства. Отношение сигнал/шум определяется как |
|||||||
|
E |
|
1 |
|
1 |
q −1 |
|
|
= |
|
∑Ei , |
(П.2.3) |
|||
|
|
N0 |
|
||||
|
N0 |
q i =0 |
|
||||
где Ei – энергия i -го сигнала.
Для моделирования во временной области передачи по каналу с шумом, заданному выражением (П.2.1), представим принятый сигнал в виде последовательности отсчетов, взятых с интервалом ∆t , то есть
|
|
|
|
|
|
|
|
r (l ) = si(l ) +n(l ) , |
(П.2.4) |
|||
где r (l ) = r(l∆t) , |
si(l ) = sl (l∆t) |
– отсчет сигнала на выходе канала и отсчет переданного |
||||||||||
сигнала соответственно, l =1,2,..., N |
s |
, ∆t =T / N |
s |
, а случайная величина n(l ) учитывает |
||||||||
|
|
|
|
|
|
|
s |
|
|
|
||
влияние шума. |
Для канала с АБГШ n(l ) представляет собой гауссовскую случайную |
|||||||||||
величину, и |
|
|
= 0 , |
(n(l ) )2 |
=σ 2 . При моделировании величин n(l ) |
требуется определить |
||||||
n(l ) |
|
|||||||||||
значение дисперсии |
отсчета |
σ 2 и |
|
связать |
его с отношением |
сигнал/шум (П.2.3). |
||||||
Рассмотрим получение этой зависимости.
Для дискретизированного сигнала можно указать разложение аналогичное равенству (П.2.2)
D |
D |
|
si(l ) = si (l∆t) = ∑sijϕj (l∆t) = ∑sijϕ(jl ) , |
(П.2.5) |
|
j=1 |
j=1 |
|
где ϕ(jl ) =ϕj (l∆t) – отсчет базисной функции. |
Выберем число отсчетов Ns |
так, чтобы с |
приемлемой точностью выполнялись условия |
|
|
N |
1, k = j |
|
∑ϕk(l )ϕ(jl ) ∆t ≈δkj = |
(П.2.6) |
|
l=1 |
0, k ≠ j |
|
для всех j, k =1,2,..., D . Энергия дискретизированного сигнала равна
Ei = ∑Ns (si(l ) )2 ∆t . l =1
C использованием равенств (П.2.5) и (П.2.6) несложно показать, что Ei = ∑Dj=1 sij2 .

Случайная величина n j , определенная как
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ts |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n j = ∫n(t)ϕj (t)dt |
|
|
|
||||||||||||||
где n(t) |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
– белый гауссовский процесс, имеет гауссовское распределение с параметрами |
||||||||||||||||||||||||||||||
|
|
= 0 и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
= (N0 / 2) |
|
|
|
ϕj (t) |
|
|
|
2 = (N0 / 2) . |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
n2j |
|
(П.2.7) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Для базисной функции, заданной отсчетами, имеем |
|
|
|
|
||||||||||||||||||||||||||
|
|
Ts |
|
N |
l∆t |
|
|
|
|
|
|
N |
l∆t |
|
|
|
|
|
|
|
|
N |
l∆t |
N |
||||||
|
n j = ∫n(t)ϕj (t)dt = ∑s |
∫n(t)ϕj (l∆t)dt = ∑s |
|
|
|
∫n(t)ϕ(jl ) dt = |
∑s ϕ(jl ) |
∫n(t)dt = ∑s ϕ(jl )ξ(l ) , (П.2.8) |
||||||||||||||||||||||
0 |
|
l=1 (l−1)∆t |
|
|
|
|
|
|
l=1 (l−1)∆t |
|
|
|
|
|
|
|
|
l=1 |
(l−1)∆t |
l=1 |
||||||||||
|
где ξ(l ) |
= ∫(ll∆−t1)∆t n(t)dt |
– гауссовская случайная величина с нулевым средним и дисперсией |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σξ2 |
= (N0 / 2)∆t . |
|
|
(П.2.9) |
||||||||||||
|
|
|
При достаточно большом числе отсчетов |
|
|
Ns , |
то есть при малой длительности |
|||||||||||||||||||||||
интервала ∆t дискретизации, с приемлемой точностью выполняется равенство |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Ts |
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
||||
|
|
|
|
|
|
|
|
n j |
= ∫n(t)ϕj (t)dt ≈ ∑s |
n(l )ϕj (l∆t)∆t , |
(П.2.10) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
l=1 |
|
|
|
|
|||
где n(l ) |
|
– гауссовские случайные величины, |
определенные в |
равенстве (П.2.4). Из |
||||||||||||||||||||||||||
равенств (П.2.7), (П.2.8), (П.2.9) и (П.2.10) следует, |
что |
n(l ) ∆t =ξ(l ) . Следовательно, |
||||||||||||||||||||||||||||
σ 2 = |
|
=σξ2 / ∆t 2 = (N0 / 2) / ∆t , откуда следует, |
|
|
||||||||||||||||||||||||||
(n(l ) )2 |
что |
N0 / 2 =σ 2 ∆t . Тогда из формулы |
||||||||||||||||||||||||||||
(П.2.3) получаем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
E |
|
|
|
1 |
|
q−1 |
|
|
|
|
|
1 |
|
|
q−1 |
Ns |
|
|
|||||
|
|
|
|
|
|
|
= |
|
|
|
1 ∑Ei = |
|
|
1 ∑∑(si(l ) )2 . |
|
|||||||||||||||
|
|
|
|
|
|
|
N0 |
|
|
2 |
|
2σ |
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2σ |
∆t q i=0 |
|
|
|
|
|
|
|
q i=0 l=1 |
|
|
|||||||||||
Это значит, что для моделирования передачи с отношением сигнал/шум E / N0 =γ нужно
назначить
σ 2 = 21γ 1 ∑∑q−1 Ns (si(l ) )2 q i=0 l=1
и использовать гауссовские псевдослучайные величины n(l ) с дисперсией σ 2 для моделирования выхода канала по формуле (П.2.4).
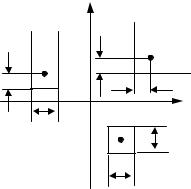
Приложение 3
Точное выражение для вероятности ошибки для КАМ
Вэтом разделе выводится точное выражение для вероятности ошибки при передаче
сиспользованием КАМ по каналу с АБГШ со спектральной плотностью мощности N0 / 2 .
Рассматривается случай, когда число сигналов q = 2m , где m - четное, то есть q = 4,16,64,256... и т.д. В этом случае сигнальное созвездие представляет собой полную
решетку (см. рис.16.1) и имеются три типа конфигурации решающих областей как показано на рис. П3.1. На рис. П3.1 символом ∆ обозначено минимальное евклидово расстояние между сигналами (сигнальными точками). Заметим, что существуют конфигурации решающих областей, полученных путем поворота конфигурации типов 1 и 2 на 90, 180 и 270 градусов. Они, очевидно, эквивалентны в канале с АБГШ конфигурациям типа 1 и типа 2 соответственно и поэтому отдельно не рассматриваются.
Тип 1 |
∆/ 2 |
Тип 2 |
|
|
|
∆/ 2 |
|
∆/ 2 |
|
|
|
|
∆ |
∆ Тип 3 |
∆
Рис. П3.1 Типы решающих областей
Точка в сигнальном пространстве, соответствующая принятому сигналу,
записывается как r = s +n , где |
s |
– |
сигнальная точка соответствующая переданному |
двумерному сигналу, n = (n1 , n2 ) |
– |
гауссовский случайный вектор, определяемый |
|
шумом. Случайные величины n1 |
и n2 |
(компоненты вектора n ) независимые и одинаково |
|
распределенные гауссовские случайные величины с нулевым математическим ожиданием и дисперсией N0 / 2 .
Рассмотрим вероятности ошибки при условии, что переданный сигнал имеет решающую область, относящуюся к одному из показанных на рис. П3.1 типов. Для трех указанных типов имеем следующие выражения для условных вероятностей ошибки; они получены как вероятности выхода точки, соответствующей принятому сигналу из решающей области, соответствующей переданному сигналу,
Pe (тип1) =1−Pr[−∆/ 2 < n1 < ∆/ 2]Pr[−∆/ 2 |
< n2 ] , |
|
Pe (тип2) =1−Pr[−∆/ 2 < n1 ]Pr[−∆/ 2 < n2 ] , |
|
(П3.1) |
Pe (тип3) =1−Pr[−∆/ 2 < n1 < −∆/ 2]Pr[−∆/ 2 < n2 |
< −∆/ 2] . |
|
Очевидно, что

|
|
∞ |
1 |
− |
x2 |
|
|
|
∞ |
1 |
|
|
− |
|
x2 |
|
|
|
∆ |
|
|
|
|
N0 |
|
|
|
|
|
|
N0 |
|
|
|
|||||||
Pr[−∆/ 2 < n1 ] = Pr[−∆/ 2 < n2 ] = ∫ |
e |
dx |
=1− |
∫ |
|
e |
|
dx =1 |
|
|
|
|||||||||
πN0 |
|
πN0 |
|
|
|
−Q |
2N0 |
|||||||||||||
|
−∆/ 2 |
|
|
|
|
|
∆/ 2 |
|
|
|
|
|
|
|
||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
∆/ 2 |
1 |
− |
x2 |
|
|
|
|
|
|
∆ |
|
|
Pr[−∆/ 2 < n1 < −∆/ 2] = Pr[−∆/ 2 < n2 < −∆/ 2] = |
∫ |
e |
N0 |
dx |
|
|
|
|
, |
|||||||||||
πN0 |
|
=1−2Q |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
−∆/ 2 |
|
|
|
|
|
|
|
|
2N0 |
|
||
где Q(x) = ∫x∞ (2π)−1/ 2 exp(−u2 / 2)du . Обозначим для удобства записи |
|
p = Q(∆/ |
||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||
учетом того, что ∆ = 6E /(q −1) (см. равенство (16.2)) , получаем, что |
|
|
|
|
||||||||||||||||
|
|
|
|
|
3E |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
p = Q |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
N |
0 |
q −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя (П3.2) и (П3.3) в (П3.1) получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
P (тип1) =1−(1−2 p)(1− p) = 3 p −2 p2 , |
|
|
|
|
|||||||||||||||
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P (тип2) =1−(1− p)2 = 2 p − p2 , |
|
|
|
|
|
|
|
|
|
||||||||||
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P (тип3) =1 − (1 − 2 p)2 |
= 4 p − 4 p2 , |
|
|
|
|
|
|
||||||||||||
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где вероятность p определена равенством (П3.4).
, (П3.2)
(П3.3)
 2N0 ). С
2N0 ). С
(П3.4)
(П3.5)
Найдем теперь вероятности передачи сигналов, относящиеся к различным типам. Полагая равновероятную передачу всех сигналов, нетрудно видеть, что
P(тип1) = 4( q −2) / q , |
|
P(тип2) = 4 / q , |
(П3.6) |
P(тип3) =1− P(тип1) − P(тип2) =1−4 / |
q + 4 / q . |
Безусловная вероятность ошибки вычисляется как |
|
Pe = Pe (тип1)P(тип1) + Pe (тип2)P(тип2) + Pe (тип3)P(тип3) ,
и окончательно, подставляя в это выражение правые части (П3.5), (П3.6) и (П3.4), после несложных преобразований получаем.
Pe = 4( |
|
|
|
|
|
q −( |
|
|
|
|
|
q −1) Q |
3E |
1 |
|
q −1)Q |
3E 1 |
|
. |
(П3.7) |
|||
|
q |
|
N0 |
q −1 |
|
|
|
N0 q −1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
На рис.П3.2 и П3.3 показаны графики зависимости вероятности ошибки и ее верхних границ в зависимости от отношения сигнал/шум для q =16 и q = 64 . Видно, что точность
верхних границ возрастает с увеличением числа сигналов q . Особенно точной оказывается граница, вычисленная по формуле (16.5).
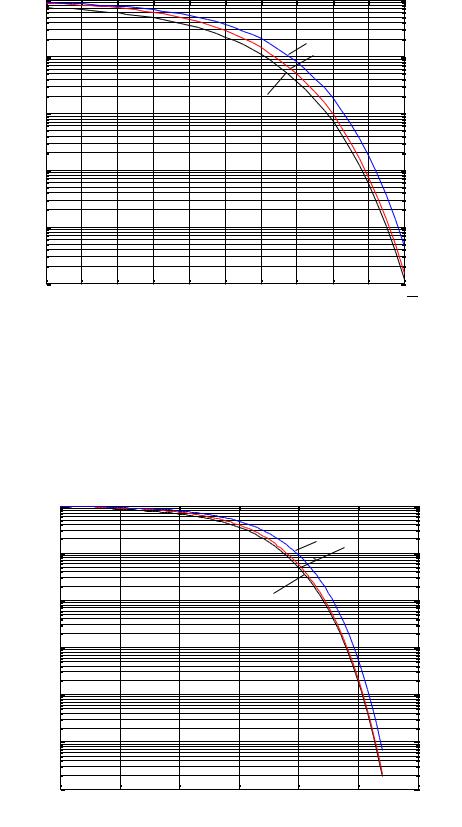
Pe |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
-1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
10-2 |
|
|
|
|
|
|
|
|
|
|
|
|
10-3 |
|
|
|
|
|
|
|
|
|
|
|
|
10-4 |
|
|
|
|
|
|
|
|
|
|
|
|
10-5 |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
E / N0 , дБ |
Рис.П3.2 Графики вероятности ошибки и двух верхних границ ошибки для КАМ-16, (1 –точное значение, 2 – верхняя граница (16.5) и 3 – верхняя граница (16.6)).
100 |
|
|
|
|
|
|
|
|
Pe |
|
|
|
|
|
|
|
|
10-1 |
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
||
10-2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
10-3 |
|
|
|
|
|
|
|
|
10-4 |
|
|
|
|
|
|
|
|
10-5 |
|
|
|
|
|
|
|
|
10-6 |
0 |
5 |
10 |
15 |
20 |
|
25 |
30 |
|
|
|
|
|
|
|
|
E / N0 , дБ |
Рис.П3.3 Графики вероятности ошибки и двух верхних границ ошибки для КАМ-64, (1 –точное значение, 2 – верхняя граница (16.5) и 3 – верхняя граница (16.6)).
