26.Относительная фазовая модуляция

Вканале со случайной фазой нельзя использовать сигналы ФМ. Эти сигналы различаются между собой начальной фазой, а случайный фазовый сдвиг, вносимый каналом, делает их неразличимыми на выходе канала даже в отсутствие шума. В частности, в двоичной системе передачи нельзя использовать двоичные противоположные сигналы, которые обеспечивают наилучшее соотношение между отношением сигнал/шум и вероятностью ошибки в канале с АБГШ.

Двоичные сигналы ЧМ в канале с АБГШ обеспечивают вероятность ошибки

что незначительно уступает (26.1). Однако в канале с АБГШ и неслучайной фазой можно применить ФМ (противоположные сигналы) и вероятность

ошибки при этом станет равной Pe ! Q( 2E / N0 ) , что соответствует выигрышу

в 3дБ в отношении сигнал/шум по сравнению с сигналами ЧМ (см. (26.1)).

Применение ФМ в канале со случайной фазой не только не дает выигрыша, но и вообще делает передачу невозможной. Однако при некоторых условиях в канале с АБГШ и случайной фазой можно получить зависимость вероятности ошибки от отношения сигнал/шум, определяемую равенством

что соответствует такому же выигрышу в 3дБ по сравнению с сигналами ЧМ.

Такую вероятность ошибки обеспечивает применение относительной фазовой модуляции (ОФМ) (DPSK, differential phase shift keying).

Сигналы двоичной ОФМ строятся следующим образом: при передаче символа “0” фаза текущего сигнала совпадает с фазой предыдущего сигнала, а

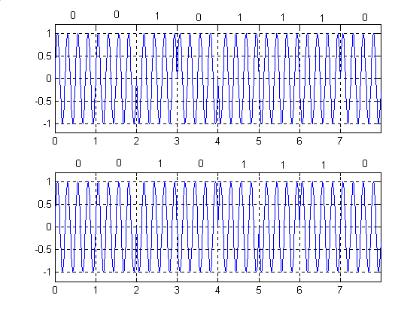
при передаче “1” фаза текущего сигнала меняется на противоположную по сравнению с предыдущим. Рис.26.1 дает представление о различии между сигналами двоичной ФМ и двоичной ОФМ.

Рис.26.1. Примеры сигнальных последовательностей ФМ (вверху) и ОФМ (внизу)

Из построения сигналов ОФМ следует, что информация передается разностью фаз двух смежных во времени сигналов в отличие от сигналов ФМ, в которых информация заключена в значении фазы текущего сигнала. Сигналы ОФМ могут применяться в канале со случайной фазой, если случайный фазовый сдвиг, определяемый каналом, меняется медленно по сравнению с

длительностью сигнала. Это значит, что сдвиг на двух соседних временных позициях остается примерно постоянным, и следовательно, разность фаз двух соседних по времени сигналов остается неизменной.

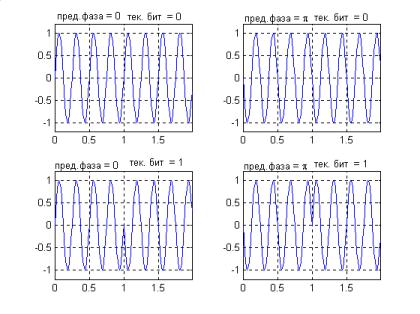
Рассмотрим сигналы ОФМ на двух соседних временных позициях. Легко заметить, что они представляют собой две пары сигналов с ортогональными огибающими, состоящими из двух чипов (см. рис.26.2), соответствующих знакам амплитуды (+,+) (+,-) или (-,-) (-,+) в зависимости от значения фазы предыдущего сигнала и текущего передаваемого бита.

Рис.26.2. Пары смежных ОФМ сигналов.

Нетрудно заметить, что пара возможных сигналов ОФМ,

соответствующих одному значению фазы предыдущего сигнала, может рассматриваться как пара сигналов с ортогональными огибающими длительности 2T ; очевидно, что энергия сигнала двойной длительности равна

2E , где E - энергия одиночного сигнала. Отсюда следует, что прием сигналов

ОФМ может быть реализован как прием двоичных сигналов с ортогональными огибающими на интервале 2T , то есть после небольшой модификации может быть использована схема, показанная на рис. 24.4. Для вероятности ошибки при использовании двоичных сигналов с ортогональными огибающими справедливо равенство (26.2), где E - энергия сигнала. Поскольку в случае ОФМ решение принимается на основе анализа сигнала двойной длительности,

то есть на основе анализа сигнала, имеющего двойную энергию, то для двоичных ОФМ сигналов формула для вероятности ошибки получается путем замены в (26.2) E на 2E , что дает в итоге выражение (26.3). Подчеркнем в заключение, что применение ОФМ возможно только при медленно изменяющейся фазе приходящих сигналов. Заметим также, что это условие не является очень сильным ограничением и часто выполняется на практике.