
- •Примеры базисов
- •Интегрирование
- •Определение
- •Аддитивная граница
- •25. Вероятность ошибки при оптимальном приеме в канале со случайной фазой
- •26. Относительная фазовая модуляция
- •27. Распределения Релея и Райса
- •28. Канал с замираниями. Модель с рассеивателями
- •32. Каналы с межсимвольной интерференцией. Оптимальный прием
- •Литература
8. Стационарные гауссовские случайные процессы
Введем необходимые обозначения. Пусть z ! (z1 , z2 ..., zL ) L -мерный |
случайный |
||
вектор. Обозначим многомерную |
функцию распределения |
вектора z как Fz (# , где |
|
! ( 1 , 2 ..., L ) . Она определена |
как Fz ( ) ! Pr[z1 1 , z2 |
2 ,..., zL L ]. |
Обозначим |
многомерную плотность вероятностей вектора z как wz ( ) , она равна
wz ( ) ! |
% L Fz ( ) |
|
. |
%1%2 ...% L |
|||
Введем обозначение для набора моментов времени t ! (t1 ,.t2 ,..., tk ) , k & 0 . Обозначим |
|||
вектор отсчетов одномерного случайного процесса |
|
x(t) , взятых в моменты времени |
|
t1 , t2 ,..., tk , как x(t) ! (x(t1 ), x(t2 ),..., x(tk )) . Случайный |
процесс называется стационарным, |
||
если wx(t ) ( ) ! wx(t( ) ( ) для всякого вектора с одинаковыми компонентами, ! ( , ,... ) ;
это значит, что функция плотности вероятности набора отсчетов не зависит от сдвига по оси времени.
Определение. Стационарный случайный процесс называется гауссовским, или
нормальным, если для любого k |
и любого набора моментов времени t ! (t1 , t2 ,..., tk ) |
|
||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
. |
1 |
|
|
1 |
|
T |
+ |
|
||||
|
wx(t ) ( ) ! |
|
|
|
|
|
|
|
|
exp, / |
|
( / m)0/ |
( / m) |
|
) . |
(8.1) |
||||||
(21 )k |
/ 2 (det 0)1/ 2 |
2 |
|
|||||||||||||||||||
|
|
|
|
|
− |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
□ |
Поясним выражение (8.1). В нем использовано |
обозначение m для вектора |
|||||||||||||||||||||
математических ожиданий, m ! 2 |
|
|
|
|
|
..., |
|
#. |
Заметим, что в силу стационарности |
|||||||||||||
x(t1 ), |
x(t2 ), |
x(tk ) |
||||||||||||||||||||
процесса x(t) |
|
! |
|
! ... ! |
|
! m . Далее, |
0 -- корреляционная матрица |
k 3 k , |
||||||||||||||
x(t1 ) |
x(t2 ) |
x(tk ) |
||||||||||||||||||||
определенная как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
79:11 |
:12 ... |
:1k 46 |
|
|
|
|
||||||||||
|
|
|
|
|
|
0 ! 7:21 |
:22 ... |
:2k 4 . |
|
|
|
|
||||||||||
|
|
|
|
|
|
7 ... ... ... |
... 4 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
7 |
|
:k 2 ... |
4 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
8:k1 |
|
:kk 5 |
|
|
|
|
||||||||
Элементы корреляционной матрицы задаются как

|
:il |
! (x(ti ) / |
x(ti ) |
)(x(tl ) / |
x(tl |
) |
) ! |
(x(ti ) / m)(x(tl ) / m) |
. |
|
|
(8.2) |
|||
|
:ii |
! |
|
! ; i2 , где |
|
; i2 - дисперсия i -го |
|
|
|
||||||
Заметим, что |
(x(ti ) / m)2 |
|
отсчета. |
В |
силу |
||||||||||
стационарности процесса x(t) |
дисперсии всех отсчетов равны между собой, т.е. ; i2 |
! ; 2 для |
|||||||||||||
всех i . И наконец, |
det 0 - |
обозначение определителя матрицы 0 . Из |
равенства |
(8.1) |
|||||||||||
следует, что многомерное гауссовское распределение полностью определяется корреляционной матрицей 0 и вектором математических ожиданий m .
Величины |
:il / ; i; l ! :il / ; 2 |
|
называются коэффициентами корреляции |
случайных |
|||||||||||||||||
величин x(ti ) и |
x(tl ) . Коэффициенты |
корреляции |
принимают |
значения |
из |
множества |
|||||||||||||||
[/1,(1] . Величины, имеющие нулевой коэффициент корреляции, |
|
|
|
называются |
|||||||||||||||||
некоррелированными. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выражение, стоящее в показателе экспоненты |
в выражении |
(8.1), |
может быть |
||||||||||||||||||
записано в компонентной форме, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
9 |
: |
: |
|
! |
: |
|
/1 |
|
1 |
/ m |
6 |
|
|
|
|
|
|
|
|
|
|
11 |
12 |
|
|
1k 6 |
|
9 |
|
||||
( / m)0/1 ( / m)T ! < |
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
4 |
|
7 |
|
|
4 |
|
|
/ m |
|
/ m |
! |
|
|
/ m= 7:21 |
:22 |
|
! :2k 4 |
|
7 2 |
/ m4 ! |
||||||||
|
|
1 |
|
2 |
|
|
k |
|
7 |
! ! ! !4 |
|
7 |
! |
4 |
|||||||
|
|
|
|
|
|
|
|
|
|
7 |
|
:k 2 |
|
|
|
4 |
|
7 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
8:k1 |
|
! :kk 5 |
|
8 k |
/ m5 |
||||||
k k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! >>(i / m):(il/1) (l / m) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i!1 l!1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где :(il/1) элементы матрицы 0/1 (обратной к 0 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 1. |
Пусть величины x(t1 ), x(t2 ),..., x(tk ) имеют нулевые математические |
||||||||||||||||||||
ожидания и не коррелированны, то есть, m ! (0,0,...,0) |
и |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
9; 2 |
0 |
" |
0 |
6 |
|
|
|
|
|
|
|
||||
|
0 ! diag(; 2 , |
|
|
7 |
|
0 |
; |
2 |
" |
0 |
4 |
|
|
|
|
|
|
|
|||
|
; 2 ,...,; 2 ) ! 7 |
|
|
4 . |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
7 |
" " " " |
4 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
7 |
|
|
0 |
" ; 2 |
4 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
7 0 |
4 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
8 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
Поскольку det 0 ! (; 2 )k и 0/1 ! diag(1/ ; 2 ,1/ ; 2 ,...,1/ ; 2 ) , то нетрудно видеть, что
|
. |
1 |
+ |
k |
. |
|
1 |
k |
|
+ |
k |
1 |
. |
|
2 |
+ |
k |
|
|
|
|
|
|||||||||||||
wx(t ) ( ) ! , |
1; ) |
|
exp, |
/ |
2; 2 |
> i |
) |
! ? |
1; exp, |
/ |
2; 2 |
) |
! ?wx(ti ) ( i ) . |
||||
|
− |
2 |
|
|
− |
|
|
i!1 |
|
|
i!1 |
2 |
− |
|
|
|
i!1 |
Последнее |
равенство |
означает, |
что |
компоненты |
вектора x(t) ! 2x(t1 ), x(t2 ),..., x(tk )# |
||||||||||||
независимы. |
Это |
значит, |
что |
|
некоррелированные |
гауссовские |
|
случайные величины |
|||||||||
независимы. Обратное верно для любого распределения, то есть независимые случайные величины не коррелированны. Иначе говоря, некоррелированность и независимость для гауссовских случайных величин эквивалентны. □
Пример 2. |
Пусть k ! 2 , m ! (m1 , m2 ) |
и 0 ! ; 2 |
9 |
1 |
6 |
; величина |
называется |
|
7 |
|
1 |
4 |
|||||
|
|
|
8 |
5 |
|
|
||
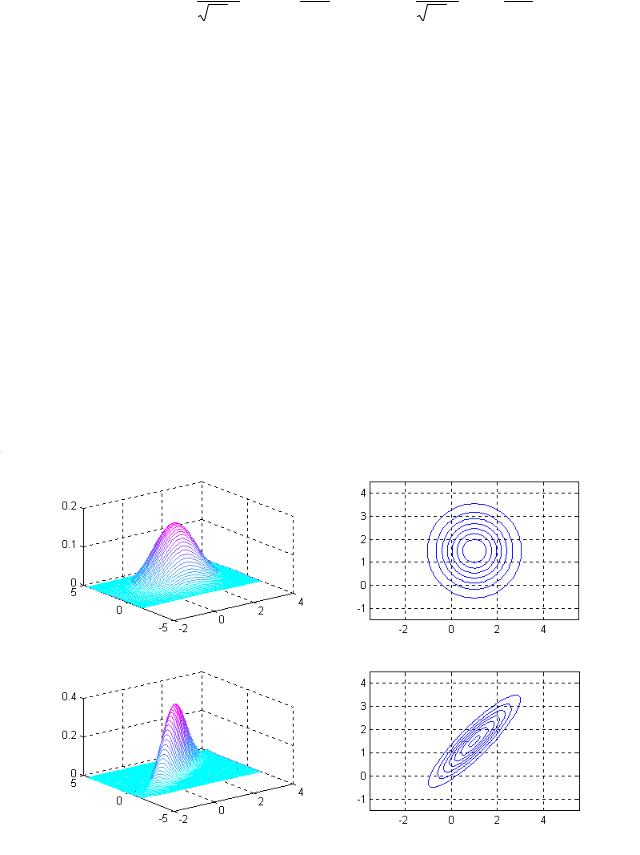
коэффициентом корреляции и лежит в интервале [/1,(1] . На рис.8.1 показаны графики функций плотности вероятностей wx ( ) вектора x ! (x1 , x2 ) для различных значений параметров распределения. Видно, что при ! 0 функция плотности вероятностей имеет
круговую симметрию относительно вертикальной оси, проходящей через точку (m1 , m2 ) . В
общем случае (при Α 0 ) линии уровня функции плотности вероятностей имеют вид
эллипсов.□
m1 ! 1 m2 ! 1.5
; 2 ! 1! 0
m1 ! 1 m2 ! 1.5
; 2 ! 1
! 0.9
а |
б |
Рис.8.1 Двумерная гауссовская плотность вероятностей; а) графики плотности, б) линии уровня
|
Вернемся к рассмотрению непрерывного времени. |
Далее будем считать, что |
||||||||||
процесс |
x(t) имеет нулевое математическое ожидание, |
то есть |
|
|
! 0 . Корреляционная |
|||||||
|
x(t) |
|||||||||||
функция |
стационарного |
процесса x(t) |
определяется |
как |
K x (t, ) ! |
|
. В |
силу |
||||
x(t)x(t ( ) |
||||||||||||
стационарности |
она не |
зависит от t , |
и поэтому можно |
писать K x ( ). Заметим, |
что |
|||||||
K x ( ) ! K x (/ ) |
и K x (0) |
! ; 2 . С учетом равенства (8.2) легко заметить, что :il ! K x (ti / tl ) . |
||||||||||
Это значит, что корреляционная функция определяет корреляционную матрицу для любого набора отсчетов, следовательно, корреляционная функция полностью задает описание стационарного гауссовского процесса с нулевым средним.
Преобразование Фурье корреляционной функции процесса |
x(t) |
называется |
|||||
спектральной плотностью мощности процесса x(t) , |
|
|
|
|
|
||
|
|
Sx ( f ) ! ΧΒKx ( )e/ j 21f d , |
|
|
|
|
|
|
|
/Χ |
|
|
|
|
|
и наоборот |
|
|
|
|
|
|
|
|
|
Kx ( ) ! ΧΒSx ( f )e j 21f df . |
|
|
|
|
|
|
|
/Χ |
|
|
|
|
|
Функция Sx ( f ) принимает действительные и неотрицательные значения. |
|||||||
Спектральная плотность мощности называется так потому, что интеграл вида |
F |
Sx ( f )df |
|||||
|
|
|
|
|
|
Β/F |
|
определяет |
среднюю мощность |
процесса x(t) в частотном |
интервале |
[/F, F ] . |
Полная |
||
мощность |
процесса может быть |
вычислена как P ! |
Χ S x ( f )df . Из одного |
из |
свойств |
||
|
|
|
Β/Χ |
|
|
|
|
преобразования Фурье (“площадь под кривой”) следует, что P ! |
Χ Sx ( f )df |
! K x (0) ! ; 2 , то |
|||||
|
|
|
|
Β/Χ |
|
|
|
есть средняя мощность процесса с нулевым математическим ожиданием численно равна его дисперсии. Поскольку спектральная плотность мощности однозначно связана с корреляционной функцией процесса, то она также как и корреляционная функция полностью определяет стационарный гауссовский процесс с нулевым средним.
На рис.8.2 показаны три примера корреляционной функции, спектральной плотности мощности и типичной реализации гауссовского случайного процесса. Первый пример соответствует слабо коррелированному (быстро изменяющемуся) процессу, его спектр мощности почти равномерен. Во втором примере корреляция больше, а спектр – уже. Третий пример соответствует процессу с наибольшей корреляцией и наименее узким спектром.
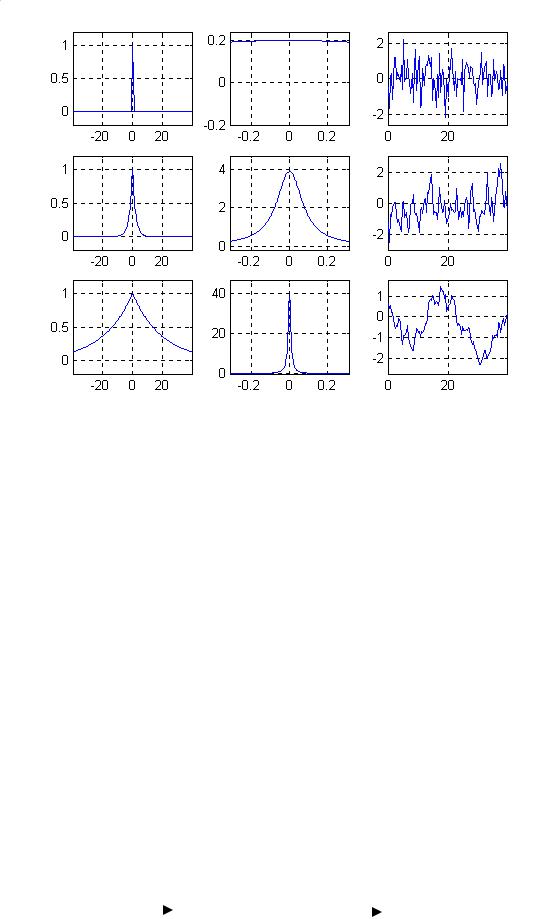
а |
б |
в |
Рис.8.2. Примеры гауссовских случайных процессов, а) корреляционная функция, б) спектральная плотность мощности, в) типичная реализация
Линейное преобразование (в частности, фильтрация) гауссовского случайного процесса не изменяет распределение (т.е. процесс остается гауссовским), но меняет его спектральную плотность мощности. Линейный фильтр задается импульсной переходной характеристикой h(t) или связанной с ней преобразованием Фурье частотной характеристикой H ( f ) , H ( f ) h(t) . Реализация случайного процесса на выходе фильтра равна свертке реализации на входе с импульсной переходной характеристикой фильтра.
Спектральная плотность процесса на выходе равна S y ( f ) !| H ( f ) |2 S x ( f ) . Таким образом,
линейное преобразование меняет в общем случае спектр и корреляционную функцию процесса; см. рис. 8.2.
x(t) |
Линейный |
y(t) ! h(t) Ε x(t) |
|
|
||
|
|
фильтр |
|
|
|
|
|
|
h(t) H ( f ) |
|
|
|
|
Sx ( f ) |
S y ( f ) !| H ( f ) | |
2 |
S x ( f ) |
|||
|
|
|||||
Рис.8.2. Линейная фильтрация случайного процесса

9. Белый гауссовский шум
Формально белый гауссовский шум (БГШ) определяется как гауссовский
случайный процесс n(t) с нулевым |
средним |
( |
n(t) |
= 0 ) |
и постоянной |
|||||||
спектральной плотностью мощности Sn ( f ) = N0 / 2 . Пусть g(t) |
произвольная |
|||||||||||
функция с конечной нормой, то есть |
|
|
|
g |
|
|
|
< ∞ . |
Тогда случайная величина, |
|||
|
|
|
|
|||||||||
определенная как
ng = ∞∫g(t)n(t)dt ,
−∞
обладает следующими свойствами: а) ng – гауссовская случайная величина
(г.с.в.), б) ng = 0 , в) ng2 = (N0 / 2)
 g
g 
 2 . Случайная величина ng может рассматриваться как скалярное произведение n(t) и g(t) , то есть ng = (g, n) .
2 . Случайная величина ng может рассматриваться как скалярное произведение n(t) и g(t) , то есть ng = (g, n) .
Найдем корреляционную функцию БГШ. Известно, что K n (τ) ↔ Sn ( f )
Поскольку Sn ( f ) = N0 / 2 , то Kn (τ) = (N0 / 2)δ(τ) .
В дальнейшем будет использоваться одно важное свойство БГШ, сформулированное в виде следующего утверждения.
Утверждение. Скалярные произведения БГШ и ортогональных функций независимы.
Доказательство. Пусть ϕ1 (t) иϕ2 (t) - ортогональные функции, т.е. (ϕ1 ,ϕ2 ) = 0 . Скалярные произведения БГШ и функций ϕ1 (t) и ϕ2 (t) определены как
n1 = (n,ϕ1 ) = ∞∫n(t)ϕ1 (t)dt , n2 = (n,ϕ2 ) = ∞∫n(t)ϕ2 (t)dt .
−∞ |
−∞ |
Требуется доказать, что n1 и n2 |
независимы. По определению БГШ n1 и n2 это |
г.с.в. Найдем корреляционный момент (корреляцию) этих величин n1n2 . Эта величина равна
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∞∫n(t)ϕ1 (t)dt |
∞∫n(t' )ϕ2 (t' )dt' = ∞∫ ∞∫ϕ1 (t)ϕ2 (t' ) |
|
dtdt' . |
|||||||||
|
|
|
n1n2 |
n(t)n(t' ) |
||||||||||||||
|
|
|
|
|
|
|
−∞ |
−∞ |
−∞−∞ |
|
|
|
|
|
||||
Поскольку |
|
|
= K n (t −t' ) = (N0 / 2)δ(t −t' ) , то |
|
|
|
|
|||||||||||
n(t)n(t' ) |
|
|
|
|
||||||||||||||
|
|
|
|
N0 |
|
∞ ∞ |
|
|
N0 |
∞ |
∞ |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
n1n2 |
= |
|
∫ ∫ϕ1 (t)ϕ2 (t' )δ(t −t' )dtdt' = |
∫ϕ1 |
|
∫ϕ2 |
|
|
|
|||||||||
2 |
|
2 |
(t) |
(t' )δ(t −t' )dt' dt = |
||||||||||||||
|
|
|
|
|
−∞−∞ |
|
|
−∞ |
|
−∞ |
|
|
|
|||||
|
N |
0 |
∞ |
|
= |
|
ϕ1 (t)ϕ2 (t)dt = 0 . |
||
2 |
||||
|
−∫∞ |
|||
Переход в третьем равенстве основан на использовании фильтрующего свойства δ -функции, а последний переход – на ортогональности функций ϕ1 (t)

и ϕ2 (t) . Таким образом доказано, что а) n1 и n2 - гауссовские случайные величины, б) n1 и n2 не коррелированны. Отсюда следует, что n1 и n2
независимы. □ Дисперсия случайного процесса, как уже отмечалось, может быть
вычислена как σ 2 = ∫−∞∞ Sn ( f )df . Для БГШ Sn ( f ) = N0 / 2 для − ∞ < f < ∞ .
Таким образом, для БГШσ 2 = ∞. Это значит, что БГШ реально не может существовать, так как имеет бесконечно большую мощность. В то же время БГШ часто используется в качестве математической модели для описания помех, действующих в реальных системах и расчета характеристик таких систем. Приведем объяснение этого кажущегося противоречия (см. рис.9.1).
Шум, действующий в реальных условиях, имеет спектр мощности гладкий в некоторой полосе и спадающий к нулю за ее пределами. Полоса любого реального устройства имеет ширину, меньшую, чем ширина полосы реального шума. Поэтому, реакция реального устройства на реальный шум и реакция реального устройства на идеализированный шум (БГШ) совпадают. Иными словами, поскольку БГШ никогда не рассматривается сам по себе, а рассматривается только результат его фильтрации (реакция устройства на шум), то проблем, связанных с бесконечно большой дисперсией на входе устройства, просто не возникает. На выходе реального устройства появляется в точности такой же процесс, как если бы на входе был БГШ.
|
|
Частотная характеристика |
|
|
реальной системы |
|
|
Спектр мощности |
|
|
идеализированного шума |
|
|
(БГШ) |
0 |
|
|
0 |
f |
Спектр мощности |
|
реального шума |
Рис.9.1. Спектры мощности реального и идеализированного шума.

10. Оптимальный прием дискретных сигналов
Задача оптимального приема дискретных сигналов формулируется
следующим образом. Имеется q сигналов s0 (t) ,…, sq!1 (t) . При передаче
случайно выбирается один из них в соответствии с вероятностным
распределением P0 ,…, Pq!1 , Pi 0 , iq#!01 Pi # 1. Приемник наблюдает выход |
|
канала |
r(t) . Задача приемника состоит в определении номера переданного |
сигнала |
i! , i! # 0,..., q ! 1. При этом возможно, что решение приемника будет |
ошибочным. |
Оптимально построенный |
приемник обеспечивает наименьшую |
||||||||||||
вероятность ошибки Pe |
# Pr[i! % i] (см. рис. 10.1) |
|
|
|
||||||||||
Сообщение |
i |
|
si (t) |
|
r(t) |
|
Решение i! |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Модулятор |
|
|
|
Канал |
|
|
|
Демодулятор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
(передатчик) |
|
|
|
|
|
|
(приемник) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.10.1 Cистема передачи дискретных сигналов
Пусть для представления сигналов выбран базис {& j (t)} , j # 1,2,..., D .
Тогда сигнальному множеству {si (t)} с использованием этого базиса ставится в
соответствие множество сигнальных точек {si }, si R D . Если разложить по базису сигнал на выходе канала r(t) , то получим точку (вектор) r . Канал формально может быть задан набором условных плотностей вероятностей w(r | si ) , i # 0,1,2,..., q ! 1. Процесс передачи можно тогда описать как показано
на рис. 10.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Передатчик: |
|
|
|
Канал: |
|
|
Приемник: |
|
|
Выбор s {si } |
в |
|
|
w(r | s0 ) |
r |
|
Определение |
! |
|
s |
|
|
номера |
i |
||||
|
соответствии |
с |
|
|
w(r | s1 ) |
|
|
переданного |
|
|
распределением |
|
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
|
|
|
.... |
|
|
сигнала |
|
|
|
{Pi } |
|
|
|
|
|
|
||
|
|
|
|
w(r | s q!1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.10.2 Формальная модель передачи дискретных сигналов
Для описания приема (процесса формирования решения о переданном сигнале) используем понятие решающей области. Разобьем некоторым образом множество всех возможных значений вектора r на q непересекающихся
областей R , i # 0,1,..., q !1, , т.е. " R # R D , R # R |
j |
# ( . Решение о переданном |
||||
i |
i |
i |
i |
|
|
|
|
|
|
|
|
|
|
сигнале принимается по правилу i! # i , если |
r R . Понятно, что вероятность |
|||||
|
|
|
|
|
|
i |
ошибки зависит от конфигурации |
решающих |
областей Ri . Поэтому задача |
||||
построения оптимального приемника может быть переформулирована как задача построения решающих областей, обеспечивающих минимальную вероятность ошибки.
Пусть Pe (r) |
вероятность ошибки при условии, что принятый вектор |
|
равен r . Тогда безусловная вероятность ошибки равна |
||
|
|
q!1 |
|
Pe # )Pe (r)w(r)dr # )Pe (r)w(r)dr . |
|
|
RD |
i#0 Ri |
Для всякого r Ri |
имеем |
Pe (r) # 1! Pr[i | r] , где Pr[i | r] – вероятность |
принятия решения в пользу i -го сигнала при условии, что полученный вектор равен r . Тогда вероятность ошибки равна
q!1 |
|
Pe # 1! )Pr[i | r]w(r)dr . |
(10.1) |
i#0 Ri
Чтобы вероятность ошибки была минимальной, должна быть максимальной сумма в правой части (10.1), то есть нужно назначить решающие области таким образом, чтобы эта сумма была максимальной. Поскольку решающие области не пересекаются, то условие максимизации суммы эквивалентно максимизации каждого слагаемого этой суммы, то есть значения интеграла )Ri Pr[i | r]w(r)dr .
Так как подынтегральное выражение неотрицательно, то легко видеть, что значение этого интеграла максимально, если положить
Ri # r : Pr[i | r]w(r) Pr[i, | r]w(r),−i, % i+
или, исключая из определения области несущественный для этого множитель,
получим |
|
Ri # r : Pr[i | r] Pr[i, | r], −i, % i+. |
(10.2) |
Вероятности Pr[i | r] это апостериорные вероятности приема i . Поэтому прием решений с использованием решающих областей (10.2) называется приемом по максимуму апостериорной вероятности (МАВ). С использованием формулы Байеса имеем Pr[i | r] # w(r | i)Pi / w(r) , тогда равенство (10.2) можно переписать в виде
R( МАВ) # r : w(r | i)P w(r | i,)P |
,−i, % i+. |
(10.3) |
||
i |
i |
i, |
|
|
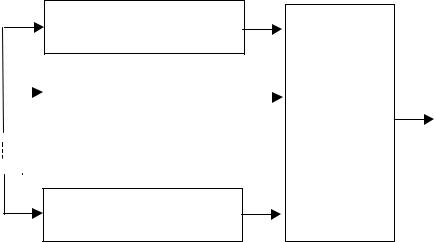
Тогда алгоритм оптимального приема можно записать следующим образом: по принятому из канала сигналу вычислить вектор r коэффициентов разложения по базису и положить i! # k , если r Rk , где решающие области определены равенством (10.3). Иллюстрация приведена на рис. 10.3.
Вычисление значения w(r | 0)P0
|
|
|
|
Вычисление значения |
|
Выбор |
! |
r |
w(r | 1)P1 |
|
i |
||||
|
максимума |
||||||
|
|
||||||
|
|
|
|
|
|
|
|
Вычисление значения w(r | q !1)Pq!1
Рис.10.3 Схема оптимального приемника (приемника по МАВ)
На практике часто встречается случай, когда сигналы передаются равновероятно, то есть Pi # 1/ q для всех i , i # 0,1,..., q !1. В этом случае
определение решающих областей и оптимального приемника можно упростить,
исключив из определения (10.3) одинаковые априорные вероятности.
Получающийся в этом случае алгоритм носит название приема по максимуму правдоподобия (МП), а решающие области принимают вид
|
|
|
R( МП) # r : w(r | i) w(r | i,),−i, % i+. |
(10.4) |
|||
|
|
|
i |
|
|||
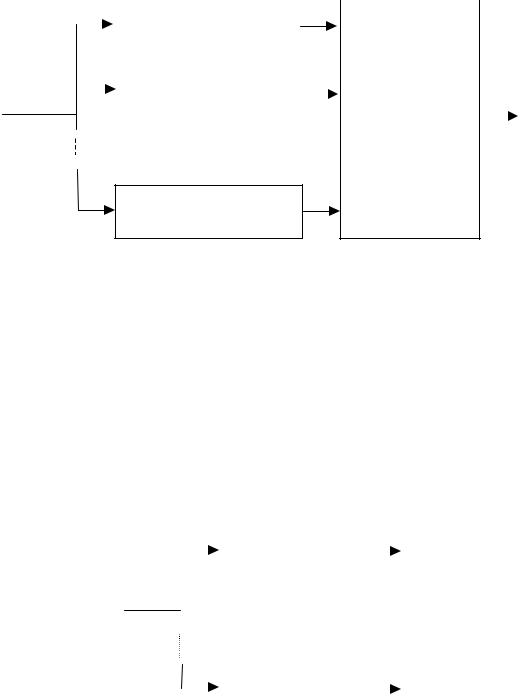
Схема приемника, принимающего решения по МП, показана на рис 10.4. |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Вычисление значения |
|
|
|
|
|
|
|
w(r | 0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычисление значения |
|
Выбор |
! |
||
|
|
|
|
|
i |
|||
r |
w(r | 1) |
|||||||
|
максимума |
|||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Вычисление значения w(r | q !1)
Рис.10.4 Схема оптимального приемника (приемника по МП)
Заметим, что приемник МП является оптимальным только в случае равновероятных сигналов.
На практике приемник может быть построен следующим образом. Сначала по принятому сигналу вычисляется вектор r (см. рис. 10.5) , а затем производится обработка этого вектора как это показано на рис. 10.3 и 10.4.
|
|
|
Вычисление |
|
r1 |
1 |
|
||
|
|
|
|
T r(t)& (t)dt |
|
|
|||
|
|
|
r # |
|
|
. |
|
||
|
|
|
|
|
|
||||
|
|
|
1 |
)0 |
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
||
r(t) |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
. |
# r |
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
rD |
. |
|
|
|
|
Вычисление |
|
|
||||
|
|
|
|
. |
|
||||
|
|
|
|
T |
|
|
|
/ |
|
|
|
|
|
|
|
|
|
||
|
|
|
rD # )0 |
r(t)& D (t)dt |
|
|
|
|
|
Рис.10.5. Вычисление компонент вектора r
