
- •Примеры базисов
- •Интегрирование
- •Определение
- •Аддитивная граница
- •25. Вероятность ошибки при оптимальном приеме в канале со случайной фазой
- •26. Относительная фазовая модуляция
- •27. Распределения Релея и Райса
- •28. Канал с замираниями. Модель с рассеивателями
- •32. Каналы с межсимвольной интерференцией. Оптимальный прием
- •Литература
Методы передачи дискретных сообщений
Конспект лекций
(апрель 2010)
© 2001-2010 А.Н.Трофимов
Кафедра информационных систем
С-Петербургский Государственный Университет Аэрокосмического Приборостроения
2001-2004-2007-2010
Введение
В этом документе представлен конспект лекций по курсу “Методы передачи дискретных сообщений”, читавшийся студентам кафедры информационных систем факультета систем управления Санкт-Петербургского государственного университета аэрокосмического приборостроения в 1995-2004гг. В конспекте представлены практически все вопросы, входящие в лекционную часть курса. Первая редакция этого конспекта относится к 2001 г.

1. Структура системы передачи информации. Модели каналов и помех.
Самая общая структура системы передачи информации показана на рис.1.1.
|
|
m |
! |
|
|||
|
|
m |
|||||
Источник |
|
|
|
Канал |
|
|
|
сообщений |
|
|
|
|
|
Получатель |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Рис.1.1 Общая схема системы передачи информации
Здесь под каналом понимается часть системы передачи, природа и характеристики которой заданы, а их изменение нежелательно, затруднено или просто невозможно. Задача,
решаемая системой передачи, состоит в том, чтобы передать сообщение m от источника к
получателю. Как правило, сообщение источника представлено в такой форме, в которой
невозможна его эффективная передача по каналу. Поэтому в систему обычно включаются устройства передачи и приема, которые выполняют преобразование сообщения m в сигнал
s и преобразование принятого сигнала r |
в принятое сообщение |
! |
(см. рис.1.2). |
||||||||||||
m |
|||||||||||||||
|
|
m |
|
s |
|
r |
|
! |
|
||||||
|
|
|
|
|
|
m |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Источник |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сообщений |
|
|
Передатчик |
|
|
Канал |
|
|
Приемник |
|
|
|
Получатель |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.1.2 Схема системы передачи информации |
|
|||
Заметим, |
что преобразование m → |
s , выполняемое передатчиком, является взаимно |
|||
однозначным и |
детерминированным; |
преобразование s → r , |
определяемое |
каналом, |
|
является случайным; преобразование |
r → |
! |
передатчике, |
является |
|
m , выполняемое в |
|||||
детерминированным, но не взаимно однозначным.
Если источник порождает сообщения из конечного множества, то он называется источником дискретных сообщений, в противном случае источник называется источником непрерывных сообщений.
Процесс формирования сигнала по сообщению называется модуляцией. В процессе модуляции выполняется изменение параметров сигнала в соответствии с сообщением,
подлежащим передаче. Если множество сигналов, формируемых в процессе модуляции,
оказывается конечным, то такая модуляция называется дискретной или цифровой. В
настоящем курсе рассматривается передача с использованием дискретной модуляции. Более подробная схема передачи дискретных сообщений с использованием цифровой модуляции показана на рис. 1.3.
m
|
Источник |
|
|
|
Кодер |
|
|
|
|
Кодер |
|
|
|
|
|
|
|
|
s(t) |
|
дискретных |
|
|
|
источника |
|
|
|
|
канала |
|
|
|
Модулятор |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
сообщений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Канал |
|
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получатель |
|
|
|
Декодер |
|
|
|
|
Декодер |
|
|
|
|
|
|
|
|
r(t) |
|
|
|
|
источника |
|
|
|
|
канала |
|
|
|
Демодулятор |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кодек |
|
|
|
|
Кодек |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
источника |
|
|
|
|
канала |
|
|
|
Модем |
|
|
|||
Рис. 1.3 Схема системы передачи дискретных сообщений

Кодирование-декодирование источника служит для уменьшения избыточности,
присутствующей в сообщениях источника. В результате кодирования сообщения источника оказываются записанными с использованием меньшего числа символов, то есть эти сообщения представляются в сжатой форме. Кодирование источника может выполняться с потерями (например, сжатие звука и изображений, представленных в цифровой форме), либо без потерь (например, архивирование файлов).
Канальное, или помехоустойчивое, кодирование-декодирование применяется для обеспечения большей надежности передачи. При использовании помехоустойчивого кодирования скорость передачи уменьшается за счет передачи избыточных символов,
позволяющих исправлять ошибки, возникающие в канале. Вообще говоря, в системе передачи информации операции кодирования-декодирования источника и/или помехоустойчивого кодирования-декодирования могут отсутствовать.
На рис.1.4 показана структура системы цифровой передачи непрерывных сообщений.
|
|
|
|
|
|
Исходный цифровой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
m(t) |
(двоичный) поток |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналого- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Источник |
|
|
|
|
|
Кодер |
|
|
|
|
Кодер |
|
|
|
|
|
|
|
|
|
s(t) |
||||
|
|
|
|
|
цифровое |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
непрерывных |
|
|
|
|
преобразо- |
|
|
|
|
источника |
|
|
|
|
канала |
|
|
|
Модулятор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
сообщений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вание |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Канал |
||
! |
|
|
|
Принятый |
|
цифровой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
(двоичный) поток |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
m(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Цифро- |
|
|
|
|
Декодер |
|
|
|
|
Декодер |
|
|
|
|
|
|
|
|
|
r(t) |
|
Получатель |
|
|
|
|
аналоговое |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
источника |
|
|
|
|
канала |
|
|
|
Демодулятор |
|
|
|
|
||||
|
|
|
|
|
преобразо- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вание |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кодек |
|
|
|
|
Кодек |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
источника |
|
|
|
|
канала |
|
|
|
Модем |
|
|
|
|||
Рис. 1.4 Схема цифровой системы передачи непрерывных сообщений

Непрерывное сообщение источника подвергается дискретизации и квантованию
(аналого-цифровому преобразованию); в результате этой операции формируется цифровой поток. Дальнейшая передача выполняется так же как показано на рис.1.3. После приема цифрового потока непрерывное сообщение источника восстанавливается с использованием цифро-аналогового преобразования и интерполяции (сглаживания).
Качество системы передачи дискретных сообщений характеризуется вероятностью ошибки, которая определяется как
Pe = |
! |
Pr[m ≠ m] , |
где m - переданное сообщение, ! - полученное сообщение. Само сообщение может иметь m
различный объем: от одного бита до нескольких тысяч бит в зависимости от назначения системы передачи сообщений. При передаче непрерывных сообщений в качестве критерия
качества рассматривается некоторая мера близости сообщения ! , доставленного m(t)
получателю, и оригинального сообщения m(t) . Наиболее часто используется среднеквадратичное отклонение
|
2 |
|
1 |
T |
! |
2 |
|
∆ |
|
= lim |
|
∫(m(t) − |
m(t)) |
|
dt |
|
T |
|
|||||
|
|
T → ∞ |
0 |
|
|
|
или отношение ∆ 2 / P , где
P = lim 1 T∫ m(t)2 dt
T → ∞ T 0
мощность непрерывного сообщения. Следует отметить, что малое значение среднеквадратичного отклонения не всегда соответствует хорошему воспроизведению непрерывного сообщения, например, звукового. В этом случае используется другая мера
отклонения, например, такая max |
|
m(t) − |
! |
|
. |
|
|
||||
|
m(t) |
|
|||
0< t < T |
|
|
|
|
|
Основными параметрами системы передачи являются скорость передачи, ширина полосы частот и отношение сигнал/шум. Эти параметры обычно являются исходными, и
при заданных значениях этих параметров требуется обеспечить требуемое качество передачи.
Помехи, действующие в канале передачи информации, можно разделить на помехи
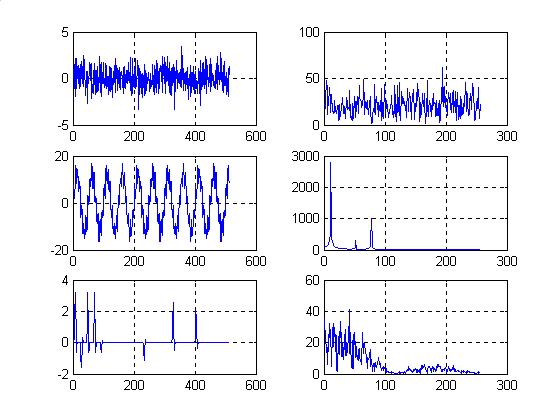
естественного происхождения и помехи искусственного происхождения, которые в свою очередь делятся на преднамеренные и непреднамеренные. По своему действию на передаваемый сигнал помехи могут быть аддитивными и мультипликативными. Среди аддитивных помех различаются а) тепловой шум, б) сосредоточенная помеха, в) импульсная помеха, г) помехи от других систем передачи. На рис.1.5 показаны типичные реализации некоторых аддитивных помех (слева) и их спектральное представление (справа).
а |
б |
Рис.1.5 Аддитивные помехи: шум, сосредоточенная, импульсная (сверху вниз); а) типичные реализации, б) типичные спектры
Видно, что спектр сосредоточенной помехи сконцентрирован в нескольких узких участках частотного диапазона, а сама сосредоточенная помеха занимает всю временную область. Импульсная помеха представляет собой последовательность коротких по сравнению с длительностью полезного сигнала импульсов, то есть импульсная помеха сосредоточена во временной области. Спектр импульсной помехи достаточно протяжен в частотной области. Реализация теплового шума занимает всю временную область. Спектр теплового шума занимает всю частотную область и имеет примерно равную интенсивность на всех частотах.
2. Геометрическое представление сигналов
|
|
|
|
Начнем с напоминания необходимых определений и обозначений. |
|
|
|
|
Пусть некоторые |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
функции g(t) и h(t) определены на интервале |
[a, b] . |
Величина ∫ab g(t)h(t)dt называется |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
скалярным |
произведением функций |
g(t) |
и h(t) |
|
|
|
и обозначается |
|
|
|
как |
|
|
|
|
(g, h) . Величина |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
b |
g |
2 |
(t)dt |
|
1/ 2 |
|
|
|
|
|
|
функции |
g(t) |
|
и обозначается как |
|
|
|
|
|
g |
|
|
|
|
. |
|
|
|
Заметим, что |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
∫a |
|
|
|
|
называется нормой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(g, g) = |
|
g |
|
|
|
2 |
. |
Наконец, |
величина |
(g(t) − h(t)) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
расстоянием, |
точнее |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
∫a |
|
dt |
называется |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
говоря, евклидовым расстоянием, |
между функциями g(t) |
и |
h(t) и обозначается |
d (g, h) . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Очевидно, |
|
|
|
что |
d(g, h) = |
|
g − h |
|
. Кроме |
того очевидно, что |
|
g − h |
|
|
|
|
|
2 = |
|
g |
|
|
|
2 |
− 2(g, h) + |
|
|
|
h |
|
|
|
2 . |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Аналогично |
определяются расстояние, |
норма и |
|
|
скалярное |
произведение |
|
|
|
для векторов |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a = (a1 ,..., an ) |
|
и |
b = (b1 ,..., bn ) : |
|
|
|
|
d (a, b) = (∑nj=1 (a j −bj )2 )1/ 2 , |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
= (∑nj=1 a2j )1/ 2 , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(a, b) = ∑nj=1 a j bj |
. Легко видеть также, что |
|
|
|
a −b |
|
|
|
2 |
= |
|
|
|
a |
|
|
|
2 |
− 2(a, b) + |
|
|
|
b |
|
|
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
Пусть сигнал s(t) |
определен на конечном интервале времени, |
например на [0,T ] , где |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
T |
- |
период следования сигналов. Пусть {ϕ j (t)} , j =1,2,..., |
множество ортонормированных |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
функций, |
|
|
определенных |
|
|
на интервале |
|
[0,T ] , то |
|
есть |
таких, для |
|
|
|
которых выполняется |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
условие |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, |
i = k, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ϕi ,ϕk ) = ∫ϕi (t)ϕk (t)dt = |
δik = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
≠ k. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Сигнал s(t) |
может быть представлен в виде линейной комбинации D базисных функций |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s(t) = ∑s jϕ j (t) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.1) |
||||||||||||||||||||||||||||||
j=1
Величина D называется размерностью пространства сигналов. Заметим, что D может быть конечной или бесконечной величиной. По поводу размерности D следует сделать пару замечаний.
Замечание 1. Пусть {si (t)}, i = 0,..., q −1, некоторое фиксированное сигнальное множество. Тогда существует алгоритм построения базиса {ϕ j (t)} , j =1,..., D , и D ≤ q ,
причем равенство имеет место только тогда, когда сигналы {si (t)} линейно независимы.
Алгоритм построения базиса по набору сигналов {si (t)} называется процедурой Грама– Шмидта (см. Приложение 0). □
Замечание 2. Если сигнальное множество не фиксировано, но все сигналы имеют конечную норму, то существует универсальный базис {ϕ j (t)} , с помощью которого можно представить любой сигнал. Число базисных функций в этом случае может быть бесконечным. □
Вернемся к рассмотрению равенства (2.1), называемого также обобщенным рядом Фурье. Величины s j в (2.1) называются коэффициентами разложения сигнала s(t) по базису
{ϕ j (t)} . Найдем как коэффициенты разложения связаны с сигналом. Для этого умножим
левую и правую части равенства (2.1) на ϕk (t) и проинтегрируем на интервале [0,T ] , т.е.
вычислим
T |
T |
D |
|
|
D |
T |
D |
|
|
|
|
|
= ∑s j ∫ϕ j (t)ϕk (t)dt = ∑s jδ jk = sk . |
||
∫s(t)ϕk (t)dt = ∫ |
∑s jϕ j (t) ϕk (t)dt |
||||||
0 |
0 |
j=1 |
|
|
j=1 |
0 |
j=1 |
Таким образом, k -ый коэффициент разложения вычисляется следующим образом |
|||||||
|
|
|
sk = T∫s(t)ϕk (t)dt = (s,ϕk ) . |
(2.2) |
|||
|
|
|
|
0 |
|
|
|
Собирая вместе равенства (2.1) и (2.2), получим в итоге пару преобразований |
|||||||
|
|
|
|
|
D |
|
|
|
|
|
s(t) = ∑s jϕ j (t) |
|
|||
|
|
|
|
|
j=1 |
|
(2.3) |
|
|
|
|
T |
|
|
|
|
|
|
s j = ∫s(t)ϕ j (t)dt |
|
|||
|
|
|
|
0 |
|
|
|
которые ставят во взаимное соответствие сигнал s(t) и набор коэффициентов s = (s1 , s2 ,..., sD ) что будем обозначать как
{ϕ j (t )}
s(t) ↔ s .
Далее рассмотрим случай сигнального множества конечной размерности, т.е. D < ∞.
В этом случае имеет место отображение сигнального множества {si (t)} в множество сигнальных векторов, или сигнальных точек в D -мерном вещественном пространстве RD
{ϕ j (t )} |
|
{si (t)} ↔ {si } RD |
(2.4) |
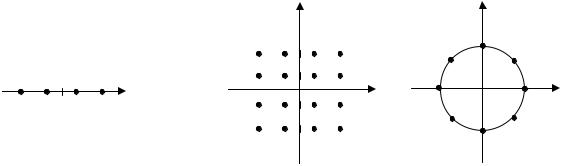
Для значений размерности D ≤ 3 множество сигнальных точек может быть изображено графически. Такое изображение называется иногда сигнальным созвездием (signal constellation). Примеры сигнальных созвездий показаны на рис. 2.1.
а) |
б) |
в) |
Рис.2.1 Примеры сигнальных созвездий а) D =1 , б,в) D = 2
Рассмотрим свойства отображения (2.4).
Свойство 1. Представление (2.3) дает наилучшее приближение при любом
фиксированном числе слагаемых. □ |
|
|
|
~ |
N |
N ≤ D . Покажем, что |
|
Пусть s (t) = ∑j=1 c jϕ j (t) , где c j -- некоторые коэффициенты, |
|||
если коэффициенты |
|
~ |
будут |
c j назначены равными коэффициентам s j из (2.2), то s (t) и s(t) |
|||
близки в некотором смысле. Обозначим через ∆ величину рассогласования между |
~ |
||
s (t) и |
|||
|
|
|
|
|
|
|
|
T |
|
~ |
s(t) и определим ее как квадрат расстояния между функциями, т.е. ∆ = ∫0 |
(s(t) − s (t)) |
|||||||||
Найдем значения коэффициентов c j , |
минимизирующие |
∆ , решая уравнение |
∂∆ / ∂c j |
|||||||
Подробнее, |
|
|
|
|
|
|
|
|
|
|
T |
~ |
|
2 |
T |
|
N |
|
2 |
|
|
|
|
|
|
|
|
|
||||
∆ = ∫(s(t) − s (t)) |
|
dt =∫ s(t) − |
∑ckϕk (t) dt , |
|
|
|||||
0 |
|
|
|
0 |
|
k =1 |
|
|
|
|
2dt .
=0 .
тогда
|
∂∆ |
|
T |
∂ |
|
N |
|
2 |
|
T |
|
N |
|
|
|
|
= |
∫0 |
|
s(t) − ∑ckϕk (t) |
dt = −2 |
|
s(t) − ∑ckϕk |
(t) ϕj (t)dt = |
|||||
|
∂c j |
∂c j |
|
|||||||||||
|
|
|
k =1 |
|
|
∫0 |
k =1 |
|
|
|||||
T |
|
|
|
|
N |
T |
|
|
|
|
N |
|
= −2(s j −c j ) = 0 . |
|
= −2∫s(t)ϕj (t)dt + 2∑ck |
∫ϕk (t)ϕj (t)dt = −2 s j − ∑ck δkj |
|||||||||||||
0 |
|
|
|
|
k =1 |
0 |
|
|
|
|
k =1 |
|
|
|
Отсюда следует, что при |
c j |
= s j |
рассогласование между |
~ |
и s(t) минимально. Заметим |
|||||||||
s (t) |
||||||||||||||
также, что при N = D это рассогласование равно нулю. □
Свойство 2. Энергия, или квадрат нормы сигнала равна квадрату нормы (квадрату длины) соответствующего сигнального вектора, т.е.
T |
T |
T |
D |
D |
T |
D |
||||||||
E = ∫s2 (t)dt =∫s(t)s(t)dt = ∫s(t)∑s jϕ j (t)dt =∑s j ∫s(t)ϕ j (t)dt =∑s j s j = |
|
|
|
s |
|
|
|
2 . |
||||||
|
|
|
|
|||||||||||
0 |
0 |
0 |
j=1 |
j=1 |
0 |
j=1 |
||||||||
□
Свойство 3. Скалярное произведение сигналов равно скалярному произведению соответствующих сигнальных векторов, т.е. (s1 , s2 ) = (s1 ,s2 ) ;
T |
T |
D |
D |
T |
D |
∫s1 (t)s2 (t)dt = ∫s1 (t)∑s2 jϕ j (t)dt = ∑s2 j ∫s1 (t)ϕ j (t)dt = ∑s2 j s1 j = (s1 ,s2 ) . |
|||||
0 |
0 |
j=1 |
j=1 |
0 |
j=1 |
□ |
|
|
|
|
|
Свойство |
4. Отображение |
(2.4) |
изометрично |
т.е. сохраняет расстояние, |
|
d(s1 , s2 ) = d(s1 ,s2 ) ; иными словами расстояние между сигнальными функциями совпадает с расстоянием между соответствующими сигнальными точками. □
Рассмотрим квадрат расстояния между сигналами
T T T T
d 2 (s1 , s2 ) = ∫(s1 (t) − s2 (t))2 dt =∫s12 (t)dt − 2∫s1 (t)s2 (t)dt + ∫s22 (t)dt =
0 |
|
|
|
|
0 |
0 |
0 |
||||||||||
= |
|
|
|
s1 |
|
|
|
2 − 2(s1 , s2 ) + |
|
|
|
s2 |
|
|
|
2 = d 2 (s1 , s2 ) . |
|
|
|
|
|
|
|
|
|
|
|||||||||
Замечание. Перечисленные свойства отображения (2.4) справедливы независимо от конкретного вида базиса, который может быть выбран многими способами.
Примеры базисов. Рассмотрим два примера универсальных, или функционально полных, базисов. Эти базисы содержат бесконечно много функций и могут использоваться для представления любых сигнальных функций.
1. Ортонормированный гармонический базис. Пусть 0 ≤ t ≤T .
|
ϕ0 |
(t) = |
1 |
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
t |
|
|
|
ϕ1 |
(t) = |
2 |
|
|
|
|
|
|||
|
T |
sin 2π |
T |
|
|
||||||
|
|
|
|
|
|
|
|
||||
|
ϕ2 |
(t) = |
2 |
|
|
2π |
t |
|
|||
|
T |
cos |
T |
|
|||||||
|
|
|
|
|
|
|
|||||
|
ϕ3 |
(t) = |
2 |
|
|
|
2t |
||||
|
T |
sin 2π |
T |
|
|||||||
|
|
|
|
|
|
|
|||||
|
ϕ4 |
(t) = |
2 |
|
|
2π |
2t |
||||
|
T |
cos |
T |
|
|||||||
|
L |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что множитель |
2 / T обеспечивает |
нормировку функций базиса. Графики |
|||||||||
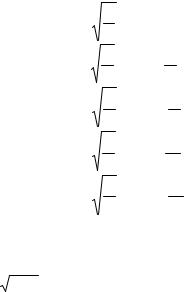
нескольких первых функций гармонического базиса показаны на рис.2.2. □ |
|||||||||||
2.Ортономированный базис Уолша (Walsh) Сначала определим функции wn (τ) на |
|||||||||||
интервале τ [−1/ 2,1/ 2] . Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
τ |
|
>1/ 2 |
|
|||
|
|
|
|
|
|
||||||
|
w0 (τ) = |
|
|
|
|
≤1/ 2 |
, |
||||
|
|
τ |
|
|
|||||||
|
|
|
|
||||||||
|
|
|
1, |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
а все остальные функции более высокого порядка определяются рекурсивно |
|||||||||||
w2n+ p (τ) = (−1)[n / 2]+p (wn (2τ +1/ 2) + (−1)n+p wn (2τ −1/ 2)). |
|||||||||||
Функции wn (τ) , n = 0,1,..., |
ортогональны и нормированы на интервале [−1/ 2,1/ 2] . Графики |
||||||||||
нескольких первых функций базиса Уолша показаны на рис.2.2. □
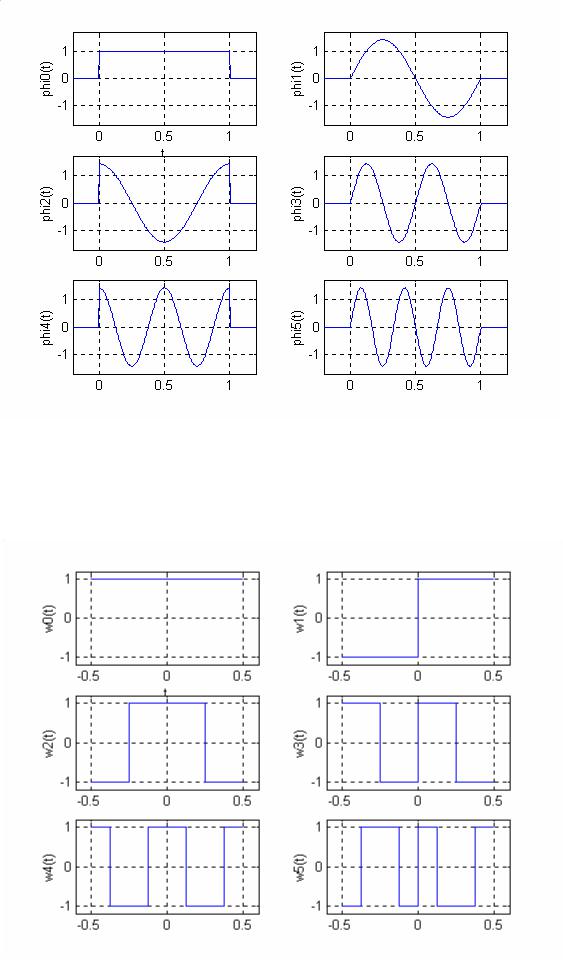
Рис.2.1 Функции гармонического базиса, заданные на интервале [0,1]
Рис.2.2 Функции Уолша.
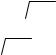
Если положить t = (τ +1/ 2)T , то t [0,T ] , если τ [−1/ 2,1/ 2] . Поэтому, множество
функций ϕn (t) , определенных какϕn (t) =  1/ T wn (t / T −1/ 2) , образуют ортонормированный
1/ T wn (t / T −1/ 2) , образуют ортонормированный
базис на интервале [0,T ] . Множитель  1/ T обеспечивает, как и ранее, нормировку функций базиса.
1/ T обеспечивает, как и ранее, нормировку функций базиса.
3. Периодические сигналы и ряд Фурье
Если для сигнала s(t) выполняется условие s(t) = s(t ± T ) , то он называется
периодическим. Наименьшее T , для которого это условие выполняется, называется периодом сигнала.
Рассмотрим интервал [− T / 2,T / 2] . В качестве базиса возьмем гармонический базис,
рассмотренный ранее |
|
|
|
|
|
|
|
|
|
|
|
1 |
, k = |
0, |
|
|
|
|
|
|
|
T |
|
|
|
|
|||
|
|
|
|
t(k + 1) / 2 |
|
||||
ϕ k (t) = |
|
2 |
|
k = 1,3,5,... |
|||||
|
T |
sin 2π |
T |
|
|
, |
|||
|
|
|
|
|
|
|
|
||
|
|
2 |
cos |
2π |
t(k / 2) |
, |
k = |
2,4,6,... |
|
|
|
T |
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
||
Заметим, что этот базис обладает свойством ортонормированности не только на интервале [0,T ] , но и на интервале [− T / 2,T / 2]. Вычислим коэффициенты разложения
|
|
T / 2 |
|
|
sk = (s,ϕ k ) = |
∫ s(t)ϕ k (t)dt |
(3.1) |
|
|
− T / 2 |
|
Тогда для t |
[− T / 2,T / 2] справедливо представление |
|
|
|
s(t) = ∑ |
skϕ k (t) |
(3.2) |
|
k |
|
|
Если распространить область определения базисных функций{ϕ k (t)} с |
интервала |
||
[− T / 2,T / 2] |
на всю ось времени, то они станут периодическими с периодом T . Поскольку |
||
сигнал s(t) |
имеет период T , то равенство (3.2) будет выполняться и для t (−∞ |
, ∞ ) . Это |
|
значит, что обобщенный ряд Фурье для периодических функций и для гармонического базиса совпадает с обычным рядом Фурье.
Обычно ряд Фурье записывается в форме |
|
|
|
|
s(t) = a0 / 2 + |
∑∞ (ak cos 2π fk t + |
bk sin 2π fk t) , |
(3.3) |
|
|
k = 1 |
|
|
|
где fk = k / T . Найдем значения коэффициентов ряда Фурье ak , |
bk из (3.3), исходя из |
|||
выражений (3.1) для коэффициентов |
обобщенного ряда |
Фурье |
(3.2). Ряд (3.2) можно |
|
переписать в виде |
|
|
|
|
s(t) = s0ϕ 0 (t) + s1ϕ 1 (t) + s2ϕ 2 (t) + s3ϕ |
3 (t) + |
s4ϕ 4 (t) + |
... = |
|
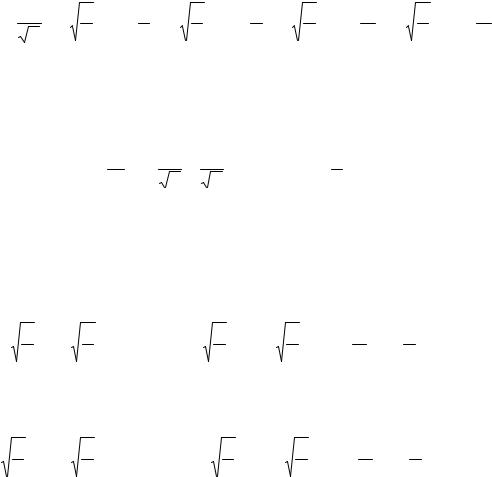
= s |
|
1 |
+ |
s |
2 |
sin 2π |
|
t + |
s |
|
2 |
cos 2π |
t + |
|
s |
|
2 |
sin 2π |
2t |
+ |
s |
|
2 |
cos 2π |
2t |
+ ... |
|||||
|
0 |
T |
1 T |
|
|
T |
|
2 T |
|
|
|
|
T |
|
|
3 T |
|
|
|
T |
|
|
4 T |
|
T |
|
|||||
Аналогично, ряд (3.3) можно переписать в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
s(t) = |
a0 / 2 + |
|
a1 cos 2π f1t + b1 sin 2π |
f1t + |
a2 cos 2π f2 t + |
b2 sin 2π f2t |
|
|
||||||||||||||||||||
Из сравнения двух последних выражений видно, что |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
a0 |
= |
s0 |
1 |
= |
1 |
T / 2 |
|
|
|
|
|
= |
1 |
T / 2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
2 |
T |
T |
|
∫ s(t)ϕ 0 (t)dt |
T |
|
∫ s(t)dt |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
− T / 2 |
|
|
|
|
|
|
− T / 2 |
|
|
|
|
|
|
|
||||||||
отсюда следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
T / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a0 = |
|
∫ s(t)dt , |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
T − |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ak = |
|
2 |
s2k |
= |
2 |
T / 2 |
|
|
(t)dt = |
2 |
T / 2 |
s(t) |
|
2 |
|
|
|
|
kt |
|
|
2 |
T |
/ 2 |
|
|
|||||
|
T |
T |
∫ s(t)ϕ 2k |
T |
|
∫ |
|
T |
cos 2π |
|
dt = |
T |
∫ s(t) cos 2π fk tdt |
||||||||||||||||||
|
|
|
|
− T / 2 |
|
|
|
|
|
− T / 2 |
|
|
|
|
|
|
|
T |
|
|
− T / 2 |
|
|
||||||||
и
bk = |
2 |
s2k − 1 |
= |
2 |
T / 2 |
2 |
T / 2 |
2 |
|
kt |
T |
T |
∫ s(t)ϕ 2k − 1 (t)dt = |
T |
∫ s(t) |
T |
sin 2π |
dt = |
|||
|
|
|
− T / 2 |
− T / 2 |
|
T |
2 |
T / 2 |
∫ s(t) sin 2π fk tdt . |
|
T |
− T / 2 |
Итак, периодический сигнал может быть представлен рядом (3.3), с коэффициентами
|
|
|
|
2 |
T / 2 |
|
|
|
|
|
||
|
|
a0 = |
∫ s(t)dt , |
|
||||||||
|
|
|
T |
|
||||||||
|
|
|
|
|
− T / 2 |
|
|
|
|
|
||
|
|
2 |
T / 2 |
|
|
|
|
|
k |
|
||
ak |
= |
|
∫ |
s(t) cos |
2π |
|
|
|
t dt , |
|||
T |
|
T |
||||||||||
|
|
− T / 2 |
|
|
|
|
|
|
||||
|
|
2 |
T / 2 |
|
|
|
|
k |
|
|||
bk |
= |
|
∫ |
s(t) sin |
2π |
|
|
|
t dt . |
|||
T |
T |
|||||||||||
|
|
− T / 2 |
|
|
|
|
|
|||||
4. Комплексная форма ряда Фурье
Ранее получено выражение для ряда Фурье
s(t) = a0 / 2 + ∑∞ |
(ak cos 2π |
fk t + bk sin 2π fk t) , |
||||||||||||||
где |
|
|
k = 1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
T / 2 |
|
|
|
|
|
|
||
|
|
|
a0 |
= |
∫ s(t)dt |
|
|
|
|
|
||||||
|
|
|
T |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
− T / 2 |
|
|
|
|
|
|
||
|
|
2 |
T |
/ 2 |
|
|
|
|
|
k |
|
|
||||
ak |
= |
|
|
|
∫ |
s(t) cos 2π |
|
|
|
|
t dt |
|||||
T |
|
T |
|
|||||||||||||
|
|
− T / 2 |
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
T |
/ 2 |
|
|
|
|
k |
|
|
||||
bk |
= |
|
|
|
∫ |
s(t) sin |
2π |
|
|
|
t dt . |
|||||
T |
T |
|||||||||||||||
|
|
− T / 2 |
|
|
|
|
|
|
||||||||
Его можно преобразовать с использованием формул Эйлера для тригонометрических
функций: cos x = (e jx + e− |
jx ) / 2 |
и sin x = (e jx − |
e− jx ) / 2 j , где |
j = |
|
− 1 , то есть |
|||||||||||||||||||||
|
|
a |
|
|
|
∞ |
|
|
|
e j 2π fkt + e− j 2π fkt |
|
|
|
e j 2π fkt − |
e− j2π fkt |
|
|||||||||||
s(t) = |
|
|
|
0 |
+ |
∑ |
|
a |
|
|
|
|
|
|
|
|
+ b |
|
|
|
|
|
|
|
= |
||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
k |
|
|
|
2 j |
|
|
|
|||||||
|
|
|
|
k= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
a0 |
∞ |
|
|
ak |
− |
jbk |
|
|
|
|
|
ak + jbk |
|
|
j2π fkt |
|
||||||||
|
|
|
+ ∑ |
|
|
|
j2π fkt |
|
|
|
− |
|
|||||||||||||||
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
+ |
|
|
|
|
e |
|
|
|
|
||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
||||||||||
|
|
|
|
|
k = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Обозначим коэффициент при exp( j2π |
fk t) как ck , а коэффициент при exp(− j2π fk t) как c− k . |
||||||||||||||||||||||||||
Очевидно, что ck = (ak − jbk ) / 2 и c− k обозначений имеем запись ряда Фурье
s(t)
= |
(a |
k |
+ jb |
) / 2 . Кроме того, |
c |
k |
= |
c* |
k |
. C учетом этих |
|
|
|
k |
|
|
|
|
− |
|
|||
в комплексной форме |
|
|
|
|
|
|
|||||
|
∑∞ |
|
|
k |
|
|
|
|
|
|
|
= |
|
ck e j 2π |
|
t , |
|
|
|
|
|
(4.1) |
|
|
T |
|
|
|
|
|
|||||
k = −∞
где
|
ak − jbk |
|
1 |
T / 2 |
|
k |
|
||
ck = |
= |
∫ s(t)e |
− j 2π |
|
t dt . |
(4.2) |
|||
T |
|||||||||
2 |
T |
|
|||||||
|
|
− T / 2 |
|
|
|
|
|||
Равенства (4.1) и (4.2) допускают любопытную графическую интерпретацию. (См. рис. 4.1 – он пока не нарисован)
5. Преобразование Фурье и спектры сигналов
Ряд Фурье дает разложение периодического сигнала по гармоническому ортонормированному базису. Сигнал общего вида (т.е. непериодический) можно представить как "предельный" случай периодического сигнала при T → ∞.
В общем случае вместо ряда Фурье рассматривается преобразование Фурье, определенное как
S( f ) = ∞∫s(t)e− j 2πft dt , |
(5.1) |
−∞ |
|
и обратное преобразование Фурье |
|
s(t) = ∞∫S( f )e j 2πft df |
(5.2) |
−∞ |
|
Формулы (5.1) и (5.2) имеют определенное сходство с формулами ряда Фурье в комплексной форме и коэффициентами этого ряда соответственно
|
|
|
|
|
|
1 |
|
T / 2 |
|
|
|
|
|
|
k |
|
|
|
|
|
|||
|
ck |
= |
|
∫ |
s(t)e |
− j |
2π |
|
|
t dt , |
|
(5.3) |
|||||||||||
|
|
T |
|
||||||||||||||||||||
|
T |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
−T / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
k |
|
|
|
|
|
||
|
|
|
|
s(t) = ∑ck e j |
2π |
|
t . |
|
(5.4) |
||||||||||||||
|
|
|
|
T |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
k =−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Действительно, если подставить правую часть равенства (5.3) в (5.4), то получим, что |
|||||||||||||||||||||||
|
∞ 1 |
|
T / 2 |
|
|
− j 2π |
k |
t |
|
|
|
j 2π |
k |
t |
|
|
|||||||
|
|
|
|
|
∫ s(t)e |
|
|
T |
|
|
|
|
T |
. |
|
||||||||
s(t) = ∑ |
|
|
|
|
|
|
dt e |
|
|
|
|
||||||||||||
|
k =−∞ T |
|
−T / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Предельный переход при T → ∞ соответствует заменам: а) |
1/T на df , б) k /T на f , и |
||||||||||||||||||||||
в) ∑∞k =−∞K на ∫−∞∞Kdf . Выполняя этот предельный переход, получаем, что |
|||||||||||||||||||||||
∞ |
∞ |
− j 2πft |
|
|
|
j 2πft |
|
|
|
∞ |
|
|
|
j 2πft |
|
||||||||
|
∫s(t)e |
dt |
|
df |
= ∫S( f )e |
df , |
|||||||||||||||||
s(t) = ∫ |
|
|
|
|
e |
|
|
|
|||||||||||||||
−∞ |
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
||||
1442443 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
=S ( f ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
то есть получаем равенства (5.1) и (5.2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Функция S( f ) , определенная равенством (5.1), называется спектральной плотностью или спектром сигнала s(t) . Также функция S( f ) называется преобразованием или образом функции s(t) , которая иногда называется оригиналом. Преобразование Фурье является взаимно-однозначным преобразованием; символически это преобразование будет
обозначаться как s(t) ↔ S( f ) . В настоящем курсе рассматриваются вещественные сигналы.
Спектр даже в этом случае представляет собой комлекснозначную (принимающую комплексные значения) функцию вещественной переменной. Поэтому можно записать, что
S( f ) = S( f ) e jθ ( f ) = S( f ) cosθ( f ) + j S( f ) sinθ( f ) ,
где S( f ) - амплитудный спектр (модуль комплексного спектра), θ( f ) - фазовый спектр.
Квадрат амплитудного спектра S( f ) 2 называется энергетическим спектром. Кроме того, имеют место соотношения
S( f ) = (Re S( f ))2 + (Im S( f ))2 ,
θ( f ) = arctan Im S( f ) . Re S( f )
Рассмотрим подробнее вопрос о соотношении вещественной и мнимой составляющей
спектра. Для этого рассмотрим произвольный вещественный сигнал s(t) . Он может быть
представлен в |
виде |
суммы четной |
sч (t) |
и нечетной |
sн (t) функций, |
то есть |
|
s(t) = sч (t) + sн (t) , |
где |
sч (t) = (s(t) + s(−t)) / 2 |
и |
sн (t) = (s(t) − s(−t)) / 2 . |
Найдем |
||
преобразование Фурье от s(t) |
|
|
|
|
|
||
S( f ) = ∞∫s(t)e− j 2πft dt = ∞∫(sч (t) + sн (t))e− j 2πft dt = ∞∫(sч (t) + sн (t))(cos 2πft − j sin 2πft)dt = |
|||||||
−∞ |
|
−∞ |
|
−∞ |
|
|
|
∞∫sч (t) cos 2πftdt − j ∞∫sн (t) sin 2πftdt + ∞∫sн (t) cos 2πftdt − j ∞∫sч (t) sin 2πftdt . |
|
||||||
−∞ |
|
−∞ |
−∞ |
|
|
−∞ |
|
|
|
|
1442443 |
1442443 |
|
||
|
|
|
|
=0 |
|
=0 |
|
Два последних слагаемых равны нулю, потому что они получены в результате
интегрирования нечетной функции (произведения sн (t) |
на четную функцию cos(...) или |
произведения sч (t) на нечетную функцию sin(...) ) |
в симметричных пределах |
интегрирования. Таким образом, |
|
S( f ) = ∞∫sч (t) cos 2πft dt − j |
∞∫sн (t) sin 2πft dt , |
−∞ |
−∞ |
откуда следует, что
Re S( f ) = ∞∫sч (t) cos 2πift dt ,
−∞
Im S( f ) = − ∞∫sн (t) sin 2πift dt .
−∞
Два последних равенства означают, что четная функция имеет вещественный спектр, а
нечетная - мнимый, |
или sч (t) ↔ Re S( f ) , sн (t) ↔ Im S( f ) . Повторим, что в общем случае |
||||||||||||||||
спектр комплексный. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим важные примеры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
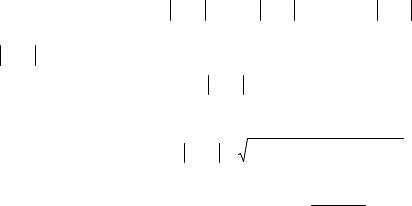
Пример 1. Пусть сигнал задан равенством |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
−t / T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s(t) = |
( A / T )e |
|
|
, t ≥ 0 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
t < 0 |
|
|
|
|
|
|
|
|
|
где A > 0 , T > 0 . График сигнала показан на рис.5.1. Вычислим его спектр |
|
|
|||||||||||||||
S( f ) = ∞∫s(t)e− j 2πft dt = |
A |
∞∫e−t (1/T + j 2πf ) dt |
= − |
|
A / T |
|
e−t (1/T + j 2πf ) |
|
∞ |
= |
|
|
A |
. |
|||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||
T |
1/ T + j2πf |
|
|
1 |
+ j2πfT |
||||||||||||
−∞ |
|
0 |
|
|
|
|
|
0 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Амплитудный и фазовый спектры равны соответственно |
|
|
|
|
|
|
|
|
|
||||||||
|
S( f ) = |
A |
, |
θ( f ) = arctan(−2πfT ) . |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 + (2πfT )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Графики амплитудного и фазового спектров показаны на рис. 5.1. □ s(t)
S( f ) |
S( f ) |
θ( f ) |
θ( f ) |
а б
Рис.5.1 Сигнал из примера 1, его амплитудный и фазовый спектры;
а) A =1, T = 4 , б) A =1, T =1 .
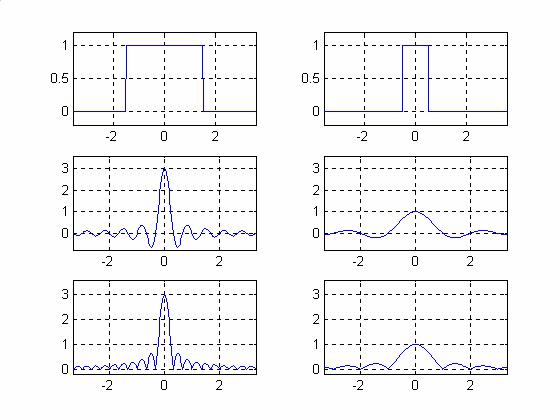
Пример 2. Спектр прямоугольного импульса. Пусть сигнал задан равенством
|
|
A, |
|
| t |≤T / 2 |
|
|
|
|
|
|
|||||
|
|
s(t) = |
|
|
t |
|
>T / 2 |
, |
|
|
|
|
|
||
|
|
0, |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где A > 0 , T > 0 . График сигнала показан на рис.5.2. Вычислим его спектр |
|||||||||||||||
S( f ) = ∞∫s(t)e− j 2πft dt = A T∫/ 2 |
e− j 2πft dt = − |
A |
e− j 2πft |
|
T / 2 |
= |
|||||||||
|
|||||||||||||||
|
|
||||||||||||||
j2πf |
|||||||||||||||
|
−∞ |
−T / 2 |
|
|
|
|
|
|
|
|
|
−T / 2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
A |
(e jπfT − e− jπfT )= |
|
A |
sin πfT |
= AT sin πfT . |
|
||||||||
j2πf |
|
|
|||||||||||||
|
|
πf |
|
|
πfT |
|
|||||||||
Графики спектра и амплитудного спектра показаны на рис. 5.2.
s(t) |
s(t) |
S( f ) |
S( f ) |
| S( f ) | |
| S( f ) | |
а |
б |
Рис.5.2 Сигнал из примера 2, его спектр и амплитудный спектр;
а) T = 3, A =1 , б)T =1, A =1
Как видно из выражений для спектра и из графиков, показанных на рис.5.2, спектр прямоугольного импульса имеет бесконечную ширину. Это значит, что на практике в
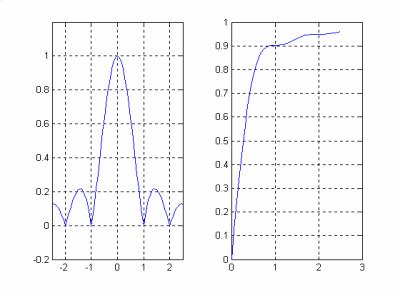
точности прямоугольный импульс не может существовать. То, что в инженерной практике называется прямоугольным импульсом, представляет собой лишь некоторое приближение к нему с передним и задним фронтами конечной, а не бесконечной, крутизны. На практике за ширину спектра прямоугольного сигнала принимается величина равная W =1/ T , где T длительность сигнала. Это так называемая ширина главного лепестка графика спектра. Такое соглашение обосновывается тем, что в интервале частот от −W до W содержится более 90% энергии прямоугольного импульса. На рис.5.3 приведены амплитудный спектр и график величины
|
fmax |
|
E( fmax ) = |
∫| S( f ) |2 |
df , |
|
− fmax |
|
представляющей собой часть энергии |
сигнала в |
полосе [− fmax , fmax ] . Видно, что |
E(1/ T ) > 0.9E(∞). |
E( fmax ) |
|
| S( f ) | |
|
f / T |
fmax / T |
Рис.5.3 Амплитудный спектр прямоугольного импульса и его энергия в зависимости от полосы частот
Пример 3. Спектр δ -функции. |
|
Напомним основное свойство δ -функции, которое можно рассматривать как ее |
|
определение. Пусть g(t) некоторая функция, тогда |
|
∞∫g(t)δ(t −t0 )dt = g(t0 ) . |
(5.5) |
−∞ |
|
Равенство (5.5) известно также как фильтрующее свойство δ -функции. Функция δ(t)
может также рассматриваться как "предел" |
функции δτ (t) , определенной как |
|||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
δτ (t) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
τ , | t |<τ / 2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
0, | t |≥τ / 2 |
|
||||
Поясним смысл этого утверждения. Для этого рассмотрим предел |
||||||||||||||
|
|
|
|
|
∞ |
|
|
|
|
|
|
1 |
t0 +τ / 2 |
|
|
|
|
|
lim |
∫ |
g(t)δτ (t −t0 )dt =lim |
∫ |
g(t)dt . |
||||||
|
|
|
|
τ |
||||||||||
|
|
|
|
τ→0 |
|
|
|
|
|
τ→0 |
|
|||
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
t0 −τ / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
Пусть G(t) - первообразная функции g(t) , т.е. G (t) = g(t) . Тогда |
||||||||||||||
|
1 |
t |
+τ |
/ 2 |
|
|
1 |
|
|
|
|
|
|
|
lim |
0 |
∫ |
g(t)dt = lim |
(G(t0 +τ / 2) −G(t0 |
−τ / 2))= G′(t0 ) = g(t0 ) . |
|||||||||
τ |
|
|
||||||||||||
τ→0 |
t0 |
τ→0 |
τ |
|
|
|
|
|
|
|||||
|
|
−τ |
/ 2 |
|
|
|
|
|
|
|
|
|
|
|
Таким образом
∞ |
|
|
lim |
g(t)δτ (t −t0 )dt =g(t0 ) . |
(5.6) |
τ→0 −∞∫ |
|
|
Сравнивая равенства (5.5) и (5.6), можно заметить, что δ -функция может рассматриваться как предельный случай короткого и мощного прямоугольного импульса. Заметим, что это не единственный способ такого "предельного" описания δ -функции.
Вернемся к рассмотрению спектра δ -функции. Преобразование Фурье δ -функции имеет вид
∞∫δ(t)e− j 2πft dt = e− j 2πft |
|
t =0 =1. |
|
||
−∞ |
|
|
Последнее равенство означает, что спектральная плотность δ -функции постоянна на всей частотной оси. □
6. Свойства преобразования Фурье
Прямое и обратное преобразования Фурье определяются как
S( f ) = |
∞∫ s(t)e− j 2π ft dt , |
|
− ∞ |
s(t) = |
∞∫ S( f )e j2π ft df , |
−∞
исимволически обозначаются как s(t) ↔ S( f ) . Рассмотрим важнейшие свойства преобразования Фурье.
Линейность. Если g(t) ↔ |
G( f ) , h(t) ↔ |
H ( f ) , то ag(t) + bh(t) ↔ aG( f ) + bH ( f ) , где |
|
a и b постоянные. |
|
|
|
Доказательство очевидно.□ |
|
|
|
Площадь под кривой. Пусть g(t) ↔ G( f ) . Тогда |
|||
∞∫ g(t)dt = G(0) , |
∞∫ G( f )df = g(0) . |
||
− |
∞ |
|
− ∞ |
Доказательство. |
|
|
|
|
G( f ) = |
∞∫ g(t)e− j 2π ft dt |
|
|
|
− ∞ |
|
Положив в левой и правой части этого равенства f = 0 , получим искомое утверждение. Второе равенство доказывается аналогично с заменой прямого преобразования на обратное. (Полезно проверить это свойство для примеров, рассмотренных ранее.) □
Сдвиг по времени и по частоте. Пусть g(t) ↔ |
G( f ) , тогда g(t − t0 ) ↔ e− j 2π ft0 G( f ) , |
||||||
G( f − f0 ) ↔ |
e j 2π f0t g(t) . |
|
|
|
|
||
Доказательство. Найдем преобразование Фурье от g(t − t0 ) |
|||||||
∞∫ g(t − t0 )e− j 2π ft dt = |
|
Замена переменной : |
|
|
∞∫ g(t1 )e− j 2π f (t0 + t1 ) dt1 = |
||
|
|
|
|||||
|
t1 = t − t0 , dt1 = dt, t = t1 + t0 |
= |
|||||
− |
∞ |
|
|
|
|
|
− ∞ |
|
|
|
|
|
|
||
|
= e− j 2π ft0 |
∞∫ g(t1 )e− j 2π ft1 dt1 = e− j 2π ft0 G( f ) . |
|||||
|
|
|
|
− ∞ |
|
|
|
Свойство сдвига по частоте доказывается аналогично. Из этого свойства следует, что при сдвиге по времени амплитудный спектр не меняется, т.к.
