Мартынов_силаI

R2 – активное сопротивление вторичной обмотки, приведенное к виткам вторичной обмотки трансформатора;

Rв.д – динамическое сопротивление тиристора.

С учетом угла коммутации γ падение напряжения на активных сопротивлениях схемы URγ:

– для трехфазной мостовой и кольцевой схем выпрямления

∆URγ = 3π IdRôæççè23π -2γö÷÷÷ø;

– для двойной трехфазной схемы выпрямления с уравнитель-

При α = 0° угол коммутации γ = γ0:

γ0 =arccosæçççç1- xôId ö÷÷÷÷.

è 2U2 ø

В общем случае

∆Uõ = kò2mπ2 Id¢xô,

где kтm2 – число коммутаций на интервале одного периода питающей сети, равное числу пульсаций выпрямленного напряжения на интервале одного периода питающей сети;

хф –индуктивноесопротивлениерассеянияобмоткифазытрансфор- матора и фазы питающей сети, приведенное ко вторичной обмотке.

Примечание. Для двойной трехфазной схемы выпрямления с уравнительным реактором следует принять ток Id′ = Id/2, а kтm2 = 3, в остальных схемах Id′ = Id и kтm2 = 6.

Таким образом, для трехфазной мостовой и кольцевой схем

∆Uõ = 26π Idxô = 3π Idxô,

101

а для двойной трехфазной схемы с уравнительным реактором

∆Uõ = 23π I2d xô = 43π Idxô.

Обратим внимание, что для выполнения расчетов падений напряжений UR и Uх необходимо знать параметры трансформатора

Rтр и хф.

Падение напряжения на активном сопротивлении обмотки дрос-

Падение напряжения на активном сопротивлении проводов, соединяющих выпрямитель с нагрузкой, определим, воспользовав-

где ρ= 0,0175 Ом · мм2/м – удельное сопротивление меди, из которой выполнены соединительные провода;

j – плотность тока в соединительных проводах. Для дальнейших расчетов можно принять j = 2 А/мм2.

∆Uø =2×4×0,0175×2=0,28 Â.

∆URL/Ud,%

10

1,0

0,1

0,02 0,1 0,2 0,5 1 2 5 10 20 50 100 Pd, êÂò 0,05

Рис. 29. Зависимость относительного падения напряжения

в сглаживающем дросселе от мощности нагрузки выпрямителя Pd

102

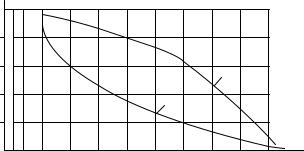
Далее определим активное и индуктивное сопротивления рассеяния обмотки трансформатора, воспользовавшись методикой, изложенной в работе [3].

В соответствии с этой методикой активное сопротивление обмотки трансформатора, приведенное ко вторичной стороне:

где m2 – число вторичных обмоток; E2 – ЭДС фазы вторичной обмотки;

екз % – напряжение короткого замыкания трансформатора; cosϕкз – коэффициент мощности короткого замыкания транс-

форматора;

Sтр – расчетная мощность трансформатора.

Зависимости екз% = f(Sтр) и cosϕкз = f(Sтр) и приведены на рис. 30 [3].

Индуктивное сопротивление рассеяния трансформатора хф определим после расчета Rтр и определения угла ϕкз = arccosϕкз, а cosϕкз определим по графику cosϕкз = f(Sтр), приведенному на рис. 30:

хф = Rтрtgϕкз.

103

Расчет в первом приближении напряжения холостого хода выпрямителя

Для расчета Ud хх достоверно известны четыре параметра:

–номинальное напряжение нагрузки UdN = 7,8 B;

–падение напряжения на открытом вентиле ∆Uв.пр = 0,83 В;

–падение напряжения на активном сопротивлении проводов, соединяющих выпрямитель с нагрузкой, ∆Uш = 0,28 В;

–падение напряжения на активном сопротивлении обмотки дрос-

селя ∆URL = 0,1 В.

Остальными падениями напряжения следует задаться.

Примем падение напряжения на активном сопротивлении обмоток трансформатора ∆UR ф = 0,1UdN = 0,8 В.

Падение напряжения от коммутации ∆Uх = 0,05UdN = 0,4 В. Таким образом, напряжение холостого хода выпрямителя со-

ставит

Ud хх = 7,8 + 2 · 0,83 + 0,8 + 0,4 + 0,1 = 11 В.

4.4. Определение расчетной мощности трансформатора

Определим в первом приближении расчетное значение мощности цепи постоянного тока выпрямителя Pd0:

Ðd0 =Ud õõIdN;

Pd0 = 11 · 2500 = 27 500 Вт.

Примем в первом приближении расчетную мощность трансформатора

Sòð =æçççèSPòð ö÷÷÷÷øPd0 =1,05×27 500=28 888 Âò, d

где Sтр/Рd – коэффициент типовой (расчетной) мощности трансформатора (см. табл. 4).

По графикам, приведенным на рис. 29, определим напряжение короткого замыкания екз% и коэффициент мощности короткого замыкания cosϕкз.

Для трансформатора, мощность которого примерно равна 29 000 Вт,

екз% = 5,2 %, а cosϕкз = 0,515.

Определим в первом приближении ЭДС холостого хода вторичной обмотки Е2.

104

Для определения Е2 следует учесть коэффициент сети kc, который учитывает отклонение сетевого напряжения от номинального значения:

kc = (Uc N – Uc)/Uc N = 1 – 0,15 = 0,85,

а также минимальное значение угла регулирования αmin. Обычно величина αmin принимается в пределах 8–10°. Примем αmin = 10°. Пока трансформатор и дроссель не выбраны, следует задаться падениями напряжения на них.

С учетом принятых уточнений

Активное сопротивление обмотки трансформатора, приведенное ко вторичной стороне:

Поскольку выпрямитель питается от промышленной сети (сети бесконечно большой мощности), индуктивным сопротивлением питающей сети можно пренебречь, поэтому в дальнейших расчетах принимаем

хф = хтр = 1,45 · 10–4 Ом.

Падение напряжения от явления коммутации для трехфазной мостовой схемы

∆Uх = (6/2ϕ)Idхф = 0,955 · 2500 · 1,45 · 10–4 = 0,35 В.

Для трехфазной мостовой схемы выпрямления эквивалентное активное сопротивление фазы

Rô.ý =2Rô =2(Ròð +Râ.ä) =2×(0,87+1) ×10-4 =3,74×10-4 Îì.

105

Падение напряжения на активных сопротивлениях обмоток трансформатора и динамических сопротивлениях тиристоров

∆UR = IdNRô.ý =2500×3,74×10-4 =0,935 Â.

Падение напряжения на активных сопротивлениях обмоток трансформатора и динамических сопротивлениях тиристоров c учетом угла коммутации:

∆URγ = 3π IdRôæççè23π -2γö÷÷÷ø=

=0,955×2500×1,87×10-4 ×1,936=0,87 Â.

Определим величину напряжения холостого хода выпрямителя с учетом рассчитанных падений напряжения:

Ud xx =UdN +∆Uâ.ïð +∆URγ +∆Uõ +∆URL +∆Uïð =

=7,8+1,66+0,87+0,35+0,1+0,28=11,06 Â.

Уточненное значение напряжения холостого хода выпрямителя практически совпадает с принятым ранее значением, и проводить корректировку расчетов по расчету мощности трансформатора и падений напряжения на элементах схемы не требуется.

4.5. Расчет потерь мощности и КПД выпрямителя

Потери мощности на активных сопротивлениях обмоток трансформатора

∆Ðýë =3I22 ×2Ròð =3×20412 ×2×0,87×10-4 =2174 Âò.

Действующее значение тока вторичной обмотки трансформатора без учета влияния коммутации

Действующее значение тока вентиля

106

Потери мощности в тиристорах

∆Ðâ =Id ×2∆Uâ.ïð +Iâ.ä2 ×2Râ.ä =

=2500×2×0,83+14432 ×2×1×10-4 =4566 Âò.

Потери мощности на активном сопротивлении проводов, соединяющих выпрямитель с нагрузкой:

∆Ðø = ∆UøIdN =0,28×2500=700 Âò.

Потери мощности на активном сопротивлении обмотки сглаживающего дросселя

∆ÐRL =∆URLIdN =0,1×2500=250 Âò.

Сумма потерь мощности

å∆Ð=∆Ðýë +∆Ðâ +∆Ðø +∆ÐRL =

=2174+4556+700+250=7680 Âò.

Коэффициент полезного действия выпрямителя

η= ÐdN = 7,8×2500 =0,717. PdN +å∆P 19 500+7680

Результаты расчета сведены в расчетный формуляр (табл. 13).

Таблица 13

Расчетный формуляр

107

108

Примечание. Напряжение Ud xx, рассчитанное в п. 14, является уточненным значением Ud xx, рассчитанным в первом приближении в п. 5.

109

Проанализируем полученные результаты.

Достаточно низкое значение КПД выпрямителя объясняется в первую очередь относительно большими, по сравнению с остальными, потерями мощности в вентилях выпрямителя.

Наименьшая расчетная мощность трансформатора требуется для трехфазного мостового выпрямителя, Sтр = 29 кВ · А. Для остальных двух схем расчетная мощность трансформатора больше: так, для кольцевой схемы выпрямления расчетная мощность трансформатора больше почти на 16%.

Потери мощности наибольшие – в трехфазной мостовой схеме выпрямления, и, следовательно, КПД этой схемы меньше.

Наибольший КПД – у дважды трехфазной схемы выпрямления. Отметим важное обстоятельство, которое оказывает существенное влияние на потери мощности и КПД: это низкое выходное напряжение выпрямителя и сильноточная нагрузка. Именно этим обстоятельством и объясняется сравнительно невысокое значение КПД рассмотренных схем выпрямления и самое низкое значение КПД у трехфазного мостового выпрямителя, у которого ток нагруз-

ки проходит через два последовательно соединенных тиристора. Из трех рассмотренных схем выпрямления следует отдать пред-

почтение кольцевой схеме выпрямления как имеющей достаточно высокий КПД и не имеющей уравнительного реактора. Из-за низкого значения напряжения нагрузки, равного 7,8 В, для всех трех схем выпрямления приходится выбирать тиристоры на одно и то же напряжение 100 В, поэтому плохое использование тиристоров по напряжению в кольцевой схеме выпрямления не приводит к увеличению стоимости этого выпрямителя по сравнению с трехфазной мостовой схемой.

Наличие уравнительного реактора в дважды трехфазной схеме выпрямления является очевидным недостатком, увеличивает массу, габариты и стоимость.

4.6. Расчет сглаживающего фильтра

Для расчета индуктивности сглаживающего дросселя Ld необходимо определить гармонический состав выпрямленного напряжения управляемого выпрямителя.

Амплитуда высшей гармоники порядка k определяется по формуле [2]

110