ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ

Информатика

Методические указания к выполнению лабораторных работ

Санкт-Петербург 2014

2

Лабораторная работа №1. Введение в MATLAB

Краткая характеристика MATLAB

MATLAB (сокращение от англ. «Matrix Laboratory») – это пакет прикладных программ для решения задач технических вычислений и одноименный язык программирования, используемый в этом пакете.

Система MATLAB предлагается разработчиками (корпорация The MathWorks, Inc.) как лидирующий на рынке, в первую очередь на предприятиях военно-промышленного комплекса, в энергетике, в аэрокосмической отрасли и в автомобиле строении язык программирования высокого уровня для технических вычислений, расширяемый большим числом пакетов прикладных программ – расширений. Самым известным из них стало расширение Simulink, обеспечивающее блочное имитационное моделирование различных систем и устройств. Но и без пакетов расширения MATLAB представляет собой мощную операционную среду для выполнения огромного числа математических и научно технических расчетов и вычислений и создания пользователями своих пакетов расширения и библиотек процедур и функций.

Робота в среде MATLAB может осуществляться в двух режимах:

•в интерактивном режиме, когда вычисления осуществляются сразу после набора очередного оператора или команды MATLAB; при этом значение результатов вычисления могут присваиваться некоторым переменным, или результаты получаются непосредственно, без присваивания (как в обычных калькуляторах);

•путем вызова имени программы, написанной на языке MATLAB, предварительно составленной и записанной на диске, которая содержит все необходимые команды, обеспечивающие ввод данных, организацию вычислений и вывод результатов на экран (программный режим).

Именно с интерактивного режима мы начнем работу в MATLAB.

Описание интерфейса MATLAB

После запуска можно будет увидеть следующее окно системы MATLAB, представленное на рисунке 1.

3

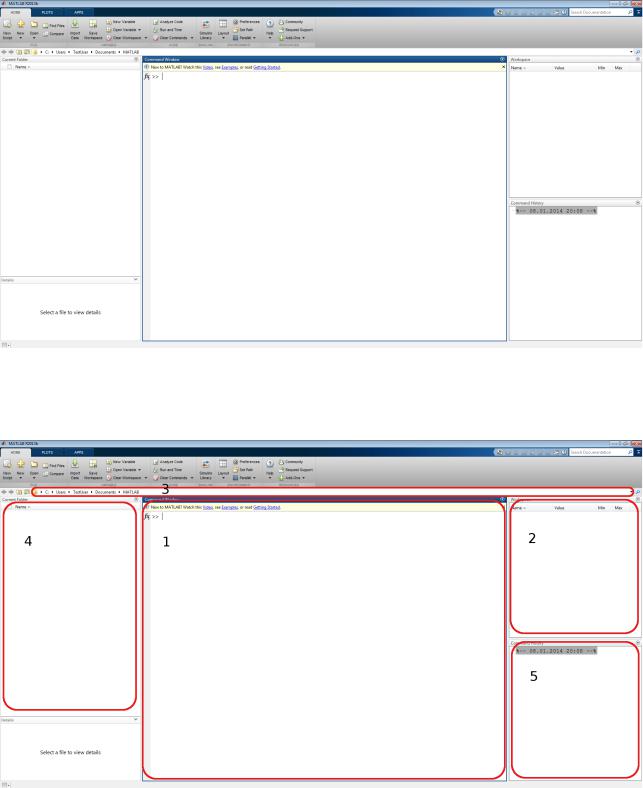
Рисунок 1. Окно системы MATLAB R2013b после запуска

Далее рассмотрим основные элементы графического интерфейса MATLAB, отмеченные на рисунке 2, и кратко опишем из назначение.

Рисунок 2. Основные элементы пользовательского интерфейса MATLAB Основные элементы интерфейса MATLAB:

1.Командное окно, предназначенное для интерактивной работы в MATLAB;

2.Рабочая область, в которой отображаются текущие переменные;

3.Рабочий каталог, где содержатся пользовательские скрипты и функции;

4

4.Содержимое рабочего каталога;

5.История команд введенных в командное окно.

Работа с MATLAB в режиме командной строки

Простые вычисления

Рассмотрев основные элементы интерфейса прейдем непосредственно к работе с

>>3 * 2 ^ 2 - 4 * 2 + 10

инажать Enter. Символом >>, как и в MATLAB, будем в дальнейшем обозначать

приглашение к вводу. После нажатия Enter в ответ MATLAB выведет: ans =

представленного выражения необходимо будет использовать функции MATLAB sin, cos и константу pi (технически так же является функцией). Так же отметим, что все тригонометрические функции в MATLAB принимают значения угла в радианах. Теперь вычислим данное выражение:

>> cos(pi/2)*cos(-pi/6)-sin(pi/2)*sin(-pi/6)

ans =

0.5000

Объявление переменных

Для создание переменной в MATLAB необходимо просто присвоить ей значение с помощью оператора присваивания «=». Например создадим переменную x:

>> x = 2

x =

2

В данном случае, когда MATLAB встречает имя новой переменной, он автоматически

5

создает новую переменную и выделяет для нее нужный объем памяти. Если данная переменная уже существовала, то он изменит ее значение, и при необходимости выделит дополнительную память.

Тип созданной переменной определяется типом присваиваемого значения. В данном примере переменная x будет иметь тип double (число с плавающей точкой двойной точности), так как все числа по умолчанию в MATLAB имеют тип double.

Теперь немного остановимся на именах переменных. Имя переменной может содержать:

•латинские буквы (A-Z и a-z)

•цифры (0-9)

•знак подчеркивания (_)

При этом имя обязательно должно начинаться с буквы и не должно совпадать с ключевым словом MATLAB. Так же необходимо учитывать, что MATLAB чувствителен к регистру, и поэтому будет считать переменные x и X разными. В таблице 1 приведены примеры допустимых и недопустимых имен переменных:

Таблица 1: Примеры имен переменных

недопустимые имена переменных

6x

>>x = 2;

>>y = 3 * x ^ 2 - 4 * x + 10;

Отметим, что в данном случае после выражения был поставлен символ «;». Данный символ подавляет вывод в консоль значения вычисленного выражения или результата присвоенного переменной. Поэтому для того чтобы вывести значение данной переменной достаточно просто ввести ее имя:

>> y

y =

14

Теперь произведем аналогичные действия для второго примера:

>>a = pi / 2;

>>b = - pi / 6;

6

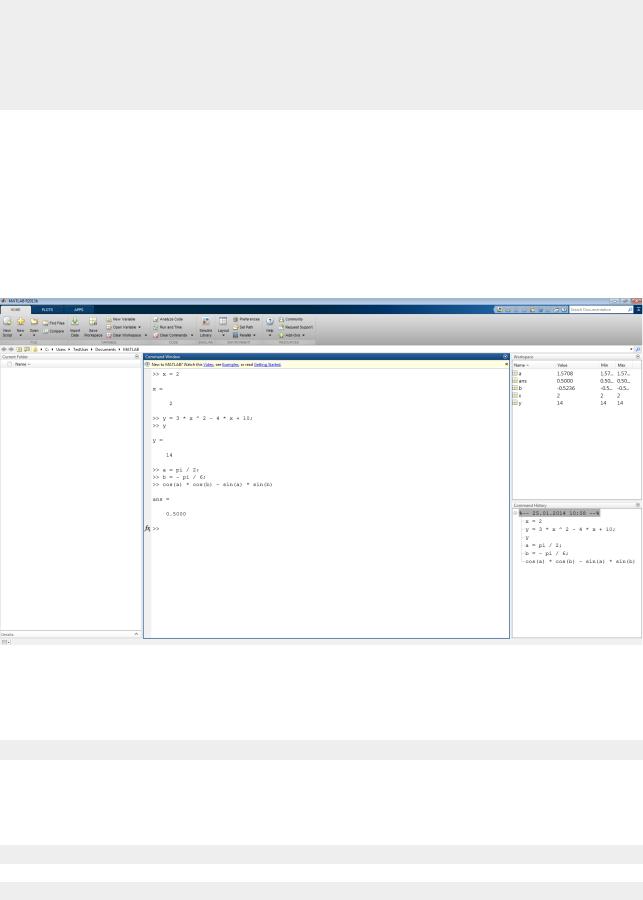
>> cos(a) * cos(b) - sin(a) * sin(b)

ans =

0.5000

Отметим, что в приведенном выше примере, результат вычисления выражения не были присвоены какой либо переменной. В таких случаях MATLAB присваивает результаты вычислений переменной ans.

Удаление созданных переменных

Все созданные переменные и их значения можно отображаются в окне workspace (рисунок 3).

Рисунок 3. Текущие переменные

Для удаления переменных в MATLAB из рабочей области предусмотрена команда clear. Так для удаления переменной x нужно ввести:

>> clear x

Для удаления нескольких переменных сразу необходимо после команды сlear перечислить имена переменных через пробел. Если нужно удалить сразу все переменные, то нужно ввести команду clear без аргументов:

>> clear

Для очистки командного окна нужно ввести следующую команду:

>> clc

7

Создание матриц и векторов

Почти все переменные в MATLAB являются матрицами, даже скалярные значения, созданные в примерах выше, считаются матрицами размером 1 на 1. Матрицы в MATLAB являются важнейшим типом для данного языка, поэтому рассмотрим способы ввода матрицы

В данном случае элементы матрицы, находящиеся в одной строке, разделяют пробелами, а строки разделяются символом «;». Так же элементы находящиеся в одной строке можно разделить с помощью запятых:

>> A = [1.2, 2.4, 3.1; 4.3, 5.3, 6.4]

A =

Следует отметить, что дробная часть числа отделяется от целой точкой, а не запятой. Аналогичным образом можно создать векторы:

>> x = [1 2 3]

x =

1 2 3

>> y = [1; 2; 3]

y =

1

2

3

В данном случае x это вектор-строка, а y вектор-столбец. Отличия вектора-столбца от вектора-строки проявляются при использовании матричных операций и использовании функций.

8

Рассмотрим еще один важный способ задания вектора-строки — оператор двоеточия «:». Например:

>> 1:10

В данном случае значение 10 не содержится в векторе, так как оно задает лишь максимальное значение (или минимальное, при отрицательном шаге), которое будет содержаться в векторе.

Шаг так же может быть отрицательным:

Поэлементные операции над матрицами

Рассмотрим поэлементные операции над матрицами/векторами, которые понадобятся в дальнейшем для построения графиков.

Многие функции MATLAB могут работать с матрицами и векторами. Рассмотрим в качестве примера функцию sin:

>> x = 0 : pi/6 : pi

x =

3.1416

>> sin(x)

ans =

0.0000

9

Результат данных вычислений является вектор такого же размера, что и входной аргумент функции sin, содержащий значения синуса элементов вектора x.

Так же можно производить поэлементные операции сложения, вычитания, умножения, деления и возведения в степень для матриц/векторов одинаковой размерности. Например:

>>x = [1 2 3];

>>y = [3 2 1];

>>x + y

ans =

4 4 4

>> x - y

ans =

-2 0 2

>> x .* y

ans =

3 4 3

>> x ./ y

ans =

0.3333 1.0000 3.0000

>> x .^ y

ans =

1 4 3

Однако если попытаться поэлементно умножить матрицы разного размера, то получим ошибку:

>>x = [1 2 3];

>>y = [3; 2; 1];

>>x .* y

Error using .*

Matrix dimensions must agree.

Отметим, что для поэлементного умножения, деления и возведения в степень необходимо перед операцией ставить точку: «.*», «./», «.^», иначе будут применяться

10