Отчёт по л.р. 1 в MathCAD
.rtfВариант 1.
Задание 1.
Задавая x, y, z, найти значение выражения:
.
Решение.
Используем программу Mathcad. Зададим x, y, z, предварительно задав функцию:
При x=1, y=2, z=1:
.
При x=1.5, y=3, z=2:
.
При x=0, y=-5, z=20:
.
Задание 2.
Вычислить значение функции:
для
x: -3,5; 1,5; 3,2; 5;
;
;
log410
.
Решение.
Используем программу Mathcad. Зададим функцию:
.
Вычислим значения функции.
При
x=-3.5 значение
.
При
x=1.5 значение
.
При
x=3.2 значение
.
При
x=5 значение
.
При
x=
значение
.
При
x=
значение
.
Далее используем для логарифма формулу перехода к другому основанию:
при
x=
значение
.
При
x=sin(8) значение
.
Задание 3.
Для
вычисления значения выражения
построить функцию, которая бы возвращала
текст "not defined" при недопустимых
значениях переменной x. Выполнить
вычисления для x: -4; -2; 0; 1,5; 5.
Решение.
Используем
программу Mathcad. Выражение имеет смысл
тогда, когда подкоренное выражение
больше или равно 0, причём x не может
принимать значение, равное -2. Рассуждая
так, можно получить следующую логическую
переменную:
.
Зададим функцию:
.
Вычислим значения функции. При x=-4:
.
При
x=-2:
.
При
x=0:
.
При
x=1,5:
.
При
x=5:
.
Задание 4.
Из круглой жестянки по простой технологии изготавливается пожарное ведро: вырезается сектор, затем полученная выкройка сворачивается в конус, а шов сваривается. Требуется построить функцию V(R,α), с помощью которой можно рассчитать объём ведра, если известны радиус жестянки R (см) и угол вырезки α (градусы). Выполнить расчёт для следующих значений радиуса заготовки и угла:
Решение.
Используем
программу Mathcad. Площадь боковой
поверхности конуса s=πrL,
где r-радиус основания конуса, L-образующая
конуса, равная радиусу жестянки (L=R).
Эту формулу можно записать иначе: s=
,
где β=
,
где α
в градусах. Объём конуса: V=
,
где h-высота конуса. Так как h=
,
а радиус цилиндра можно выразить через
радиус жестянки как
,
то формулу объёма конуса можно записать
так:
.
.
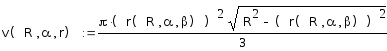Теперь
можно выполнить расчёт. При R=50 см и
α=120°
:
,
(
).
При
R=65 см и α=
радиан или
(градусов):
(
).
При
R=0,74 м = 74 см и α=
радиан или
(градусов):
(
).
При
R=0,85 м = 85 см и α=180°
:
(
).
Задание 5.
Чему равно общее сопротивление участка электрической цепи, изображенного на рисунке ниже, если известно, что R1=3 Ом, R2=12 Ом, R3=6 Ом?
Решение.
При последовательном соединении резистивных элементов общее сопротивление участка цепи равно сумме сопротивлений отдельных резистивных элементов, при параллельном соединении общая проводимость участка цепи равна сумме проводимостей каждого элемента: R131=R1+R1+R3, G3131=G131+G3, G23131=G2+G3131, R=R1+R23131. Используем программу Mathcad:
.
Найдём искомое сопротивление:
(Ом).
Ответ: 6 Ом.