4.3. Чувствительность давления

Поперечное сечение капсулы ощущения может быть смоделировано как тонкостенный луч. Поэтому, резонансная частота может быть выражена как [12]

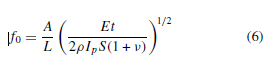
где L - длина (ширина) квадратной мембраны, A - скрытая область, E - Модуль Юнга эластичности кремния, t - мембранная толщина, Ip - полярное, момент инерции поперечного сечения об оси скрученности, ρ - плотность кремния, S - периметр скрытой области, и ν - Коэффициент поперечного сжатия для кремния. Чувствительность давления может быть найдена, беря логарифм уравнения (6) и дифференцируясь относительно перепада давления. Получающееся нелинейное выражение во власти термина, связанного с поперечным, резонатора, и имеет форму [11]

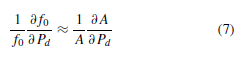
где A является площадью поперечного сечения капсулы ощущения, и Фунт является перепадом давления через мембрану ощущения. Термин 1/A больше для меньшей поперечной краткой области, в то время как изменение в площади поперечного сечения для разнообразия в давлении равное для структуры с большой или маленькой площадью поперечного сечения. Поэтому, чтобы увеличить чувствительность давления этого устройства, по сравнению с ранее представленным датчиком, толщина мембран капсулы ощущения была уменьшена (приводящий к большему ∂A). Мембраны были также расположены (то есть приближены вместе), производство меньшей внутренней поперечной капсулы, который одобряет чрезвычайно давление чувствительная структура (меньший A). Этот расположенный дизайн также уменьшает область, способствующую демпфированию сжатого фильма. Рисунок 5 сравнивает предыдущий дизайн датчика давления с улучшенным, больше давления чувствительный дизайн, используемый в текущем датчике давления.

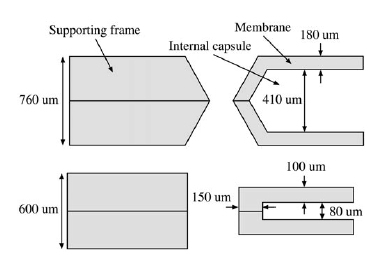
Рисунок 5. Поперечное представление поддержки развивается и внешняя часть капсулы замера давления для ранее представленного датчика [4] (a) и новый улучшенный дизайн (b).

4.4. Температурная зависимость

Поскольку температура окружающей среды изменяется, резонансная частота изменений датчика. Это изменение может быть приписано двум факторам. Во-первых, если мы примем увеличения температуры окружающей среды, то газ в герметизации расширится, и мембраны будут выпирать, внутрь приводя к менее жесткой структуре (уменьшающий резонансную частоту). Однако, так как давление во впадине герметизации очень низкое (приблизительно 1 mbar [7]), этот эффект незначительный. Во-вторых, поскольку температура увеличивается, Модуль Юнга уменьшений эластичности и кремния становится более гибким (уменьшения резонансной частоты). Так как эффект из-за Модуля Юнга эластичности доминирует, можно попытаться дать компенсацию за этот эффект, выбирая измерения, которые отменят E в уравнении (2) [5]. Однако, так как датчик является базируемой формой, и Ip и S также зависят от Модуля Юнга эластичности. После некоторого математического анализа мы можем прийти к заключению, что это, математически, не возможно к полностью температуре, дают компенсацию, выбирая соответствующие измерения. Однако, проектирование капсулы ощущения с тонкими мембранами, имеющими большой диаметр, имеет тенденцию одобрять температурную компенсацию [11].