-
Однородные системы уравнений. Ранг матрицы и существование нетривиального решения.
Линейное уравнение называется однородным, если его свободный член равен нулю, и неоднородным в противном случае. Система, состоящая из однородных уравнений, называется однородной и имеет общий вид:
Очевидно, что всякая однородная система совместна и имеет нулевое (тривиальное) решение. Поэтому применительно к однородным системам линейных уравнений часто приходится искать ответ на вопрос о существовании ненулевых решений. Ответ на этот вопрос можно сформулировать в виде следующей теоремы.
Теорема. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных.
Доказательство:
Допустим, система, ранг которой равен,
имеет ненулевое решение. Очевидно,
что 
не
превосходит 
.
В случае 
система
имеет единственное решение. Поскольку
система однородных линейных уравнений
всегда имеет нулевое решение, то именно
нулевое решение и будет этим единственным
решением. Таким образом, ненулевые
решения возможны только при 
.
Следствие 1: Однородная система уравнений, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение.
Доказательство:
Если у системы уравнений 
,
то ранг 
системы
не превышает числа уравнений 
,
т.е. 
.
Таким образом, выполняется условие 
и,
значит, система имеет ненулевое решение.
Следствие
2: Однородная система 
уравнений
с 
неизвестными
имеет ненулевое решение тогда и только
тогда, когда ее определитель равен нулю.
Доказательство:
Допустим, система 
линейных
однородных уравнений, матрица которой 
с
определителем 
,
имеет ненулевое решение. Тогда по
доказанной теореме 
,
а это значит, что матрица 
вырожденная,
т.е. 
.
Разрешенные системы линейных уравнений
Переменная 
называется
разрешенной, если какое-нибудь уравнение
системы содержит 
с
коэффициентом, равным единице, а во все
остальные уравнения системы переменная 
не
входит, т.е. входит с коэффициентом,
равным нулю.
Однородная система линейных уравнений AX = 0 всегда совместна. Она имеет нетривиальные (ненулевые) решения, если r = rank A < n.
Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:
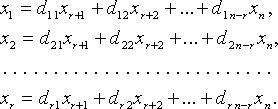
Тогда n - r линейно независимыми вектор-решениями будут:
а
любое другое решение является их линейной
комбинацией. Вектор-решения 
образуют
нормированную фундаментальную систему.
В
линейном пространстве 
множество
решений однородной системы линейных
уравнений образует подпространство
размерности n
- r; 
-
базис этого подпространства.
-
Структура общего решения однородной системы уравнений.
AX=0 (1)
Если Х1 Хn – решение системы, то любая их линейная комбинация , тоже решение этой системы уравнений.
АХ1 = 0 АХ2 = 0 AXn = 0
A(
1
X1
+
2
X2
+ … +
n
Xn)=
1
A X1+
2
A X2
+…+
n
A Xn
= 0
(то что в скобках) – линейная комбинация
Теорема: Пусть r = rank A<n , тогда существует (n-r) линейно независимое решение системы (1). А все остальные решения представляются, как их линейная комбинация.
Определение:
Набор
линейно-независимых решений называется
набором фундаме6нтальных решений системы
(1).
АХ=0 Х1
А – матричный коэффициент Х= ...
А – m x n – матрица Хn
r = rank A<n
Тогда:
-
Существует (n – r) решение системы (1)
-
Все остальные решения являются линейными коэффициентами (n – r) решений
Определение: Эти решения называются функцией решений
Доказательство:
U1 U2 . . . Un – Столбцы матрицы А
X1U1 + x2U2 +. . . + xnUn = 0
По теореме о базисном миноре столбец Uk, является линейной комбинацией базисных столбцов.
Uk
=
1U1
+
2U2
+ . . . +
nUn
Uk
–
1U1
–
2U2
– . . . –
nUn
= 0
Сравним
строчку 1, со строкой 1. Числа (-
1
2
…
r,
0 . . . 1, 0)
1
– k
Xk
= -
1
-
2
-
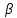r
- столбец решений
0 Покажем, что столбцы независимы.
1
Пусть существуют числа:
r+1,
r+2
. . .
n
, такие что
0
r+1
Xr+1
+
r+2
Xr+2
+ . . . +
n
Xn
= 0 (2)
}r
r+1
= 0 =>
r+1
=
r+2
= . . . =
n
= 0
r+2
Равенство
(2) может выполнятся, только если вес
= 0, значит столбцы Хк
– линейна независима
Доказательство 2: Пусть z – столбец решений системы (1)
Z = Z1
Z2
Z r+1
. . .
Zn
Y = Z – Z r+1 X r+1 – Z r+2 X r+2 - . . . – Zn Xn
Все столбцы Z и Х, решение наших уравнений, значит У тоже является решением уравнений
Y= Y1
Y2
Yn Y1U1 +Y2 U2 + . . . + Yr Ur = 0 (3)
0 r
0 r+1
Y1, Y2 – базисные столбцы нашей матрицы, линейно независимы, соотношение (3) выполняется только в 1 случае, когда все y =0 => столбец х=0 => Z = Zr+1 Xr+1 + Zr+2 Xr+2 + . . . +ZnXn (6)
Строчка (6) означает, что столбец “z” является линейной комбинацией столбцов X
Любое
решение системы (1), имеет следующий вид
: x
=
k
Xk
Фундаментальное решение – эта формула описывает общее решение однозначной системы уравнения.
– принимает решения,
которые возникали в процедуре Гауса.