33. Гипербола, ее директриссы

Гипербола.

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая чем расстояние между фокусами.

y

M(x;y)

F(-c;0) F(c;0) x

x=-a x=a

Согласно определению гиперболы │МF₁│-│MF₂│ = 2а, то есть

После упрощений, как это было при выводе уравнения эллипса, получим каноническое уравнение гиперболы:

(7)

b² = c² – a² (8)

34. Парабола

Парабола.

Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой директрисой. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается буквои Р(Р>0). Для вывода уравнения параболы выберем систему координат Оху, так чтобы ось Ох проходила через фокус F.

N M(x;y)

x=-P/2 0 x F(P\2;0) x

По определению параболы МF = MN, по формуле расстояний между двумя точками находим: отсюда получаем:

(9)

Это и есть каноническое уравнение параболы.

Пример: из уравнения (1) можно определять:

при А=С – окружность

АС>0 – эллипс

АС<0 – гипербола

АС=0 – парабола

Пример: установить вид прямой 2 –ого порядка, заданной уравнением 4х²+5у²-20х-

-30у+10=0

Решение: А=4 С=5 АС=4∙5=20>0 – следовательно это эллипс

Центр эллипса -

Пример 2: х²+10х-2у+11=0 С=0 АС=0 следовательно парабола

х²+10х-2у+11+25-25=0

(х+5)² = 2у+14

(х+5)²=2(у+7) – уравнение параболы

О(-5;7) – вершина параболы ; Р=1

35. Уравнение кривых второго порядка в полярных координатах.

Кривой второго порядка на плоскости называют множество точек (х, у) удовлетворяющие:

Ax+ 2Bxy + Cy + 2Dx + 2Ey + F = 0 (a)

Сдвиг начала координат

x=х’ +a y=y’ +b a и b const

Получаем такое же уравнение (а) только с другими коэффициентами

Поворот системы координат

X= x’cos – y’ sin

Y= x’sin + y’ cos

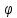
При повороте уравнение (а) остаётся, только с другими коэффиц.

Можно ли с этими процедурами упростить А?

С помощью поворота:

A(x’cos – y’sin ) + 2B(x’cos – y’sin)*(x’sin + y’cos+ C(x’sin + y’cos²+. . . =

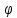x’y’(-2Acossin + 2cossin+ 2B(cos2 – sin2) + . . . = x’y’[sin²(C-A)+2Bcos²]+. . .

нужно обнулить это уравнение

(C – A)sin2 = 2B cos tg 2 =

Tg принимает любое значение, поэтому это уравнение имеет решение при любой кривой части, следовательно, Bxy можно устранить с помощью поворота

Ax² +Cy² + 2Dx + 2Ey +F = 0 (b)

Если АС 0 то можно устранить Е и С

A(x + 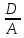)² + C(y + )² +F² = 0

Можно написать: x’ = x +

y’ = y + сдвиг начала системы координат

Ax2 + Cy2+ F = 0 (c)

A,C,F – одного знака, тогда + = -1 F переношу направо и делю на F, получаем уравнение мнимого элипса