
- •10. Алгоритм rsa.
- •11. Алгоритмы быстрого умножения чисел
- •12. Алгоритм Тоома Кука
- •13. Алгоритм быстрого деления.
- •14. Тесты простоты. Числа Камайкла
- •15. Алгоритмы факторизации. Метод Полларда
- •16. Система Мак-Элиса
- •19. Атака на систему Мак-Элиса
- •20. Построение конечной проективной плоскости
- •21. Код для защиты от подлога
- •Алгоритм
- •24. Алгоритм Евклида
- •25. Теорема Эйлера
- •26. Китайская теорема об остатках
- •Операции
- •Алгоритм Гаусса
- •Алгоритм Гарнера
13. Алгоритм быстрого деления.
? Что-то как умножение? о_О
14. Тесты простоты. Числа Камайкла
Тест простоты — алгоритм, который по заданному натуральному числу определяет, является ли это число простым. Различают детерминированные и вероятностные тесты.
Тесты Простоты:
- Проверка делением (делить на всё подряд)
- Тест основанный на малой Теореме Ферма.
Если
n —
простое число, то оно удовлетворяет
сравнению
![]() для
любогоa.
для
любогоa.
Выполнение
сравнения
![]() является
необходимым, но не достаточным признаком
простоты числа. То есть если хотя бы для
одногоa
является
необходимым, но не достаточным признаком
простоты числа. То есть если хотя бы для
одногоa
![]() ,
то числоn
составное, в противном случае ничего
сказать нельзя, хотя вероятность того,
что число является простым увеличивается.
Если для составного числа n
выполняется сравнение
,
то числоn
составное, в противном случае ничего
сказать нельзя, хотя вероятность того,
что число является простым увеличивается.
Если для составного числа n
выполняется сравнение
![]() ,
то числоn
называют псевдопростым по базе a.
При проверке числа на простоту тестом
Ферма выбирают несколько чисел a.
Чем больше количество a,
для которых
,
то числоn
называют псевдопростым по базе a.
При проверке числа на простоту тестом
Ферма выбирают несколько чисел a.
Чем больше количество a,
для которых
![]() ,
тем больше вероятность, что числоn
простое.
,
тем больше вероятность, что числоn
простое.
- Числа Кармайкла
Пусть n-нечетное составное. Тогда
А)
если
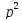 |n,
p>1,
то n
не является числом Кармайкла
|n,
p>1,
то n
не является числом Кармайкла
Б)
если n=p1,p2…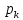 ,
,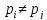 , тоn
число
Кармайкла в том и только в том случае,
когда при всех I
выполнено
условие (
, тоn
число
Кармайкла в том и только в том случае,
когда при всех I
выполнено
условие (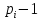 )(n-1)
)(n-1)
В)
если n=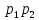 …
…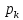 ,
,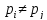 число
Кармайкла, тоk≥3
число
Кармайкла, тоk≥3
- тест Соловея-Штрассена
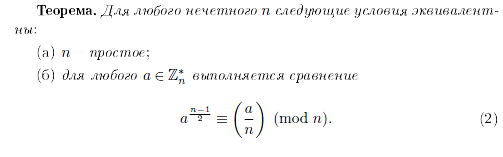
- тест Миллера-Рабина

- символ Лежандра
- Символ Якоби
15. Алгоритмы факторизации. Метод Полларда
Задача факторизации - разложение на множители.
ρ - Метод Полларда.
С
помощью этого метода было впервые
факторизовано число Ферма . Впервые
этот алгоритм был предложен Дж. Поллардом
в 1975 г. Суть его заключается в следующем:
![]()
1.
Выбираем отображение , где - кольцо
вычетов по модулю n. В качестве функции
обычно берут полиномы степени ≥2
(например ).
![]()
![]()
![]()
![]()
2.
Выбираем некоторое число и строим
рекурсивную последовательность по
следующему принципу
![]()
![]()
![]() .
.
3.
Для некоторых номеров i и j вычисляем
![]() .
Если или
.
Если или![]()
![]() ,
то рассматриваем другую пару
,
то рассматриваем другую пару![]() .
Если
.
Если![]() ,
то d – делитель числа n.
,
то d – делитель числа n.
Как
видим, алгоритм может оказаться довольно
громоздким из-за большого количества
пар . Эта проблема решаема с помощью
некоторых способов выбора номеров i и
j. Рассмотрим некоторые из них:
![]()
1.
, т.е.
![]()
![]()
2.
Если j удовлетворяет условию , то берут
![]()
![]()
Если
окажется, что алгоритм не нашел делителя,
то можно попробовать другие функции f,
например , где с – некоторая константа.
![]()
Сложность
этого алгоритма оценивается, как
![]() битовых
операций. Существует теорема, которая
формулируется так: Пусть n – составное
число,
битовых
операций. Существует теорема, которая
формулируется так: Пусть n – составное
число,![]() вероятность
того, что метод Полларда не сможет найти
нетривиальный делитель n за время
вероятность
того, что метод Полларда не сможет найти
нетривиальный делитель n за время![]() не
превышает величину .
не
превышает величину .![]()
ρ - Метод Полларда обычно используется для нахождения небольших делителей числа n.
(P-1)-метод Полларда.
Прежде
чем начать рассмотрение этого алгоритма
введем определение: будем говорить, что
число k является B-степенно-гладким для
некоторого B>0, если : m – простое и
является делителем числа k, выполнено
условие
![]()
![]() ,
где
,
где![]() -
наибольшее число такое, что
-
наибольшее число такое, что![]()
![]() делит
k.
делит
k.
Теперь непосредственно сам алгоритм:
1.
Исходя из возможностей нашей вычислительной
машины, выбираем границу гладкости B.
Обычно B~.
![]()
2.
Выбираем произвольное целое число a,
удовлетворяющее условию
![]() ,
и вычисляем . Если
,
и вычисляем . Если![]()
![]() ,
то d – искомый делитель.
,
то d – искомый делитель.
3.
Строим таблицу всех простых чисел
![]() и
для каждого такого числа находим
и
для каждого такого числа находим![]()
![]() ,
т.е. .
,
т.е. .![]()
4.
Вычисляем
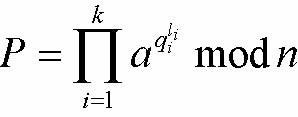
5.
Находим
![]() .
Если
.
Если![]() ,
то d – искомый делитель, иначе алгоритм
не смог найти делитель. В этом случае
можно взять другое основание a или
границу гладкости.
,
то d – искомый делитель, иначе алгоритм
не смог найти делитель. В этом случае
можно взять другое основание a или
границу гладкости.
Оценка
сложности этого метода в худшем случае
составляет
![]() арифметических
операций. Однако в некоторых случаях
этот алгоритм может довольно быстро
найти делитель n.
арифметических
операций. Однако в некоторых случаях
этот алгоритм может довольно быстро
найти делитель n.
