61. Методы измерений параметров частотно-модулированных сигналов. Измерение девиации частоты.

Методы измерения девиации частоты

• частотные на расстроенных контурах;

• импульсные частотные;

• частотные на основе линии задержки и фазового дискриминатора

• спектральный метод

Импульсные частотные детекторы (счетные детекторы )

В основе работы детектора лежит принцип преобразования ЧМ сигнала в последовательность видеоимпульсов со строго заданными амплитудой и длительностью, частота следования которых соответствует закону модуляции

Частотные детекторы на основе ЛЗ и фазового дискриминатора

Исследуемый ЧМ сигнал непосредственно и через линию задержки поступает на балансный фазовый детектор (схема сложения). Выходной НЧ сигнал детектора будет периодической функцией фазового сдвига, обусловленного введенной задержкой t.

Частотные детекторы на основе ЛЗ

Если частота входного сигнала меняется по закону:

w(t) = (w₀ + b sin W) t

то частота сигнала u(t₂)= U₂ sinwt отличается от u(t₁)=U₁sin(wt+j) на j из-за введенной задержки t. Существуют свойства таких сигналов:

U²_å = U²₁+U²₂ +2U²₁U²₂cosj = 4U²cos(j/2)

т.к. U₁=U₂=U.

Откуда находим сдвиг фазы: j = 2arccos(U_å /2)

Т. о. измерение частоты W сводится к измерению фазы j , при этом: j = b sin W t.

Спектральный метод (метод исчезающей несущей или метод нулей функции Бесселя)

основан на нахождении нуля ф-ции Бесселя нулевого порядка k=0:

u(t) = U_н× J_k (b)× sin(w_o+kW)t

U_н J₀ (b)× sinw_ot = 0

Метод заключается в изменении индекса модуляции b (путём изменения частоты: b = ω_d /W ) и регистрации по шкале анализатора спектра момента обращения в нуль спектральной составляющей J₀ (b)

Измерение индекса b методом исчезающей несущей

Увеличивая b добиваются исчезновения f₀. Так как известно b и W , то находят w_д.

Метод позволяет измерять парциальные значения коэффициента амплитудной модуляции М_n и коэффициента гармоник К_Г.

Метод основан на линейной связи спектра огибающей с боковыми полосами спектра AM колебания.

Сигналы w₀ ± w_д и w_г поступают на смеситель, а с него разность этих сигналов – на осциллограф. При равенстве сигналов: w₀ ± w_д = w_г , на экране появится горизонтальный участок . Зная w_г и w₀ получим w_д .

Схема измерителя модуляции СК3-46

Исследуемый сигнал в диапазоне частот 4-1000 МГц подается на вход ВЧ преобразователя частоты, где преобразуется в сигнал промежуточной частоты, равной 1 или 2 МГц, в зависимости от значения измеряемой девиации, фильтруется от остатков сигнала гетеродина и побочных продуктов преобразования и затем поступает в тракт ПЧ1.

Сигнал в диапазоне частот 0,1–4 МГц поступает на входные фильтры (на схеме не показанные) и затем непосредственно в тракт ПЧ2 прибора.

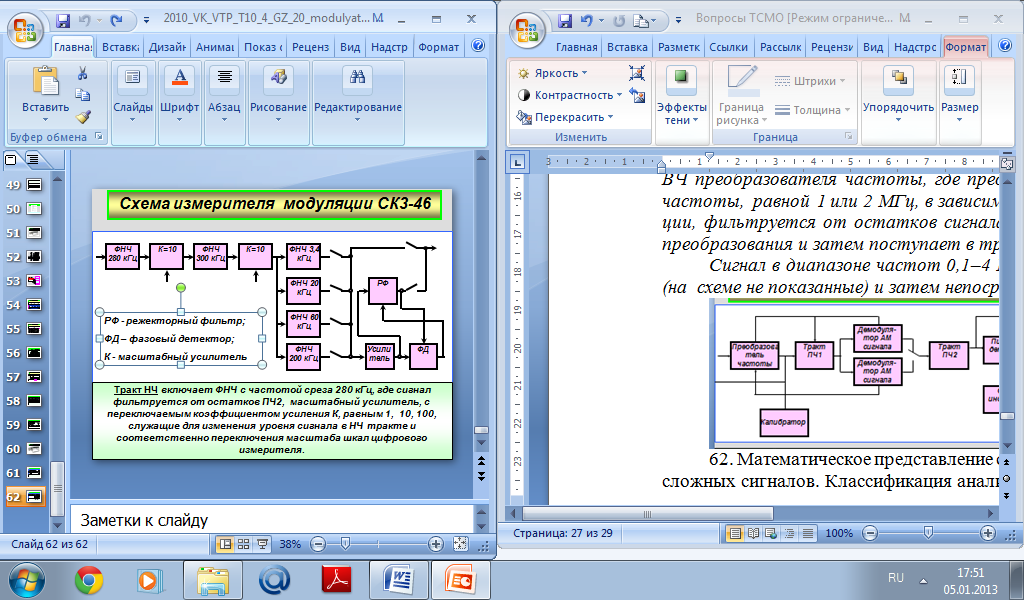
Тракт НЧ включает ФНЧ с частотой среза 280 кГц, где сигнал фильтруется от остатков ПЧ2, масштабный усилитель, с переключаемым коэффициентом усиления К, равным 1, 10, 100, служащие для изменения уровня сигнала в НЧ тракте и соответственно переключения масштаба шкал цифрового измерителя.

62. Математическое представление спектра сигналов. Спектры простых и сложных сигналов. Классификация анализаторов спектра.

В теории сигналов широкое применение нашли два способа математического и физического представ-ления электрических сигналов:

временное (обратное преобразование Фурье) и спектральное (прямое преобразование Фурье).

При временном способе анализа сигнал отражается непрерывной функцией времени или совокупностью элементарных импульсов

Спектральный способ основан на представлении (аппроксимации, декомпозиции) сигнала в виде суммы гармонических составляющих разных, обычно кратных друг другу частот

Для периодических сигналов Фурье ввел разложение по различным видам рядов — тригонометрическим, комплексным.

Любое изменение во времени некоторой периодической функции можно представить в виде конечной или бесконечной суммы ряда гармонических колебаний с разными амплитудами, частотами и начальными фазами» Фурье

а - сложное колебание;

б, в - первый и второй суммируемые сигналы

Тригонометрический ряд Фурье:

где w₁ = 2p/T - частота повторения (1-ой гармоники);

n - номер гармоники;

w_n= nw₁ (n =1, 2, …) – частоты гармоник кратные основной частоте w_1. Шаг между частотами: D w = w₁

а₀ – это среднее значение сигнала за период.

Амплитуды гармоник a_n и b_n называются коэффициентами Фурье, определяемыми интегральными выражениями:

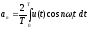
Общее представление тригонометрического ряда Фурье:

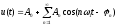
Здесь амплитуды А_n гармоник определяются выражениями:

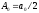
Вычисление коэффициентов Фурье a_n и b_n гармоник ряда Фурье называют гармоническим анализом.

Вычисление амплитуд А₀, А_n и фаз j_n гармоник ряда Фурье называют спектральным анализом.

Вычисление функции u(t) (1.1) путём суммирования её гармонических составляющих называют гармоническим синтезом.

Получение функции u(t) (1.2) путём суммирования её гармонических составляющих называют спектральным синтезом.

Спектр

периодической

функции

называется

линейчатым,

дискретным,

гармоническим

Комплексная форма ряда Фурье:

Комплексная форма ряда Фурье:

Формула (1.4) позволяет найти спектр периодической функции u(t) и называется прямым преобразованием Фурье.

Формула (1.3) позволяет вычислить функцию u(t) и называется обратным преобразованием Фурье.

АЧС в компл. форме

ФЧС в компл. форме

Линии, соединяющие вершины составляющих АЧС и ФЧС, называются огибающими АЧС и ФЧС.

АЧС в компл. форме

ФЧС в компл. форме

Огибающая АЧС и ФЧС тригонометрического ряда:

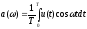
Огибающая АЧС и ФЧС комплексного ряда:

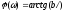
где A(w) - огибающая АЧС; j(w) - огибающая ФЧС;

w - текущая частота

Спектры случайных сигналов:

Непериодические сигналы так же, как и периодические, анализируются с помощью частотного представления. Однако для этих сигналов не могут быть использованы рассмотренные выше коэффициенты ряда Фурье a_n, b_n, A_n, j_n , так как “период” T стремится к бесконечности.

Для представления непериодических сигналов в частотной области используют интегральное преобразование Фурье.

Непериодический сигнал в виде импульса конечной длительности мысленно дополняют такими же сигналами, периодически следующими через некоторый произвольный интервал времени T = t₂ - t₁, и получают периодическую последовательность u_T(t), которая может быть представлена в виде комплексного ряда Фурье.

Одиночный сигнал и воображаемая периодическая последовательность

Примеры непериодических сигналов и их спектров:

а – экспоненциальный, б – затухающий колебательный,

в – прямоугольный

ля построения АЧС и ФЧС периодического сигнала той же формы достаточно построить огибающие и провести линии, соответствующие частотам составляющих:

а) АЧХ и ФЧХ непериодического сигнала;

б) АЧС и ФЧС периодического сигнала

Графическое представление сигнала

а — временная диаграмма; б — спектр

Анализ спектра включает измерение

как амплитуд гармоник — спектр амплитуд,

так и их начальных фаз — спектр фаз.

Амплитудно-частотный спектр последовательности радиоимпульсов

Амплитудно-частотный спектр одиночного радиоимпульса

Задачей спектрального анализа является:

- оценка формы спектра;

- измерение амплитуд гармоник;

- измерение ширины основного лепестка.

Автоматическое представление спектра сигналов осуществляется специальными приборами — анализаторами спектра.

Анализаторы спектра электрических сигналов можно классифицировать по ряду специфических признаков:

- по способу анализа — последовательные, параллельные (одновременные) и смешанные;

- по типу индикаторного устройства — осциллографические, с самописцем;

- по диапазону частот – НЧ, ВЧ, СВЧ, широкодиапазон.;

- по способу реализации – фильтровые (вида СК4), дисперсионные (вида С4).

Все эти приборы можно условно разделить на аналоговые и цифровые

Основные метрологические характеристиками анализаторов:

разрешающая способность Df_p ,

время анализа T_a и

погрешности измерения частоты и амплитуды d_f , d_A .

Для спектрального анализа непериодических сигналов используют аппарат интегрального преобразования Фурье:

При реальных измерениях наблюдают процессы на конечном интервале времени Т_a (времени анализа, наблюдения), т.е. не закончившиеся во времени:

Необходимо, чтобы T_а >> Т (Т - период следования )

63. Анализ спектра методом фильтрации.

Практически во всех аналоговых анализаторах спектра (вида СК4-...) используется фильтровый метод анализа

Аналоговые анализаторы выделяют гармонические составляющие сигнала с помощью узкополосных фильтров.

В зависимости от размещения фильтров различают:

параллельный и

последовательный анализ сигнала.

Параллельный анализ спектра:

Полоса Df_{ф i} определяет статическую разрешающую способность анализатора

Df_р — способность различать составляющие спектра с близкими частотами.

Чем уже полоса пропускания фильтра, тем выше разрешающая способность

При идеальной прямоугольной АЧХ фильтра: Df_р = Df_{фi .}

Для реальных фильтров:

Df_р =2×Df_фi

Последовательный анализ спектра :

В АС последовательного действия осуществляется перемещение по шкале всего спектра сигнала относите-льно фиксированной резонансной частоты фильтра - f_{ф 0i}

Реализация этого способа осуществляется с помощью:

1) одного полосового фильтра путём перестройки его резонансной частоты f_ф0i . В основе устройства, реализующего данный метод, лежит перестраиваемый фильтр;

2) путём преобразования частоты входного сигнала, при котором в полосу пропускания Ф по очереди попадают спектральные составляющие с различными частотами. В основе устройства, реализующего данный метод, лежит гетеродинный преобразователь частоты (автоматически перестраиваемый полосовой фильтр).

Последовательный способ анализа спектра возможен только для периодического сигнала, т.к. для выделения каждой из спектральной линий, требуется сохранение свойств сигнала во времени

1 способ:

АС с перестраиваемым фильтром (в настоящее время не применяют из-за низкой точности измерений )

2 способ:

АС с гетеродинным преобразованием

Разрешение: Т_р = Т_а Т_а – время анализа

Смеситель состоит из нелинейного элемента и колебательного контура (фильтра), резонансная частота которого соответствует промежуточной частоте, равной разности между частотой сигнала и

частотой гетеродина, образующейся

на выходе нелинейного элемента:

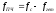
Частота на выходе ГКЧ f_гет меняется от f_min до f_max в такт с изменением напряжения генератора развертки.Разрешающая способность АС Df_p определяется полосой пропускания УПЧ.

С выхода УПЧ радиоимпульсы подаются на амплитудный детектор. С выхода детектора видеоимпульсы и_д, поступают через усилитель на вертикально отклоняющие пластины ЭЛТ. На горизонтально отклоняющие пластины ЭЛТ подается пилообразное напряжение генератора развертки, в результате чего на экране осциллографа появляются видеоимпульсы, изображающие спектр исследуемого сигнала в течение одного периода развертки: Т_р = Т_а.

Спектральный анализ гармонического сигнала в АС:

а — изменение частоты ГКЧ;

б — исследуемый спектр и АЧХ УПЧ;

в — линейное изменение

частоты во времени;

г — сигнал на выходе УПЧ;

д — сигнал на выходе детектора

Разрешающая способность АС:

Статическая разрешающая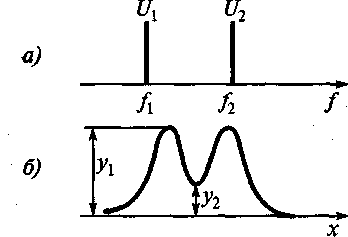

способность АС: Df_р =

а — спектр сигнала;

б — эпюры спектров на экране

Динамическая разрешающая способность АС зависит от скорости перестройки частоты ГКЧ. При увеличении скорости напряжение на выходе УПЧ не успевает изменяться с изменением напряжения на входе.

Существующие АС обеспечивают:

- работу в диапазоне f_c от 10 Гц до 40 ГГц;

- разрешающую способность Df_р = 1 кГц;

- погрешности измерения амплитуды d_A = 5%

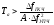гдеDf_ГКЧ»f_max…f_min;

А - коэффициент, определяемый схемой УПЧ и допустимыми динамическими погрешностями