13.Стандарт ieee 754.
Рекомендуемый для всех ВМ формат представления чисел с плавающей запятой определен стандартом IEEE 754. Этот стандарт был разработан с целью облегчить перенос программ с одного процессора на другие и нашел широкое применение практически во всех процессорах и арифметических сопроцессорах.
Стандарт определяет 32-битовый (одинарный) и 64-битовый (двойной) форматы, с 8- и 11- разрядным порядком соответственно.
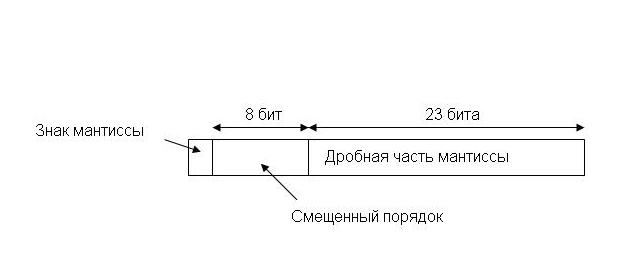
В дополнение, стандарт предусматривает два расширенных формата, одинарный и двойной, фактический вид которых зависит от конкретной реализации. Расширенные форматы предусматривают дополнительные биты для порядка (увеличенный диапазон) и мантиссы (повышенная точность).
Не все кодовые комбинации в форматах IEEE интерпретируются обычным путем — некоторые комбинации используются для представления специальных значений. Предельные значения порядка, содержащие все нули (0) и все единицы (255 — в одинарном формате и 2047 — в двойном формате), определяют специальные значения.
Параметры форматов, регламентированные стандартом IEEE 754
|
Параметр |
Формат | |||
|
|
Обычная точность |
Расширенный обычной точности |
Удвоенная точность |
Расширенный удвоенной точности |
|
Размер слова |
32 |
>=43 |
64 |
>=79 |
|
Поле порядка |
8 |
>=11 |
11 |
>=15 |
|
Смещение порядка |
127 |
не определено |
1023 |
|
|
Макс порядок |
127 |
>=1023 |
1023 |
>=16382 |
|
Миним порядок |
-126 |
<=-1023 |
-1022 |
<=-16382 |
|
Диапазон представления |
10^(-38), 10^(38) |
не определено |
10^(-308),10^(308) |
не определено |
|
Поле мантиссы |
23 |
>=31 |
52 |
>=63 |
|
Количество значений порядка |
254 |
не определено |
2046 |
не определено |
|
Количество значений мантиссы |
2^23 |
не определено |
2^52 |
не определено |
|
Количество отличающихся представимых величин |
1,98*2^31 |
не определено |
1,99*2^63 |
не определено |
Представлены следующие классы чисел:
- Порядки в диапазоне от 1 до 254 для одинарного формата и от 1 до 2036 — для двойного формата, используются для представления ненулевых нормализованных чисел. Порядки смещены так, что их диапазон составляет от -126 до +127 для одинарного формата и от -1022 до +1023 - для двойного формата. Нормализованное число требует, чтобы слева от двоичной запятой был единичный бит. Этот бит подразумевается, благодаря чему обеспечивается эффективная ширина мантиссы, равная 24 битам для одинарного и 53 битам — для двойного форматов.
- Нулевой порядок совместно с нулевой мантиссой представляют положительный или
отрицательный 0, в зависимости от состояния бита знака мантиссы.
- Порядок, содержащий единицы во всех разрядах, совокупно с нулевой мантиссой представляют положительную или отрицательную бесконечность, в зависимости от состояния бита знака, что позволяет пользователю самому решить, считать ли это ошибкой или продолжать вычисления со значением, равным бесконечности.
- Нулевой порядок в сочетании с ненулевой мантиссой представляют ненормализованное число. В этом случае бит слева от двоичной точки равен 0 и фактический порядок равен -126 или -1022. Число является положительным или отрицательным в зависимости от значения знакового бита.
- Кодовая комбинация, в которой порядок содержит все единицы, а мантисса не равна 0, используется как признак «не числа» (NAN — Not a Number) и служит для предупреждения о различных исключительных ситуациях.