Оглавление

ВВЕДЕНИЕ 2

1.ТЕОРИЯ ЛИНЕЙНОГО ОБНАРУЖЕНИЯ 2

1.1. Проверка статистических гипотез 2

1.2.Лемма Неймана-Пирсона 5

1.3. Согласованная фильтрация 9

1.4. Рабочая характеристика 12

2.ГЕНЕРИРОВАНИЕ ШУМА МЕТОДОМ СКОЛЬЗЯЩЕГО СУММИРОВАНИЯ 18

2.1. Уравнение генератора 18

Список литературы 20

Введение

Теория линейного обнаружения импульсного сигнала в аддитивном гауссовом шуме хорошо разработана [1], [2]. Теория импульсного обнаружения сигнала базируется на лемме Неймана-Пирсона, потому что в соответствии с ней отношение правдоподобия обеспечивает минимальную величину вероятности пропуска сигнала (максимальную вероятность правильного обнаружения) при условии, что вероятность ложной тревоги не превышает заданной величины. Окончательной характеристикой обнаружителя является его рабочая характеристика.

Любое устройство моделируется с помощью вычислительной техники. Для того, чтобы построить модель линейного обнаружителя необходимо построить генератор шума и записать в виде программы алгоритм обнаружения. Известны три способа генерирования шума:

1. метод скользящего суммирования;

2. метод рекуррентных разностных уравнений;

3. метод сингулярного разложения корреляционной матрицы.

Возникает вопрос о точности моделирования с использованием того или много метода генерирования шума.

Целью работы является необходимость исследовать вопрос о погрешностях моделирования с использованием генерирования шума методом скользящего суммирования.

1. ТЕОРИЯ ЛИНЕЙНОГО ОБНАРУЖЕНИЯ

   1. Проверка статистических гипотез

В математической статистике задача обнаружения сигнала формулируется как проверка гипотезы H₀против гипотезыH₁:

,

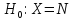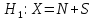
где, 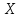— сигнал на входе,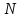— шумовая составляющая сигнала,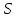— полезный информационный сигнал.

Если известны функции корреляции шума, форма, амплитуда, время прихода и длительность сигнала T, то гипотезы называются простыми: неизвестно лишь, была ли на входе сумма сигнала и шума или наблюдался только шум (рис. 1):

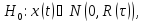
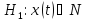
где 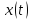– сигнал на входе;– функция корреляции.

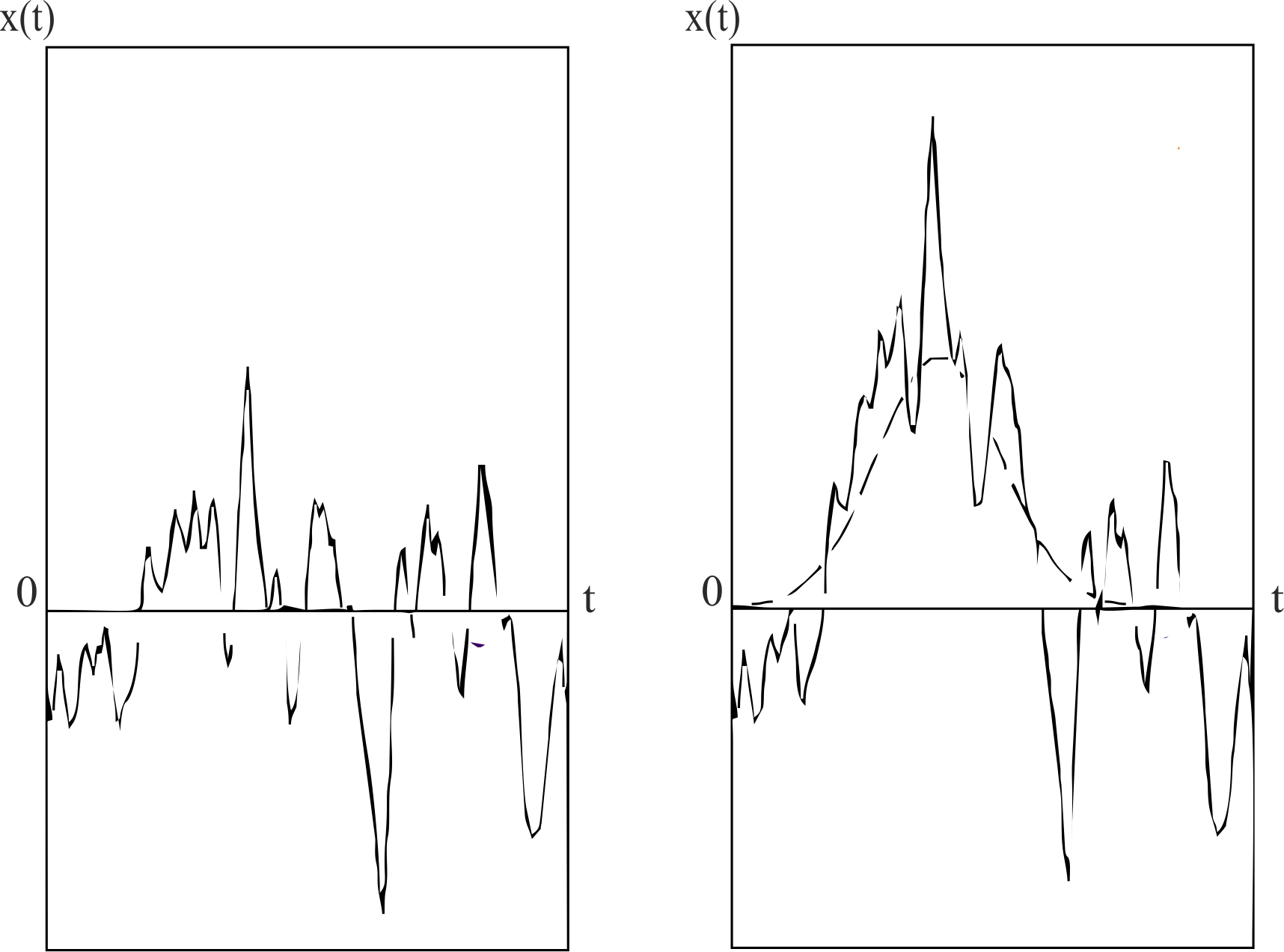
Рис. 1. – Реализации гипотез H₀,H₁

Как и любая задача математической статистики, задача проверки гипотез решается поиском оптимальной для данной задачи статистики:

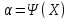(1)

Пусть статистика (1) получена в простейшей форме – в виде случайного числа.

Статистическая теория принятия решений исходит из следующих положений:

1. сигнал подлежащий обнаружению, появляется всегда на фоне шума, уровень которого случайно меняется во времени;

2. поскольку эти два процесса являются случайными, они могут быть представлены кривыми нормального распределения;

3. чтобы получить результат действия полезного сигнала, подлежащего обнаружению, надо сложить распределение эффектов, производимых только фоновым шумом и только одним сигналом (поскольку сигнал никогда не может появится без шума).

Эти положения дают возможность определить два нормальных распределения:

а) распределение эффектов одного фонового шума;

б) распределение эффектов суммы полезного сигнала и фонового шума.

Поскольку два влияния (сигнал и шум) суммируются следовательно их можно изобразить в одних и тех же координатах (см. рис. 1).

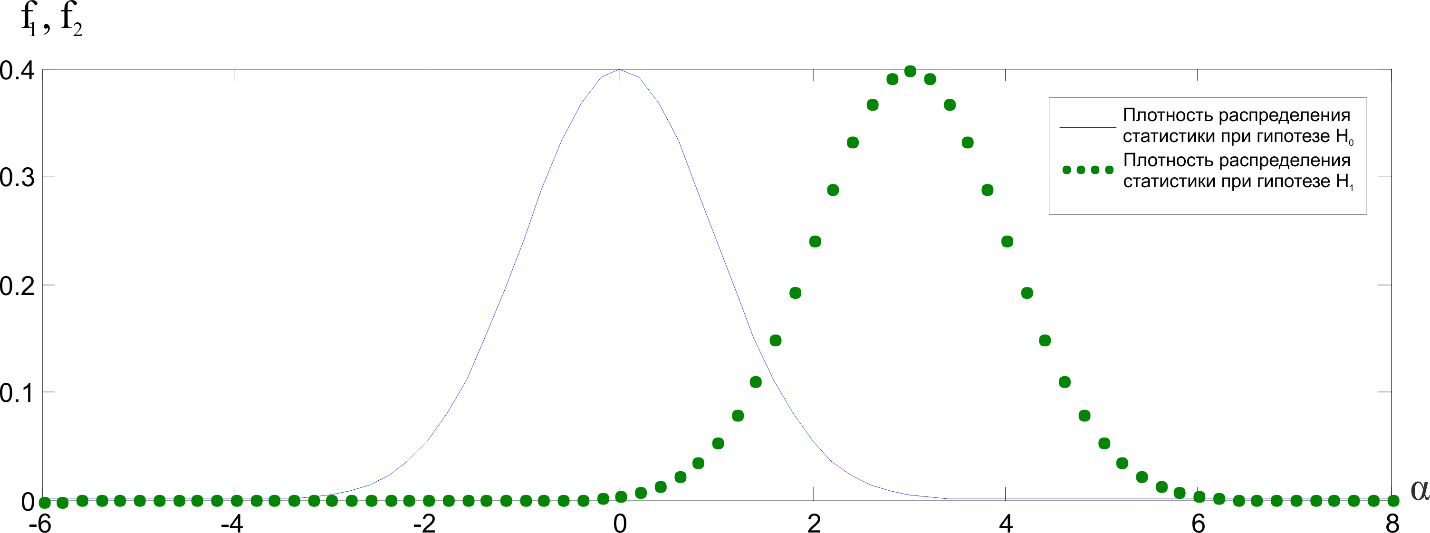
Рис. 2. — Плотности распределения

Отношение сигнал/шум — безразмерная величина, равная отношению мощности полезного сигнала к мощности шума, определяется по формуле:

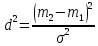
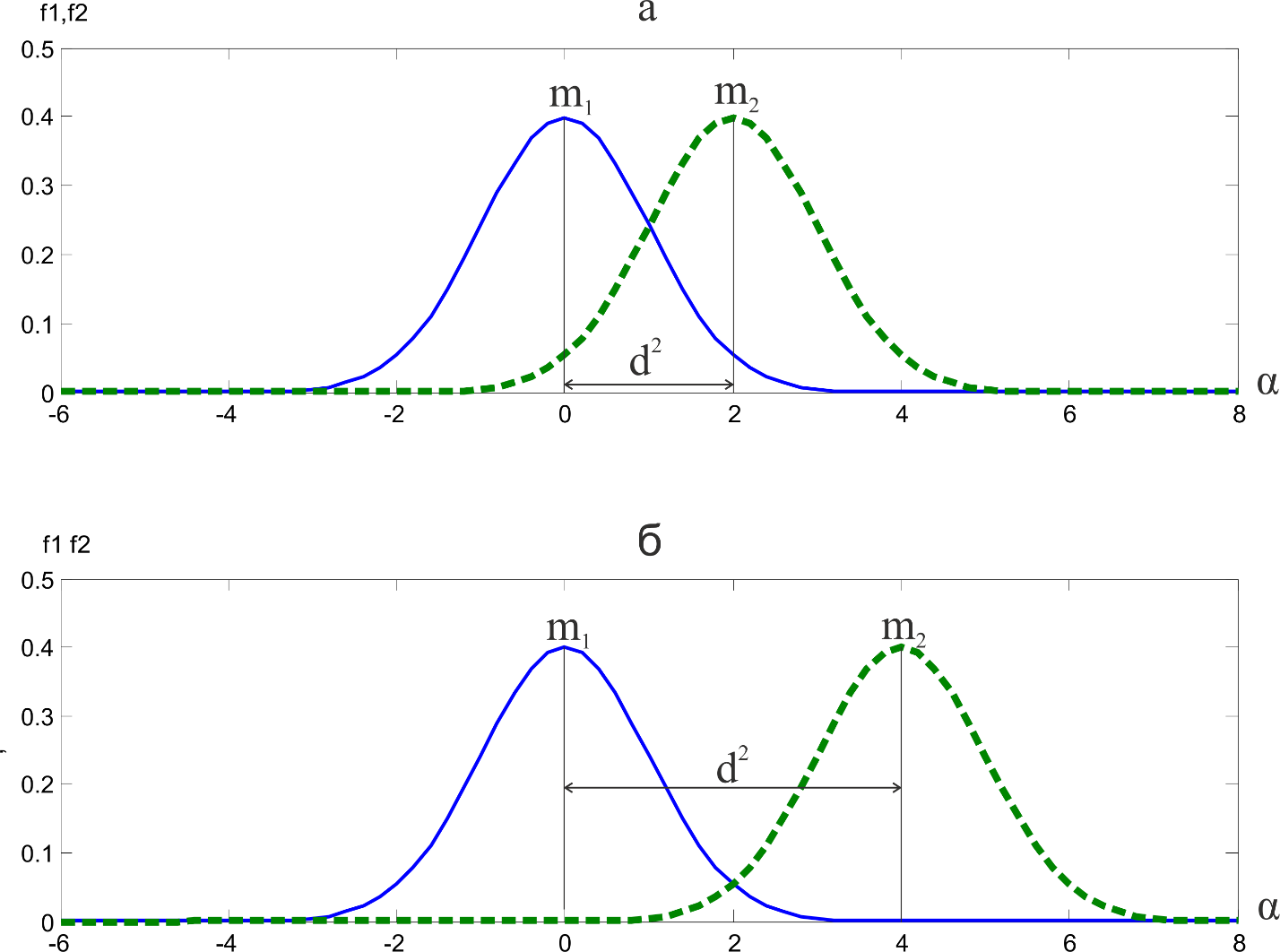
Рис. 3 — Отношение сигнал/шум

Отношение сигнал/шум — один из важнейших факторов, определяющих качество работы любой радиотехнической системы. В задачах по обнаружению сигнала необходимо принять решение: была ли на входе смесь сигнала и шума или наблюдался только шум. Кривые пересекаются следовательно принять решения легче, если отношение сигнал/шум велико (как это бывает при очень сильном сигнале рис. 3-б) , чем в том случае, когда отношение сигнал/шум имеет малые значения (рис. 3-а).

2. Лемма Неймана-Пирсона

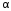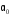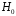Всё множество значений статистики может быть разбито значениемна области принятия решения в пользу гипотезыпри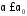или гипотезы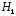при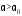(рис. 4-а).

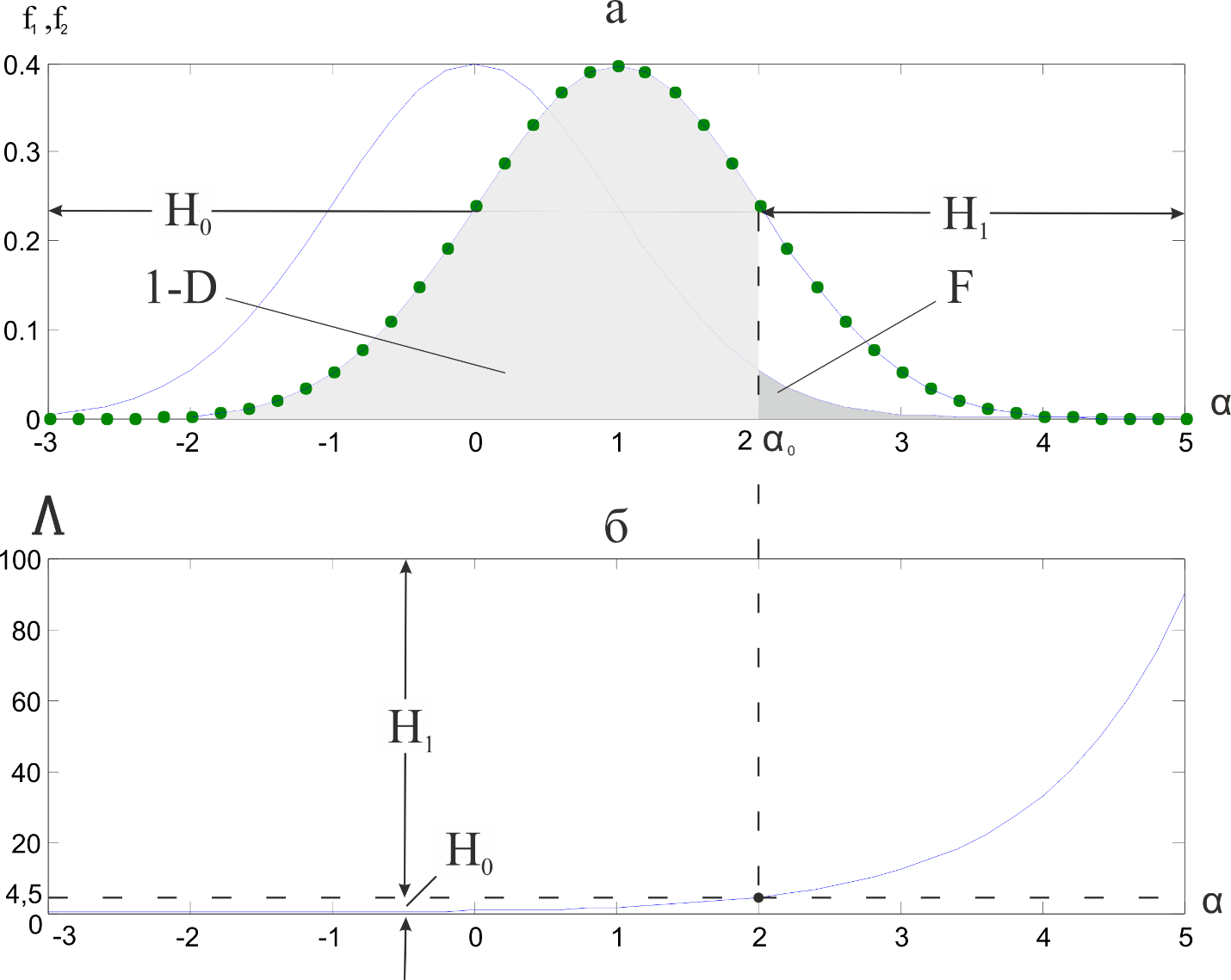
Рис. 4. — К лемме Неймана-Пирсона

Так как в общем случае плотности пересекаются, возможны ошибки принятия решений. Вероятность ошибки первого рода (гипотеза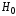отвергается, когда она верна)

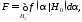(2)

вероятность ошибки второго рода (гипотеза отвергается, когда она верна)

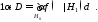(3)

В статистической радиотехнике вероятности FиDназываются соответственно вероятностьюложной тревогии вероятностьюобнаружения.

На рис. 4-а вероятности ошибок показаны заштрихованными площадями.

Пусть вероятность ложной тревоги(2) задана соответствующим выбором критического уровня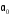. Тогда наилучшее решение задачи состоит в минимизациипропуска сигнала(ошибки второго рода) (3), или в максимизациивероятности обнаружения

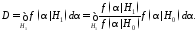
Вероятность Dмаксимальна при таком разбиении пространства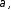чтоотношение правдоподобия

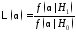(4)

максимально при условии Это записывается в виде неравенства (леммы Неймана–Пирсона)

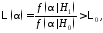(5)

- критический уровень отношения правдоподобия (рис. 4-б).

В математической статистике для проверки статистических гипотез применяется правило Неймана–Пирсона: максимизируется вероятность обнаружения Dпри фиксированной вероятности ошибки первого родаF. Правило (критерий) Неймана–Пирсона является основным и при решении задачи обнаружения в статистической радиотехнике.

Пример 1. Плотности распределения статистики изображены на рис. 4–а:

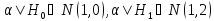
Отношение правдоподобия (4) (рис.4-б)

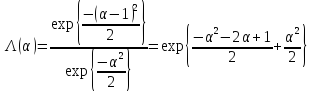
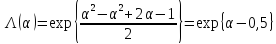
Если задать критический уровень 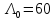то из равенства

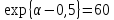
следует значение критического уровня статистики (рис. 4-а)

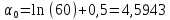
определяющее вероятности

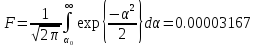
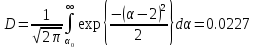
Обратно: задание вероятности F= 0,00003167 определяет критический уровень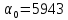что задаст единственное значение вероятностиD= 0,0227.

Разбиению пространства отношения правдоподобия на област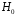и и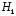принятия решения в соответствии с неравенством (5) соответствует разбиение пространства значений статистики критическим уровнем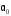(рис. 4.2).

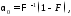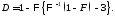В данном однопороговом примере значения вероятностей FиDсвязаны функционально, поэтому максимизация вероятностиDневозможна: заданная вероятностьFоднозначно определяет значениекоторое также однозначно задаёт вероятностьПравило Неймана–Пирсона в таком случае выглядит вырожденным. Если же задача имеет двухпороговое решение, правило Неймана–Пирсона применяется в полном объёме.