Глава 4. Имитационное моделироание исследуемой системы
По своему содержанию данная глава отражает общие результаты исследований лазерного излучения.
Нормальное распределение, также называемое распределением Гаусса - распределение вероятностей, которое в одномерном случае задается функцией плотности распределения:
(3)
где параметр μ - математическое ожидание, медиана и мода распределения, а параметр σ - стандартное отклонение(σ² - дисперсия) распределения.
Формула функции экспоненциального распределения :
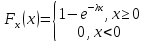(4)
Возьмем
случайные значения
с интервалом (-5;5) и построим гистограмму.
Так, математическое ожидание μ =0, объем
выборки равен 100000, а стандартное
отклонение σ=2.
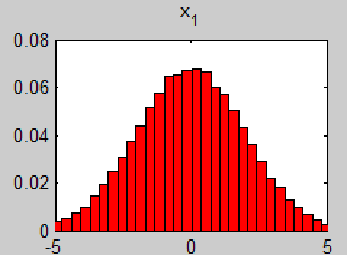
Рис.15. Гистограмма
случайных значений
на интервале (-5;5)
Так же возьмем
случайные значения
с интервалом (-5;5) и построим гистограмму.
Возьмем математическое ожидание μ =0,объем выборки равен
100000, а стандартное отклонение
σ=0.5.
Рис.16. Гистограмма
случайных значений
на интервале (-5;5)
Построим гистограмму
экспоненциальное распределение для
функции
и определим параметр λ.
Рис.17. Гистограмма
экспоненциального распределения
Проведем ещё одно
моделирование. Возьмем случайные
значения
с интервалом (-5;5) и построим гистограмму.
Так, математическое ожидание μ =1,объем
выборки равен 10000, а стандартное
отклонение σ=2.
Рис.18. Гистограмма
случайных значений
на интервале (-5;5)
Так же возьмем
случайные значения
с интервалом (-5;5) и построим гистограмму.
Возьмем математическое ожидание μ =0,объем выборки равен
10000, а стандартное отклонение
σ=0.5.
Рис.19. Гистограмма
случайных значений
на интервале (-5;5)
Рис.20. Гистограмма
экспоненциального распределения
Так же возьмем
случайные значения
с интервалом (-5;5) и построим гистограмму.
Так, математическое ожидание μ =1,объем
выборки равен 1000, а стандартное
отклонение σ=2.
Рис.21. Гистограмма
случайных значений
на интервале (-5;5)
Так же возьмем
случайные значения
с интервалом (-5;5) и построим гистограмму.
Возьмем математическое ожидание μ =0,объем выборки равен
1000, а стандартное отклонение σ=0.5.
Рис.22. Гистограмма
случайных значений
на интервале (-5;5)
Рис.23. Гистограмма
экспоненциального распределения
Возьмем случайные
значения
с интервалом (-5;5) и построим гистограмму.
Так, математическое ожидание μ =1,объем
выборки равен 500, а стандартное
отклонение σ=2.
Рис.24. Гистограмма
случайных значений
на интервале (-5;5)
Так же возьмем
случайные значения
с интервалом (-5;5) и построим гистограмму.
Возьмем математическое ожидание μ =0,объем выборки равен
500, а стандартное отклонение σ=0.5.
Рис.25. Гистограмма
случайных значений
на интервале (-5;5)
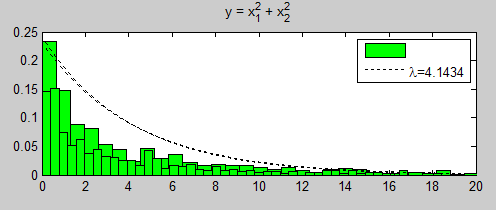
Рис.26. Гистограмма
экспоненциального распределения
4.1 Основные результаты
При исследовании были построены модели экспоненциального распределения. Так же построены разные гистограммы при разных объемах выборки. Из этих результатов видно, что объем выборки существенно влияет на сглаживание гистограммы. Так при маленьком объеме выборки гистограммы становятся изрезанными, и это говорит о том, что точность оценивания снижается при малых объемах выборки.