ekonometrika_3_var

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего профессионального образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

КАФЕДРА ЭКОНОМИКИ И ФИНАНСОВ

РУКОВОДИТЕЛЬ

доц., канд. экон. наук				Будагов А.С.
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

по дисциплине: ЭКОНОМЕТРИКА

РАБОТУ ВЫПОЛНИЛА

СТУДЕНТКА ГР.	8111				Красушкина Н.Л.
			подпись, дата		инициалы, фамилия

Санкт-Петербург

2013

Вариант №3

Обозначим через Х цену оптовой продажи некоторого товара, через Y—цену его розничной продажи.

Х	80	79	77	76	76	76	74	72	70	71	69	70
Y	84	82	81	82	81	86	83	82	82	82	82	81

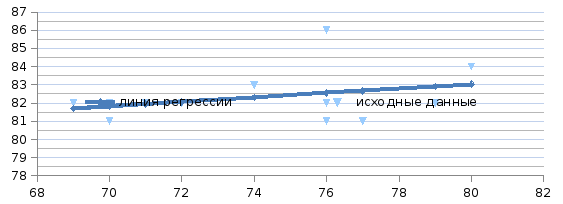
Построим поле корреляции:

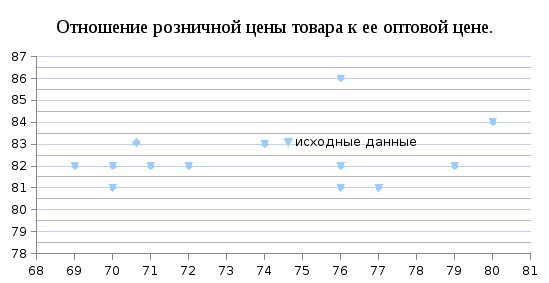
Расположение точек на диаграмме дает нам право предположить, что переменные связаны линейной зависимостью. Рассчитаем выборочные коэффициенты корреляции. Для этого проведем промежуточные вычисления, по формулам и поместим результаты вычислений в таблицу:

N	x	y	x·y	x2	y2
1	80	84	6720	6400	7056
2	79	82	6478	6241	6724
3	77	81	6237	5929	6561
4	76	82	6232	5776	6724
5	76	81	6156	5776	6561
6	76	86	6536	5776	7396
7	74	83	6142	5476	6889
8	72	82	5904	5184	6724
9	70	82	5740	4900	6724
10	71	82	5822	5041	6724
11	69	82	5658	4761	6724
12	70	81	5670	4900	6561
Σ	890	988	73295	66160	81368

Составляем систему уравнений:

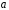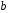
В случае линейной регрессии параметры и находятся из следующей системы нормальных уравнений МНК:

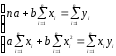
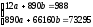
и решаем ее по формулам Крамера:

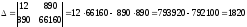
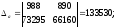
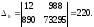
Тогда, согласно теореме Крамера,

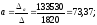
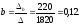
Получаем уравнение регрессии:

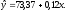
Величина коэффициента регрессии 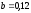означает, что увеличение оптовой цены товара на 1 ден. ед. приведет к увеличение розничной цены в среднем на 0,12 ден. ед. Коэффициент 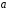в данном случае не имеет содержательной интерпретации.

3Нанесем построенную линию регрессии на диаграмму. Для этого рассчитаем значения 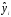, , 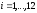по формуле:

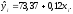
Результаты вычислений запишем в таблицу:

N	x	y	ŷt
1	80	84	83,04
2	79	82	82,92
3	77	81	82,68
4	76	82	82,55
5	76	81	82,55
6	76	86	82,55
7	74	83	82,31
8	72	82	82,07
9	70	82	81,83
10	71	82	81,95
11	69	82	81,71
12	70	81	81,83

Наносим на диаграмму точки из последнего столбца таблицы

(Линия регрессии):

Найдем величину средней ошибки аппроксимации для оценки погрешности модели, 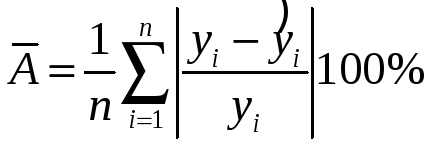. Для этого нам потребуется вычислить еще ряд промежуточных величин:

N	x	y	ŷt	y-ŷ	|(y-ŷ)/y|
1	80	84	83,04	0,96	0,01
2	79	82	82,92	-0,92	0,01
3	77	81	82,68	-1,68	0,02
4	76	82	82,55	-0,55	0,01
5	76	81	82,55	-1,55	0,02
6	76	86	82,55	3,45	0,04
7	74	83	82,31	0,69	0,01
8	72	82	82,07	-0,07	0,00
9	70	82	81,83	0,17	0,00
10	71	82	81,95	0,05	0,00
11	69	82	81,71	0,29	0,00
12	70	81	81,83	-0,83	0,01

Просуммируем теперь элементы последнего столбца и разделим полученную сумму на 12 – общее количество исходных данных:

.

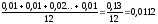Средняя ошибка аппроксимации 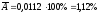. Величина ошибки оказалась около 1%, что говорит о небольшой погрешности построенной модели. Данную модель можно использовать для прогноза.

Вычислим коэффициент детерминации непосредственно по формуле:

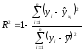
Коэффициент детерминации необходим для оценки тесноты линейной зависимости. Для его нахождения проведем ряд дополнительных вычислений.

Прежде всего, найдем выборочное среднее 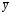по формуле:

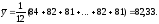
Теперь произведем расчет остальных вспомогательных величин:

N	x	y	ŷt	y-ŷ	(y-ŷ)2	y-yср	(y-yср)2
1	80	84	83,04	0,96	0,92	1,67	2,78
2	79	82	82,92	-0,92	0,84	-0,33	0,11
3	77	81	82,68	-1,68	2,81	-1,33	1,78
4	76	82	82,55	-0,55	0,31	-0,33	0,11
5	76	81	82,55	-1,55	2,42	-1,33	1,78
6	76	86	82,55	3,45	11,87	3,67	13,44
7	74	83	82,31	0,69	0,47	0,67	0,44
8	72	82	82,07	-0,07	0,01	-0,33	0,11
9	70	82	81,83	0,17	0,03	-0,33	0,11
10	71	82	81,95	0,05	0,00	-0,33	0,11
11	69	82	81,71	0,29	0,08	-0,33	0,11
12	70	81	81,83	-0,83	0,69	-1,33	1,78
Σ	890	988	988	0,00	20,45	0,00	22,67

Для вычисления коэффициента детерминации воспользуемся формулой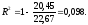

Так как 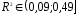, то использование регрессионной модели возможно, но после оценивания параметров модель подлежит дальнейшему многостороннему статистическому анализу.

Используя построенную модель, рассчитаем значение зависимой переменной при значении фактора 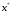, на 10% превышающего среднее значение .

Рассчитаем значение фактора, для которого необходимо построить прогноз. Для этого необходимо вычислить выборочное среднее значение 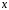по формуле:

.

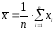Для нашей задачи среднее значение оптовой цены: .

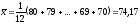Рассчитаем теперь значение .

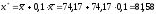Подставим теперь полученное значение фактора в уравнение регрессии и найдем прогнозируемое значение:

.

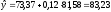Таким образом, если оптовая цена составит 81,58 ден. ед., то розничная цена составит в среднем 83,23 ден. ед.

На основании проведенного выше анализа адекватности модели можно сделать вывод о правдоподобности прогноза.

Нанесем уравнение регрессии на диаграмму, используя специальные средства Excel («Добавить линию тренда»).

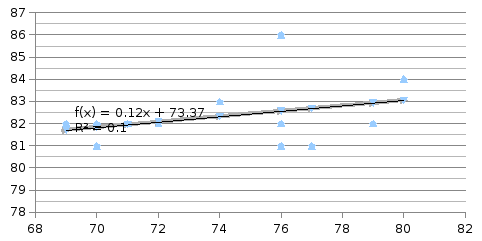
Линия регрессии, построенная нами ранее, совпала с данной линией регрессии. Нетрудно убедиться, что уравнение регрессии и коэффициент детерминации тоже совпадают с полученными ранее вручную.