Практика 2014

ГУАП

КАФЕДРА №

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЁТ О ВЫПОЛНЕНИИ ВЫЧИСЛИТЕЛЬНОЙ ПРАКТИКИ

Номер варианта: 12

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР.	4314				Логачёв Е.П.
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2014

Задание 1. Составить алгоритм действий и решить (Вариант 1)

Вариант 1: Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 1, а во второй — 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 2 камня в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 17 камней. Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.

Решение:

Игра продолжается минимум два хода, максимум

четыре. Из таблицы ясно , что второй игрок на своём втором ходу выигрывает . Если же второй игрок не выиграл ,то может выиграть первый игрок. Таким образом, при правильной игре выиграет второй игрок при любом ходе первого игрока.

Ходы	Возможные комбинации ходов
0	1 2
1	3 6	3 6	3 4	3 4	2 6	2 6
2	9 18	9 18	5 6	9 12	6 8	6 8
3			7 8		18 24	8 10
4			9 10

Ответ: При правильной игре выиграет второй игрок при любом ходе первого игрока.

Задание 2. Составить алгоритм действий и решить (Вариант 2)

Вариант 2: Два игрока играют в следующую игру. На координатной плоскости в точке с координатами (-2;-1) стоит фишка. Игроки ходят по очереди. Ход состоит в том, что игрок перемещает фишку из точки с координатами (x,y) в одну из трех точек: (x+3;y), (x,y+4) или (x+2,y+2). Выигрывает тот игрок, после хода которого расстояние по прямой от фишки до начала координат (0,0) больше 9 единиц. Кто выигрывает — игрок, делающий ход первым, или игрок, делающий ход вторым?

Решение:

1)из каждой ситуации в этой игре возможно три продолжения, поэтому дерево получается троичным

2)по теореме Пифагора расстояние L от точки с координатами (x;y) до начала координат – это квадратный корень из суммы квадратов координат:; чтобы избавиться от вычисления квадратного корня, нужно перейти от заданного условия к равносильному условию в целых числах:

3)в начальный момент, условие не выполнено

4)первый игрок имеет три варианта хода, запишем их в таблицу, указывая для каждого положения координаты (в скобках) и значение;

0		1			2			3
(x;y)		(x;y)		(x;y)			(x;y)
(-2;-1)	5	(1;-1)	2	(-2;3)		13	(0;1)		1

5)видим, что одним ходом первый игрок может выиграть сразу;

6)построим следующий столбец таблицы (ход второго игрока):

0		1 игрок			2 игрок
(x;y)		(x;y)		(x;y)
(-2;-1)	5	(-1;1)	2	(2;1)		5
				(-1;5)		26
				(1;3)		10
		(0;1)	1	(3;1)		10
				(0;5)		25
				(2;3)		13

7) второй игрок может выиграть большинстве числа ходов-

восьми из девяти;

8)предположим, что на втором ходу ещё никто не выиграл ,тогда

следует третий ход;

9) строим таблицу для третьего хода (игрок 1)

0		1 игрок		2 игрок			1 игрок
(x;y)		(x;y)		(x;y)		(x;y)
(-2;-1)	5	(-1;1)	2	(2;1)	5	(5;1)		26
						(2;5)		29
						(4;3)		25

10)как видим дальнейшая игра невозможна ,так как первый игрок выигрывает;

Из таблиц ясно , что второй игрок на своём втором ходу выигрывает

в восьми из девяти случаев .

Если же второй игрок не выиграл ,то однозначно выигрывает первый игрок.

Таким образом, при правильной игре выиграет второй игрок при любом ходе первого игрока.

Ответ: При правильной игре выиграет второй игрок при любом ходе первого игрока.

Задание 3. (Вариант 3) Написать алгоритм программы, при выполнении которой с клавиатуры считываются координаты точки на плоскости (x1,y1 – действительные числа) и определяется принадлежность точки некоторой области, включая ее границы. Область ограничена графиком y=f(x) и прямыми y= a , x=b и х=c.

Вариант 3 : f(x)=cos(x)-0.25, a=0, b=0, c=3.5.

По заданию можно судить, что для решения задачи нужно ограничить область плоскости некоторыми функциями (см. рис 1).

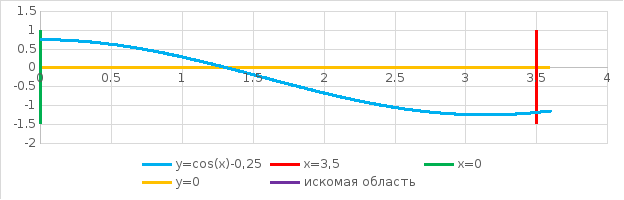
Рис. 1. График искомой области.

Для проверки попадания точки в две данные фигуры, последовательно проверим каждую из границ и в случае если все границы соблюдены мы можем быть уверены, что точка лежит в данных областях. Итак, ограничивать область сверху и снизу будет функция , левой границей – , правой – , а верхней . Теперь достаточно составить алгоритм и написать простенькую программу.

Алгоритм для выполнения задачи №3.

Текст программы на C/C++:

#include <stdio.h>

#include <math.h>

int main()

{

float x1,y1;

scanf("%f %f", &x1, &y1);

if ((x1>=0) && (x1<=3.5) && ( ((y1>=0) && (y1<=cos(x1)-0.25)) || ((y1<=0) && (y1>=cos(x1)-0.25)) ))

printf("(%.2f,%.2f) - located on given area", x1, y1);

}

Вывод: Языки программирования высокого уровня очень хорошо подходят для решения прикладных и математических задач.

Задание 4. (Вариант 4) Вывести все десятичные числа A (100<А<500), в двоичной записи которых число единиц превосходит число нулей.

Решение: Для решения данной задачи отлично подойдет один из языков программирования высокого уровня. Задача сводится к тому во время отработки рекуррентной формулы нахождения двоичного числа найти количество единиц и нулей, а проверка условия займет не более двух строк. Все это повторить используя цикл с параметром.

Алгоритм для выполнения задачи №4.

Текст программы на C/C++:

#include <stdio.h>

int main()

{

for(int i=100; i<501; i++)

{

int k=1, t=0, f=0, d=i;

while (d)

{

if((d%2)==0)

f++;

else

t++;

d/=2;

k*=10;

}

if(t>f)

printf("%3i ", i);

}

}

Вывод: Языки программирования высокого уровня очень хорошо подходят для решения прикладных и математических задач.

Задание 5. (Вариант 5) Решить логическую задачу. Примеры выполнения задания приведены в Приложении.

Вариант 5. Дина, Соня, Коля, Рома и Миша учатся в институте. Их фамилии – Бойченко, Карпенко, Лысенко, Савченко и Шевченко.  Рома никогда не видел своей мамы.  Родители Дины никогда не встречались с родителями Коли.  Студенты Шевченко и Бойченко играют в одной баскетбольной команде.  Услышав, что родители Карпенко собираются поехать в город, мать Шевченко пришла к матери Карпенко и попросила, чтобы та отпустила своего сына к ним на вечер, но оказалось, что отец Коли уже договорился с родителями Карпенко и пригласил их сына к Коле.  Отец и мать Лысенко – хорошие друзья родителей Бойченко. Все четверо очень довольны, что их дети собираются пожениться.  Установите имя и фамилию каждого из молодых людей и девушек. 

Решение:

Имеется пять утверждений:

1. Рома никогда не видел своей мамы. 

2. Родители Дины никогда не встречались с родителями Коли. 

3. Студенты Шевченко и Бойченко играют в одной баскетбольной команде. 

4. Услышав, что родители Карпенко собираются поехать в город, мать Шевченко пришла к матери Карпенко и попросила, чтобы та отпустила своего сына к ним на вечер, но оказалось, что отец Коли уже договорился с родителями Карпенко и пригласил их сына к Коле. 

5. Отец и мать Лысенко – хорошие друзья родителей Бойченко.

Составим таблицу:

Фамилии Имя	Шевченко	Карпенко	Савченко	Бойченко	Лысенко
Рома	-	-	+	-	-
Коля	-	-	-	-	+
Соня	-	-	-	+	-
Дина	+	-	-	-	-
Миша	-	+	-	-	-

Рома никогда не видел своей мамы.  Учитывая это обстоятельство, можно сделать вывод, что Рома — не Карпенко, не Шевченко, не Лысенко и не Бойченко. Следовательно, он Савченко. Отметим это в таблице. Учтём и то, что Карпенко — юноша, следовательно, он — не Дина, не Соня, и к тому же — не Коля («отец Коли уже договорился с родителями Карпенко»). Следовательно, его зовут Миша. Занесём в таблицу и этот вывод.

Как известно, в одной баскетбольной команде играют либо одни юноши, либо одни девушки. Пара «Шевченко + Бойченко» мужской быть не может, так как в качестве возможных претендентов на эти две фамилии у нас остались две девушки и один юноша. Следовательно, Шевченко и Бойченко — девушки. Значит, фамилия Коли — Лысенко. Это легко установить, взглянув на таблицу.

Остается выяснить имя и фамилию каждой из девушек. Сопоставим два факта: «Родители Дины никогда не встречались с родителями Коли (мы уже знаем, что его фамилия — Лысенко)» и «Родители Лысенко дружат с родителями Бойченко». Ясно, что Дина — не Бойченко. Следовательно, ее фамилия Шевченко, а фамилия Сони — Бойченко.

Ответ:

Рома-Савченко;

Коля-Лысенко;

Миша-Карпенко;

Соня-Бойченко;

Дина-Шевченко.

Вывод:

Развил и усовершенствовал навыки в областях теории алгоритмизации, практического решения прикладных информационных задач и использования современной вычислительной техники. Ознакомился с возможностями вычислительной лаборатории кафедры моделирования вычислительных и электронных систем.